Polygon Angles Worksheet: Master the Math Easily
Understanding the angles within polygons is a crucial aspect of geometry, especially for students who want to excel in mathematics. Whether you're preparing for an upcoming test, or you're just curious to learn more, this comprehensive guide will make mastering polygon angles straightforward and engaging. Dive into the world of polygons with us, as we explore their angles, solve problems, and enhance your mathematical abilities!
What is a Polygon?

A polygon is a plane figure that is bounded by a closed path or circuit, composed of a finite sequence of straight line segments. These segments are called the sides of the polygon, and the points where two sides meet are called polygon’s vertices or corners.
Types of Polygons

- Regular Polygons: All sides and internal angles are equal.
- Irregular Polygons: Sides and internal angles can be of different lengths and sizes.
- Convex Polygons: All interior angles are less than 180 degrees.
- Concave Polygons: At least one interior angle is greater than 180 degrees.

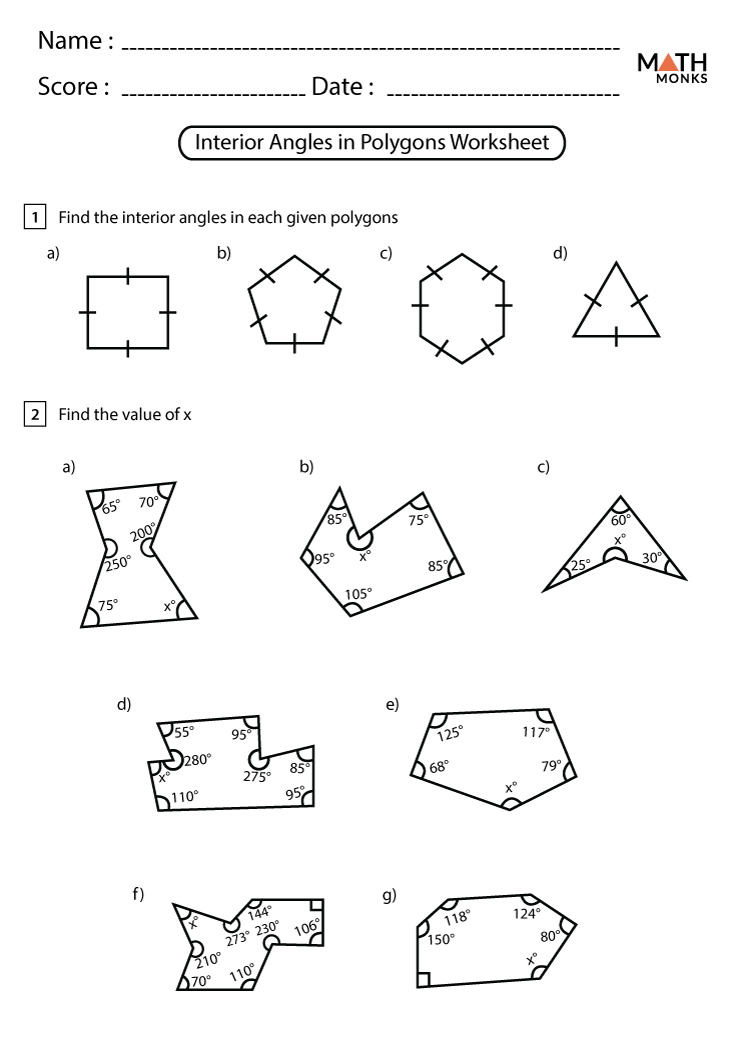
Sum of Interior Angles in Polygons

Calculating the sum of interior angles in any polygon is relatively easy. Here’s the formula:
[ \text{Sum of Interior Angles} = (n - 2) \times 180^\circ ]
where n is the number of sides of the polygon.
For instance:
- A triangle (3 sides) has a sum of 180°.
- A square or rectangle (4 sides) has a sum of 360°.
- A pentagon (5 sides) has a sum of 540°.
🔍 Note: Understanding the formula for the sum of interior angles can help with solving various geometry problems.
Calculating an Individual Interior Angle

For regular polygons, where all angles are the same, you can find the measure of one interior angle by dividing the sum by the number of sides:
[ \text{Interior Angle} = \frac{(n - 2) \times 180^\circ}{n} ]
| Number of Sides | Sum of Interior Angles | Single Interior Angle |
|---|---|---|
| 3 (Triangle) | 180° | 60° |
| 4 (Square/Rectangle) | 360° | 90° |
| 5 (Pentagon) | 540° | 108° |

💡 Note: The above formula assumes you're dealing with a regular polygon. For irregular polygons, you'll need to calculate each angle individually.
Exterior Angles

Each exterior angle of a regular polygon is simply the supplement to an interior angle:
[ \text{Exterior Angle} = \frac{360^\circ}{n} ]
This means that for any regular polygon, if you add up all the exterior angles, they will always equal 360 degrees.
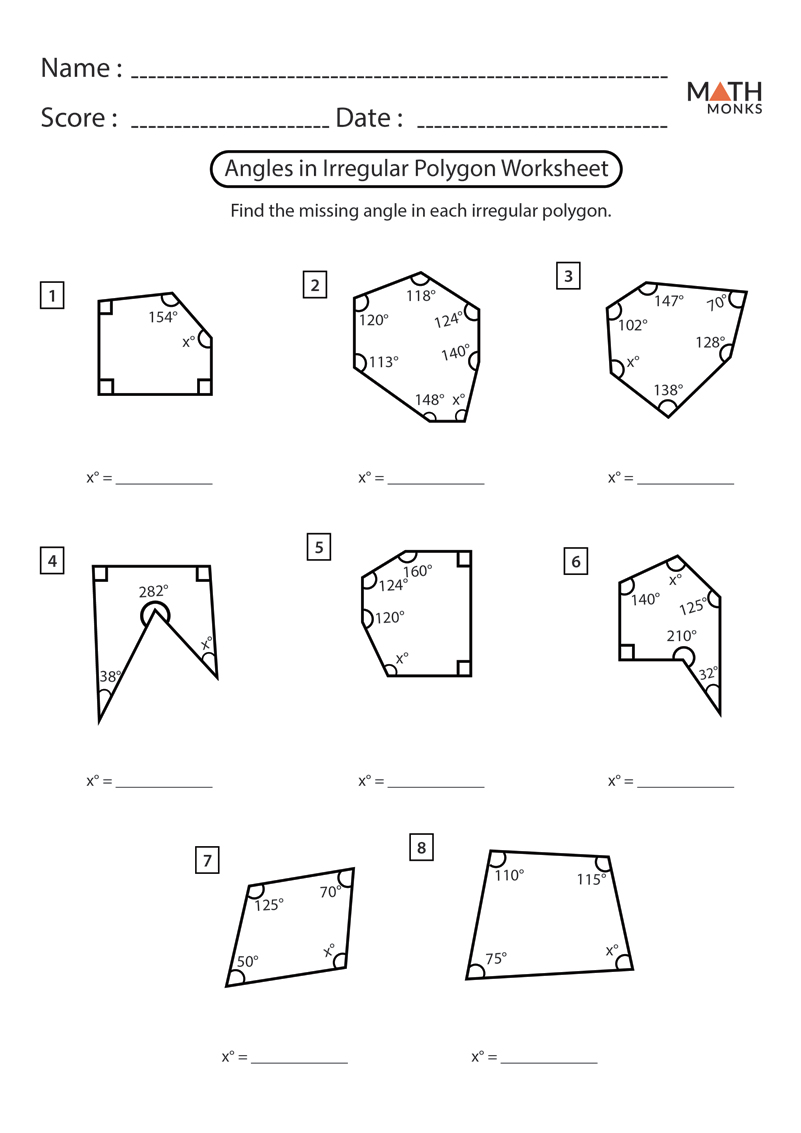
Polygon Angle Worksheet: Practical Applications

Here are some exercises to practice your understanding of polygon angles:
- Calculate the sum of the interior angles of an octagon (8 sides).
- Determine the measure of one interior angle in a regular hexagon (6 sides).
- Find the exterior angle of a regular pentagon.
📝 Note: Use a calculator or paper for solving the problems above. Remember, practice is the key to mastery!
Polygons in Real Life

Polygons aren’t just theoretical; they’re all around us:
- Architecture: Windows, doors, and floors often feature polygonal shapes.
- Design: Logos, packaging, and art designs often incorporate polygons for symmetry and aesthetics.
- Geography: Surveyors use polygons to map and describe land boundaries.

Advanced Topics

For those looking to delve deeper:
Tessellations
Polygons, particularly regular polygons, can be used to create patterns where every side of every polygon fits perfectly with another side. These are known as tessellations or tiling.
Non-Convex Polygons
Understanding the properties of non-convex polygons (with angles greater than 180°) and their relationship to other polygons can provide further mathematical challenges and insights.
In wrapping up, mastering the intricacies of polygon angles is not just about understanding the numbers; it's about seeing geometry in action all around us. From designing buildings to solving complex problems, the knowledge of polygons enhances our interaction with the world in a myriad of ways. We've covered the fundamentals, formulas, and real-world applications, ensuring that you're well-equipped to tackle any polygon-related problem with confidence. Remember, the beauty of geometry lies in its patterns, its logic, and the surprising ways it manifests in our daily lives.
What is the easiest way to remember the sum of interior angles in a polygon?

+
The easiest way to remember is to use the formula ((n - 2) \times 180^\circ) where (n) is the number of sides.
How do you identify a concave polygon?

+
Identify a concave polygon by finding at least one interior angle that is greater than 180 degrees.
What are some practical uses of knowing polygon angles?
+
Knowing polygon angles helps in areas like land surveying, architectural design, and even in video game development for creating realistic environments.