Points Lines And Planes Worksheet With Answer Key

Understanding Points, Lines, and Planes in Geometry
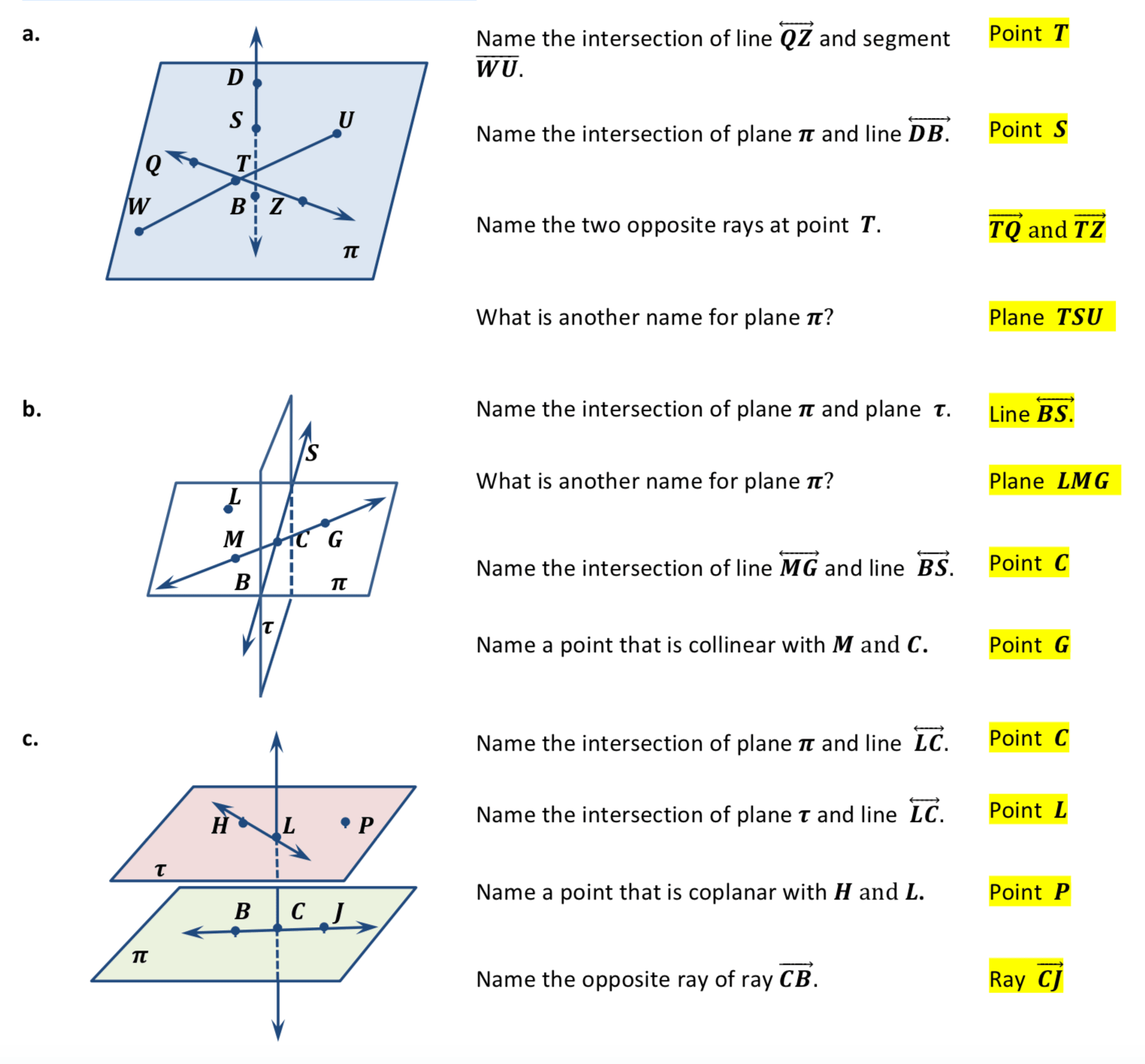
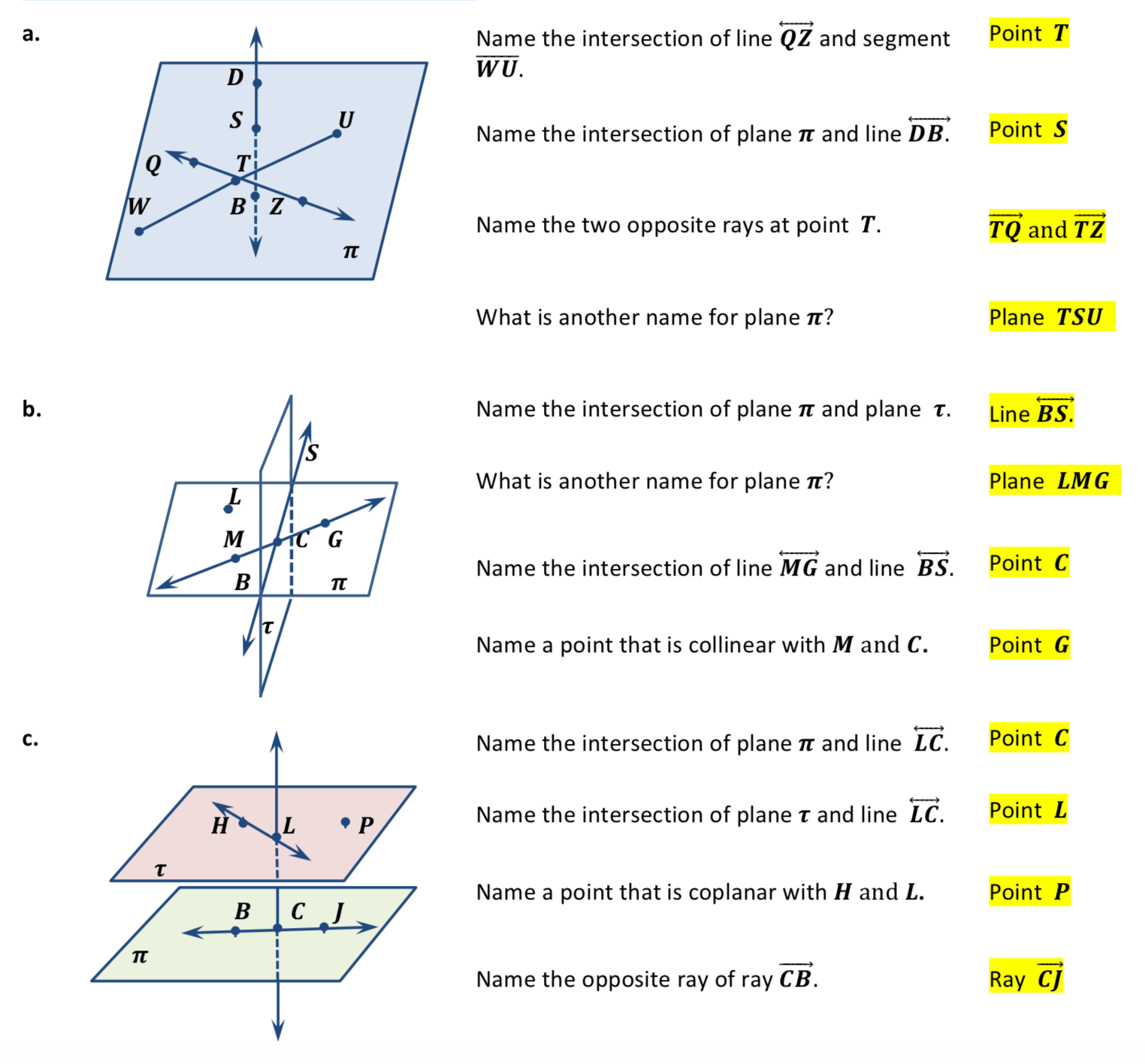
Geometry, at its core, deals with points, lines, and planes as fundamental elements. These basic concepts form the building blocks for more complex geometric shapes and theorems. In this comprehensive guide, we'll explore what points, lines, and planes are, how they interact, and how they're used in mathematical problems through a points lines and planes worksheet.
What is a Point?

A point is the most basic element in geometry, often represented by a dot on a diagram. It has no size, no dimensions, just a location in space.
- Representation: Points are typically labeled with a capital letter, like P or A.
- Key Properties: Points do not occupy any space, hence are dimensionless.
What is a Line?

A line extends infinitely in two directions. It has length but no width or depth, making it a one-dimensional geometric object.
- Representation: Lines can be drawn as arrows to show their infinite continuation or labeled with lowercase letters like l or m.
- Key Properties:
- Parallel lines never intersect.
- Intersecting lines cross at a single point.
- Perpendicular lines form a 90-degree angle.
📝 Note: Two points determine a unique line, which is known as the Line Postulate.
Understanding Planes

A plane in geometry is a flat, two-dimensional surface that extends infinitely in all directions. Think of it like a piece of paper without edges or thickness.
- Representation: Planes can be represented with a capital letter or by three points not on the same line like Plane ABC.
- Key Properties:
- Planes have infinite length and width but no thickness.
- Three noncollinear points determine a unique plane.
Interaction Between Points, Lines, and Planes

The interaction of these geometric entities can be illustrated through various problems:
- Collinear Points: Points that lie on the same line are called collinear.
- Coplanar Points: Points that lie in the same plane are coplanar.
Worksheet Problems and Solutions

Example Problem 1: Naming and Identifying

Problem: Given points A, B, C, and D which form the vertices of a quadrilateral, identify:
- A line segment connecting point A and point B.
- A plane containing point A, B, and C.
| Question | Answer |
|---|---|
| Line segment between A and B | AB or BA |
| Plane with points A, B, C | Plane ABC or Plane BAC |
Example Problem 2: Postulates and Theorems

Problem: Use the following postulates to answer:
- Through any two points, there exists exactly one line.
- If two lines intersect, they intersect in exactly one point.
Question: If point P lies on line l and point Q does not lie on line l, how many lines can be drawn through points P and Q?
Answer: Only one line can be drawn through any two points, thus there is exactly one line through P and Q.
Conclusion

In summary, the concepts of points, lines, and planes are essential to understanding the foundational principles of geometry. Through our exploration, we've learned how these elements are defined, interact with each other, and are used in practical geometric problems. Worksheets and exercises focusing on these elements not only reinforce the understanding of basic geometric principles but also enhance problem-solving skills. Remember, geometry is not just about memorizing shapes but understanding the properties and relationships between them, making it a fascinating area of mathematics.
What is the significance of points in geometry?

+
Points are fundamental to geometry as they represent locations in space. They are used to define other geometric objects like lines and planes, and are critical in establishing theorems and postulates.
How can lines and planes intersect?

+
Lines can intersect in a single point or not at all if they are parallel. Planes can intersect along a line, remain parallel, or coincide entirely if they are the same plane.
Why do we use worksheets for learning geometry?

+
Worksheets provide practical applications of geometric concepts, allowing students to test their understanding, identify points of confusion, and practice applying theorems and properties of points, lines, and planes in real-world contexts.