5 Essential Tips for Mastering Points, Lines, and Planes
The world of geometry is fascinating and complex, filled with an array of shapes and structures that form the backbone of various scientific and artistic fields. Understanding the basics like points, lines, and planes can significantly enhance your grasp of both simple and complex geometric concepts. Here, we delve into 5 essential tips to help you master these fundamental elements.
1. Start with the Basics

Before diving into the more intricate aspects of geometry, make sure you are comfortable with the very basics:
- Point: A point is a precise location in space. It has no size or dimension; it’s simply a location. Think of it as a dot on a page.
- Line: A line is an infinitely long series of points that extends in both directions without ending. It can be thought of as a straight thread or string with no thickness.
- Plane: A plane is a flat, two-dimensional surface that extends infinitely in all directions. Imagine a piece of paper that has no edges or thickness.
These definitions might sound straightforward, but fully understanding their implications can lead to deeper geometric insights.
2. Visualize with Drawing and Modeling
Visualization is a powerful tool in geometry. Here are some tips to enhance your visual understanding:
- Use drawing tools like compasses, straightedges, or even digital tools to create points, lines, and planes. Drawing helps in visualizing geometric concepts more concretely.
- Create models: Using clay, cardboard, or 3D software, you can model planes and lines to see how they interact in space. This hands-on approach reinforces theoretical learning.
- Explore different angles: Try sketching or modeling the same geometric configurations from various perspectives to understand the spatial relationships better.

🔍 Note: Remember that accuracy in drawing is key. Small errors in sketching can lead to significant misinterpretations in understanding.
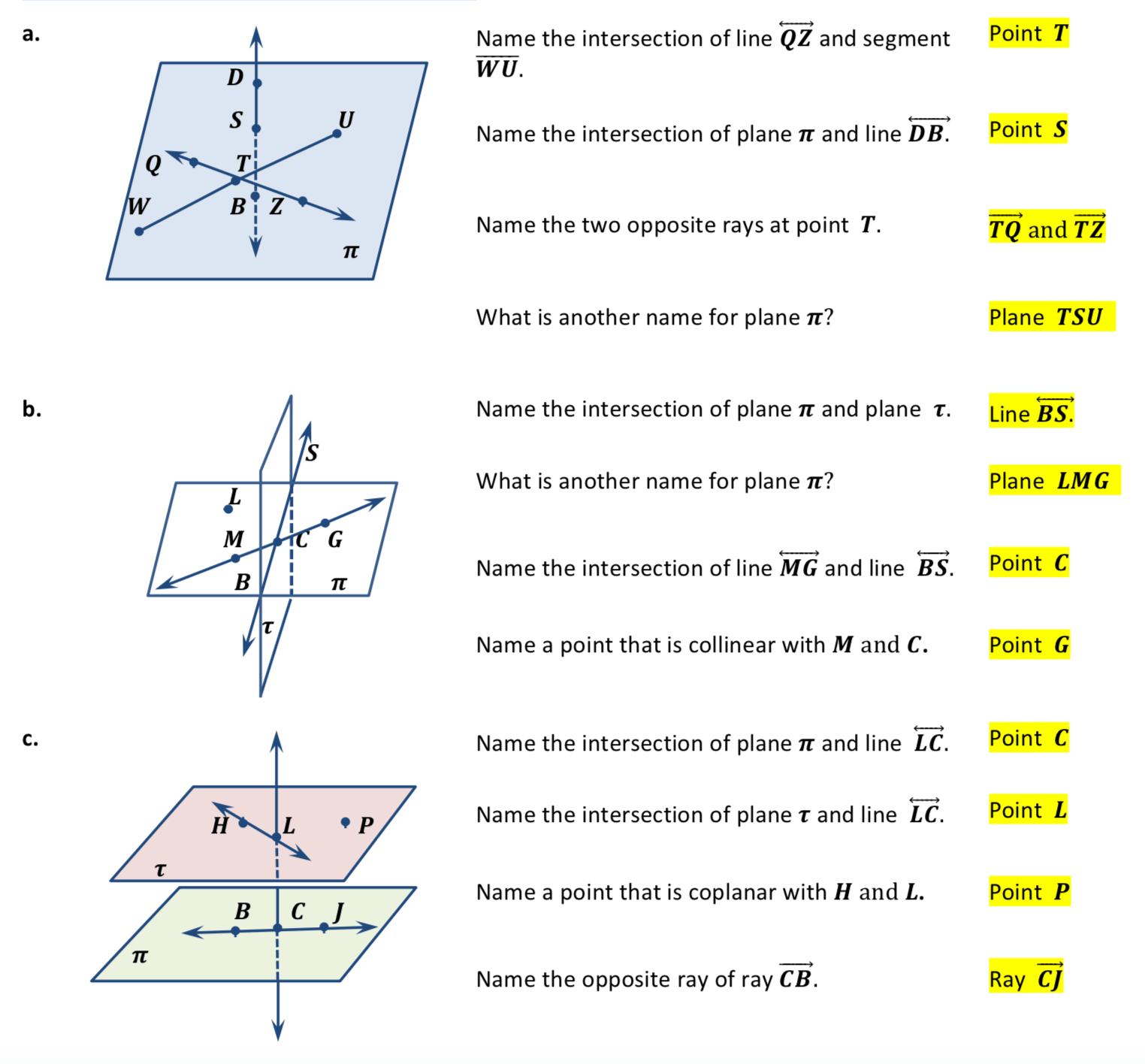
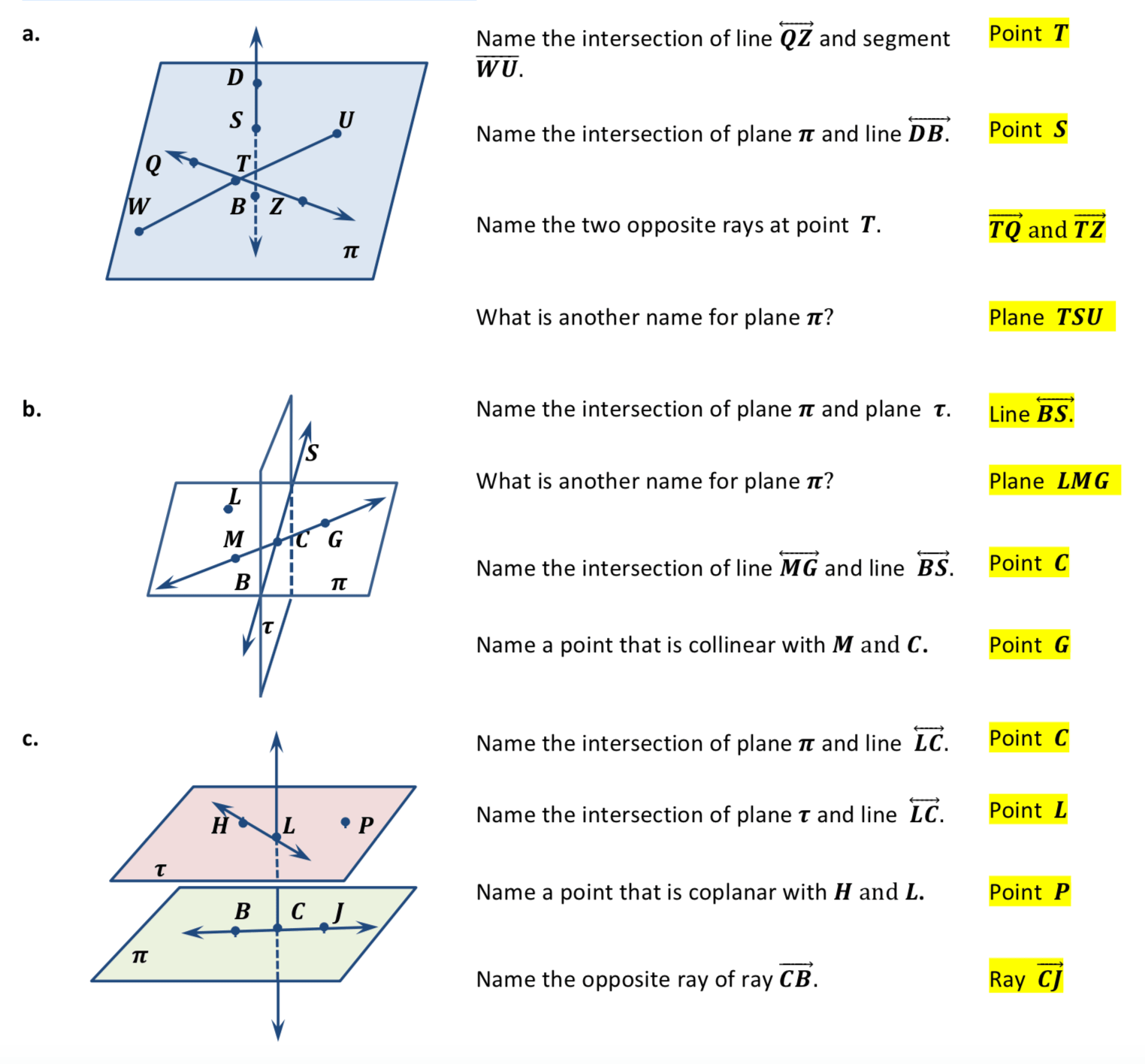
3. Understand the Intersections

How points, lines, and planes intersect each other is crucial for advanced geometric problem-solving:
- Line Intersection: Two lines can either intersect at one point or not intersect at all if they are parallel.
- Line and Plane Intersection: A line can intersect a plane at a single point, lie entirely within the plane, or be parallel to the plane.
- Plane Intersection: The intersection of two planes forms a line, while the intersection of three or more planes can be a line or a point or nothing at all if the planes are not positioned correctly.
| Element | Intersects With | Result |
|---|---|---|
| Line | Line | Point or no intersection |
| Line | Plane | Point, line, or no intersection |
| Plane | Plane | Line, Point, or no intersection |

🌐 Note: Understanding these intersections helps in solving problems involving angles, perpendicularity, and parallelism.
4. Use Algebraic Methods
Geometry isn't just about drawing or modeling; algebraic methods can provide precise solutions:
- Equation of a Line: Use the slope-intercept form (y = mx + b) to represent lines algebraically. This helps in calculating intersections and understanding geometric properties.
- Equation of a Plane: Planes can be described by linear equations in three variables (Ax + By + Cz = D). This algebraic approach is essential for problems involving three dimensions.
- Analyze geometric configurations through algebraic tools like matrices, which are particularly useful in linear transformations and vector analysis.
Here’s how you might represent points, lines, and planes in algebraic terms:
y = 2x + 3 # (y = mx + b)
3x + 2y - z = 1 # (Ax + By + Cz = D)
📝 Note: Algebraic manipulation can often simplify complex geometric problems, offering insights that might not be apparent visually.
5. Practice with Real-World Applications

Geometry is not just an academic subject; it's deeply embedded in our daily lives:
- Architecture and Engineering: From designing buildings to planning urban layouts, geometric principles are everywhere. Understanding points, lines, and planes helps in visualizing structures in 3D space.
- Art and Design: Artists use geometry to create perspective, proportion, and balance in their works. Whether it’s painting, sculpture, or digital art, geometric fundamentals are crucial.
- Computer Graphics: 3D modeling, video games, and animation heavily rely on geometric calculations to render scenes accurately.
By recognizing these applications, you can relate abstract geometric concepts to tangible, real-world scenarios:
- Look at the symmetry in nature or man-made structures.
- Analyze how shadows and lines create different shapes in everyday life.
- Explore how perspective drawings use lines converging to vanishing points to create a sense of depth.
In summary, mastering points, lines, and planes involves:
- Understanding their basic definitions.
- Enhancing visualization skills through drawing and modeling.
- Grasping how these elements intersect with each other.
- Using algebraic methods to solve geometric problems.
- Relating geometric concepts to real-world scenarios for practical application.
This holistic approach not only makes learning geometry more engaging but also significantly improves your problem-solving capabilities in various fields. Whether you're a student, an artist, an engineer, or simply someone intrigued by the beauty of mathematics, these tips will help you navigate through the geometric landscape with confidence and creativity.
What is the importance of understanding points, lines, and planes in daily life?
+
Understanding points, lines, and planes helps in solving practical problems in design, engineering, architecture, and various forms of art, thereby influencing how we perceive and interact with our environment.
How can I improve my visualization of geometric shapes?

+
Regular drawing, modeling, and using different media like clay, software, or even sketches from various angles can enhance your visualization skills. Additionally, exploring geometry through interactive tools can also be helpful.
Why do we need algebra in geometry?
+
Algebra provides precise tools to describe and analyze geometric shapes and their relationships. Equations help in defining lines and planes, solving for intersections, and understanding geometric transformations.