5 Essential Tips for Point Slope Form Worksheet Kuta

In the vast landscape of mathematics, where equations of lines traverse through coordinate planes like roads on a map, understanding how to express these lines in various forms is crucial. Among these forms, point-slope form stands out as both intuitive and widely applicable. For educators and learners seeking to enhance their grasp on this topic, worksheets like those provided by Kuta Software offer a structured approach to mastering this concept. Here, we delve into five essential tips to effectively use Point Slope Form worksheets from Kuta Software.
Understanding the Basics


Before diving into the worksheet, it’s beneficial to review the fundamentals:
- The point-slope form of a line is expressed as y - y₁ = m(x - x₁), where (x₁, y₁) are coordinates of a known point on the line, and m is the slope.
- This form allows you to write an equation of a line when you know a point on the line and its slope.
- It’s especially useful in real-world applications where you might need to find the equation of a line given initial conditions.
Tip 1: Start with Conceptual Understanding

Before working through the exercises in your Kuta Software worksheet, ensure that you grasp the conceptual underpinnings of point-slope form:
- Understand how to derive the equation from geometric principles or physical scenarios.
- Appreciate the flexibility of point-slope form in problems where you might have an initial point and a rate of change.
💡 Note: Conceptual understanding will make problem-solving intuitive and reduce the reliance on mechanical memorization.
Tip 2: Use Visual Aids

The worksheets from Kuta Software often come without accompanying diagrams. Here are some strategies to incorporate visual aids:
- Sketch lines on a grid paper using the given point and slope.
- Use geometric software or online tools to graph lines interactively.
- Discuss or visualize how changing one variable affects the entire line.
| Step | Action |
|---|---|
| 1 | Identify the given point (x₁, y₁) |
| 2 | Draw the point on a coordinate plane |
| 3 | Use slope to draw the line passing through this point |
| 4 | Check your line against the worksheet’s answer |

Tip 3: Practice with Different Scenarios

To solidify your understanding:
- Work through problems with positive slopes, negative slopes, zero slopes, and undefined slopes.
- Try problems where the known point is a y-intercept.
- Apply point-slope form in different contexts like calculating travel distances, plotting stock market trends, or predicting temperature changes.
📝 Note: The more varied your practice, the better equipped you’ll be for real-world applications.
Tip 4: Convert Between Forms
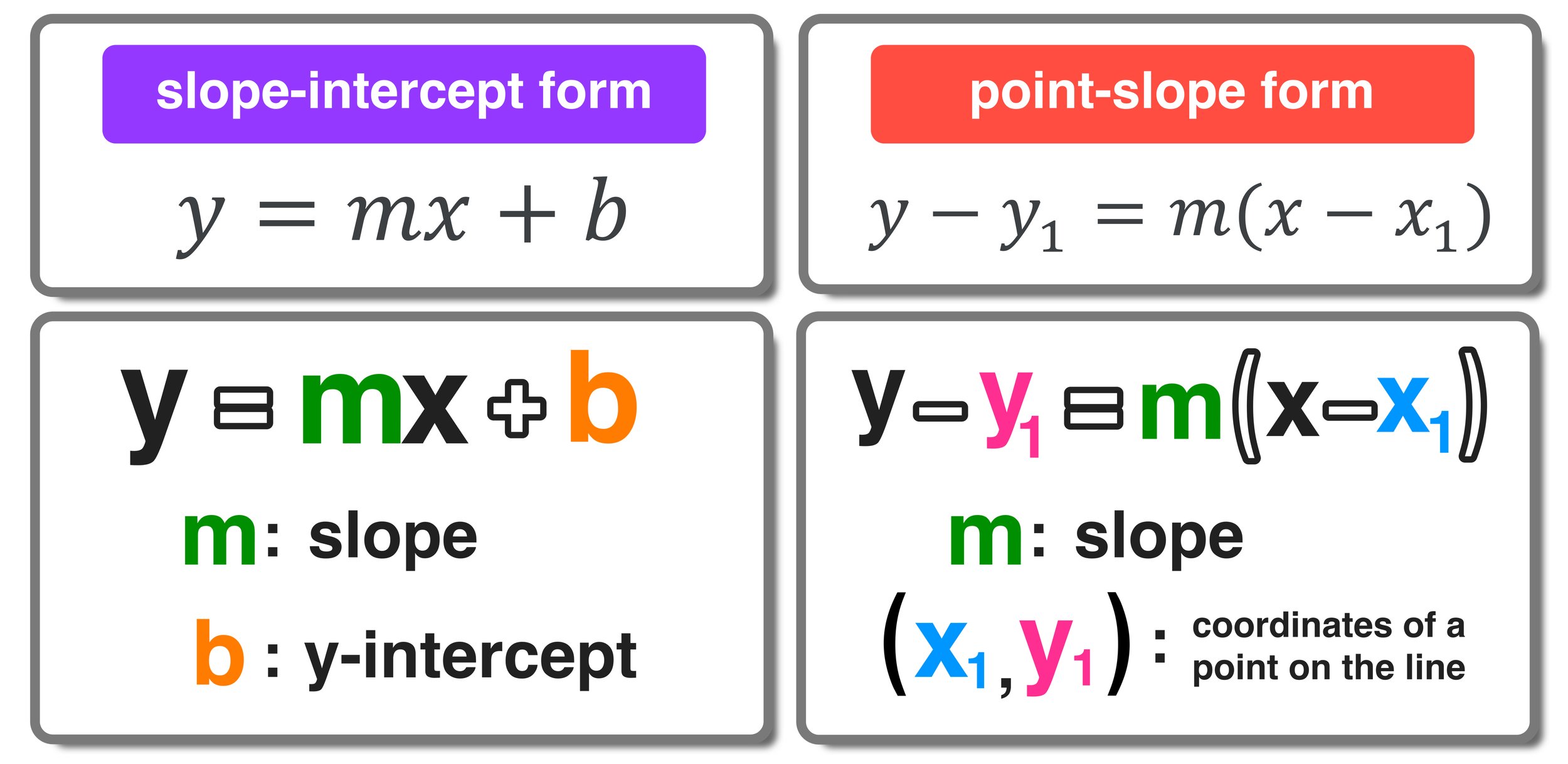
Point-slope form is just one of several ways to write a line’s equation:
- Develop the ability to convert from point-slope to slope-intercept (y = mx + b) and standard form (Ax + By = C).
- This skill is useful for solving equations, graphing, and understanding the different perspectives each form offers.
Tip 5: Engage with Technology

Utilize technology to enhance your learning experience:
- Use graphing calculators or software to instantly plot lines and verify your solutions.
- Explore online simulations or tutorials to see how point-slope form works in dynamic environments.
- Participate in math forums or engage with educational YouTube channels focused on algebra.
Key benefits of using technology include:
- Immediate visual feedback on your work.
- The ability to explore multiple scenarios without manual calculations.
- Access to community insights and different teaching styles.
By following these tips, students and educators can harness the power of point-slope form effectively through Kuta Software worksheets. The journey from understanding the equation to applying it in various contexts becomes clearer, making the process of learning and teaching algebra both fun and fulfilling. Embrace these strategies, and watch as the lines of algebra become not just something to learn but something to appreciate and use in everyday problem-solving.
Why is it important to learn point-slope form?

+
Point-slope form is crucial as it allows you to find the equation of a line when you know a point on the line and the slope. This form is particularly useful in applied problems where initial conditions or rates of change are known.
How can I check my answers for point-slope form?

+
You can verify your answers by graphing the line using the given point and slope. If the line passes through the point with the correct slope, your equation is correct. Additionally, substituting the known point back into your equation should give you a true statement.
Can I use point-slope form in real-world applications?

+
Absolutely! Point-slope form is particularly useful in fields like engineering, physics, and economics. For instance, you can use it to model the trajectory of an object, predict changes in temperature over time, or analyze trends in data.