5 Tips Piecewise Functions

Introduction to Piecewise Functions

Piecewise functions are a type of function that can be defined in different ways for different parts of its domain. This allows for the creation of complex functions that can model real-world phenomena in a more accurate way. In this article, we will explore 5 tips for working with piecewise functions, including how to define them, how to graph them, and how to solve equations involving them.
Tip 1: Defining Piecewise Functions
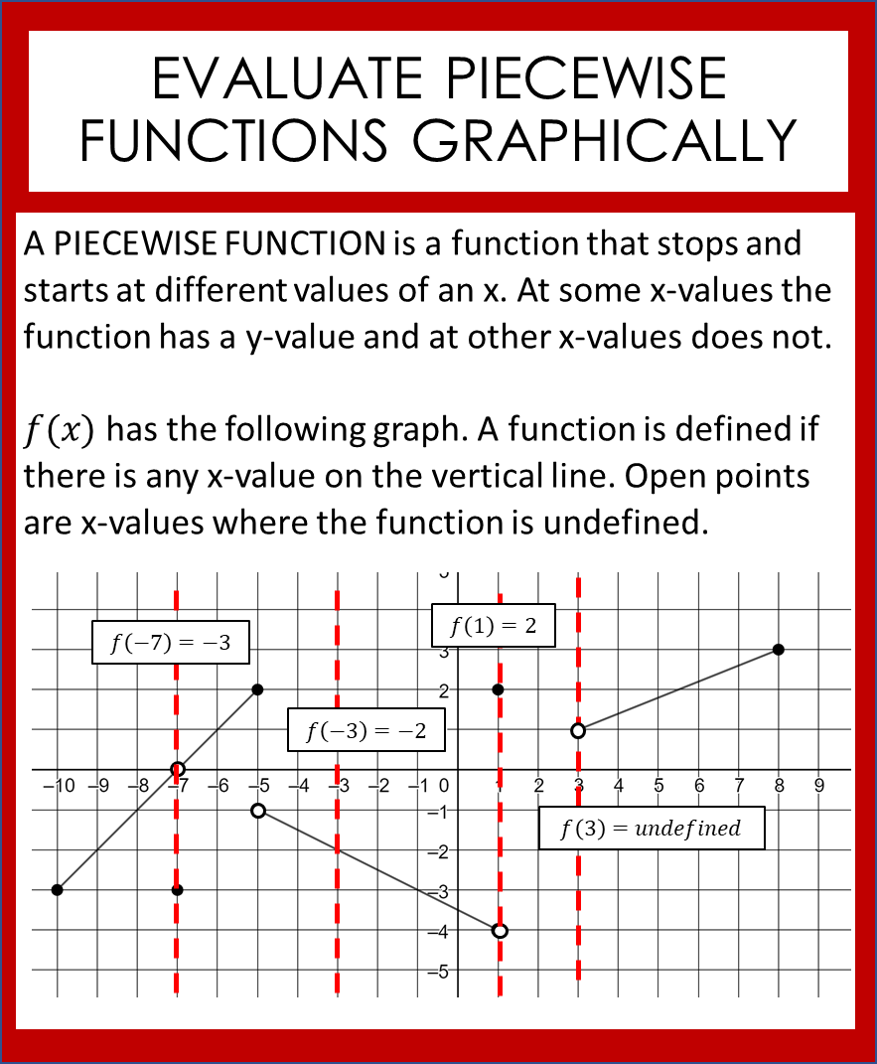
To define a piecewise function, you need to specify the different parts of the domain and the corresponding function definitions. For example, consider the function: [ f(x) = \begin{cases} x^2 & \text{if } x < 0 \ x + 1 & \text{if } x \geq 0 \end{cases} ] This function is defined in two parts: for x < 0, it is equal to x^2, and for x \geq 0, it is equal to x + 1. It is essential to clearly specify the domain for each part of the function to avoid confusion.
Tip 2: Graphing Piecewise Functions
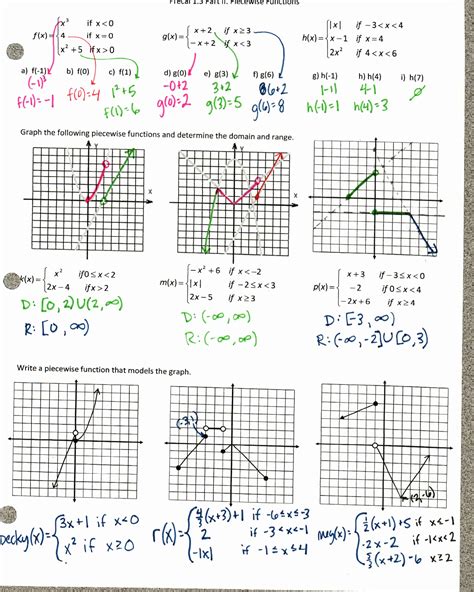
Graphing a piecewise function involves graphing each part of the function separately and then combining the graphs. For the example function above, we would first graph y = x^2 for x < 0 and then graph y = x + 1 for x \geq 0. The resulting graph will show the different parts of the function. It’s crucial to use a dashed line or a different color to indicate the different parts of the domain.
Tip 3: Solving Equations Involving Piecewise Functions

To solve an equation involving a piecewise function, you need to consider each part of the function separately. For example, to solve the equation f(x) = 2, where f(x) is the piecewise function defined above, we would need to solve the equations x^2 = 2 for x < 0 and x + 1 = 2 for x \geq 0. Solving these equations separately will give us the solutions to the original equation.
Tip 4: Working with Piecewise Functions in Calculus
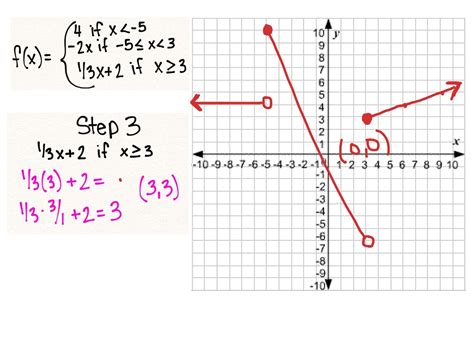
When working with piecewise functions in calculus, we need to consider the different parts of the function separately. For example, to find the derivative of a piecewise function, we would find the derivative of each part of the function separately. It’s essential to check the continuity of the function at the points where the definition changes to ensure that the derivative exists at those points.
Tip 5: Real-World Applications of Piecewise Functions

Piecewise functions have many real-world applications, such as modeling the cost of shipping packages based on weight, the cost of electricity based on usage, and the trajectory of objects under different conditions. For instance, consider a company that charges 5 for shipping packages weighing up to 2 pounds and 10 for packages weighing more than 2 pounds. This can be modeled using a piecewise function: [ C(x) = \begin{cases} 5 & \text{if } x \leq 2 \ 10 & \text{if } x > 2 \end{cases} ] where C(x) is the cost of shipping a package weighing x pounds.
| Weight (pounds) | Cost |
|---|---|
| 0-2 | $5 |
| 2+ | $10 |

📝 Note: When working with piecewise functions, it's essential to consider the different parts of the domain and the corresponding function definitions to avoid errors and ensure accurate results.
To summarize, piecewise functions are a powerful tool for modeling complex real-world phenomena, and understanding how to define, graph, and solve equations involving them is crucial for success in mathematics and related fields. By following these 5 tips, you’ll be well on your way to mastering piecewise functions and applying them to a wide range of problems.
What is a piecewise function?

+
A piecewise function is a function that is defined in different ways for different parts of its domain.
How do I graph a piecewise function?
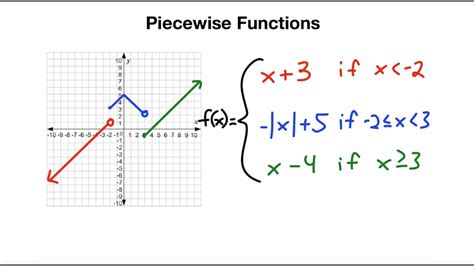
+
To graph a piecewise function, graph each part of the function separately and then combine the graphs.
What are some real-world applications of piecewise functions?

+
Piecewise functions have many real-world applications, including modeling the cost of shipping packages, the cost of electricity, and the trajectory of objects under different conditions.



