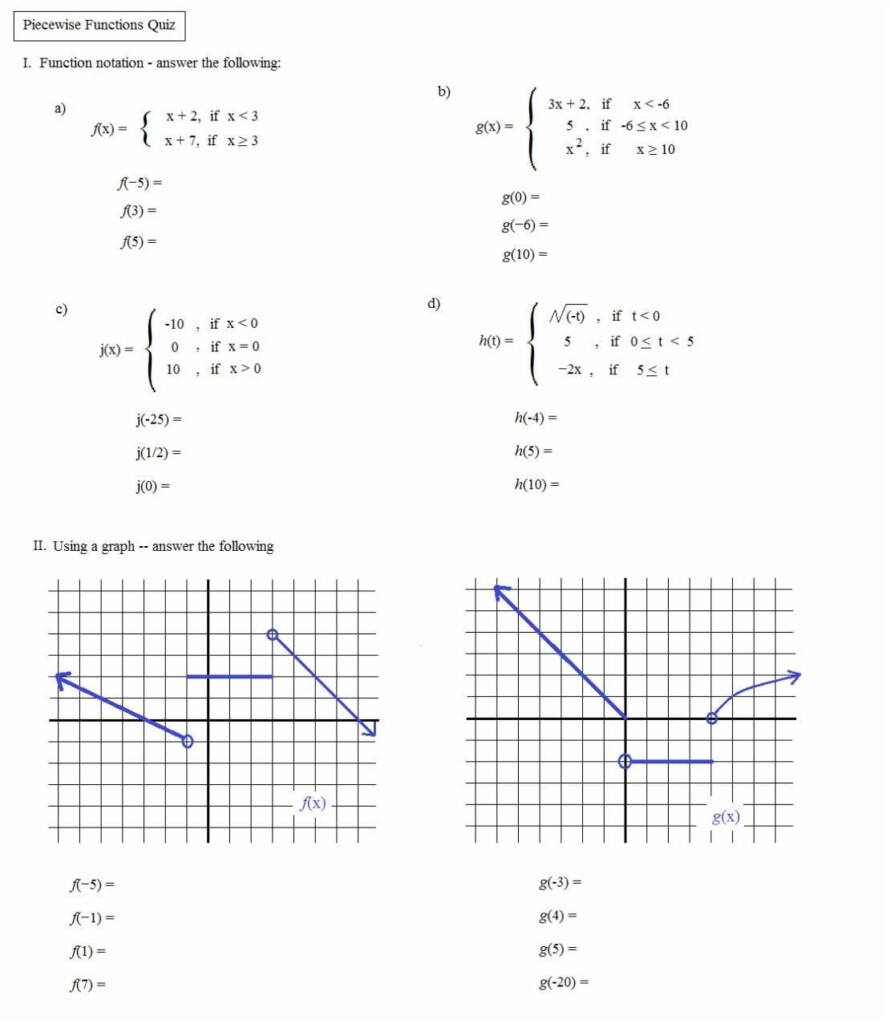
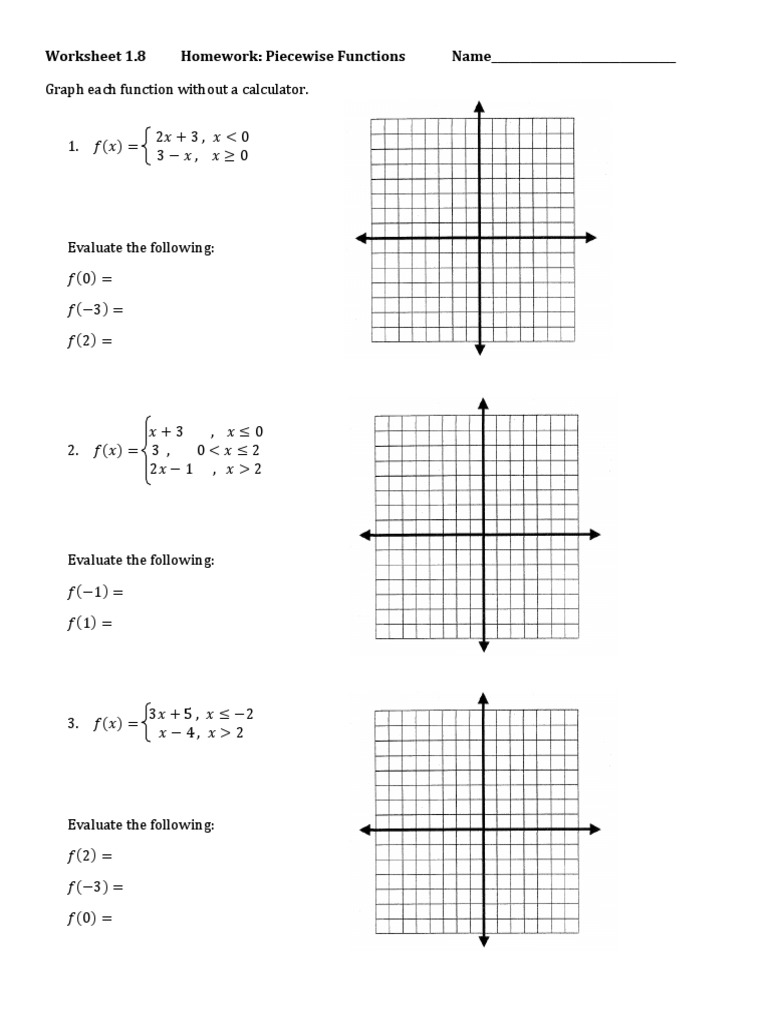
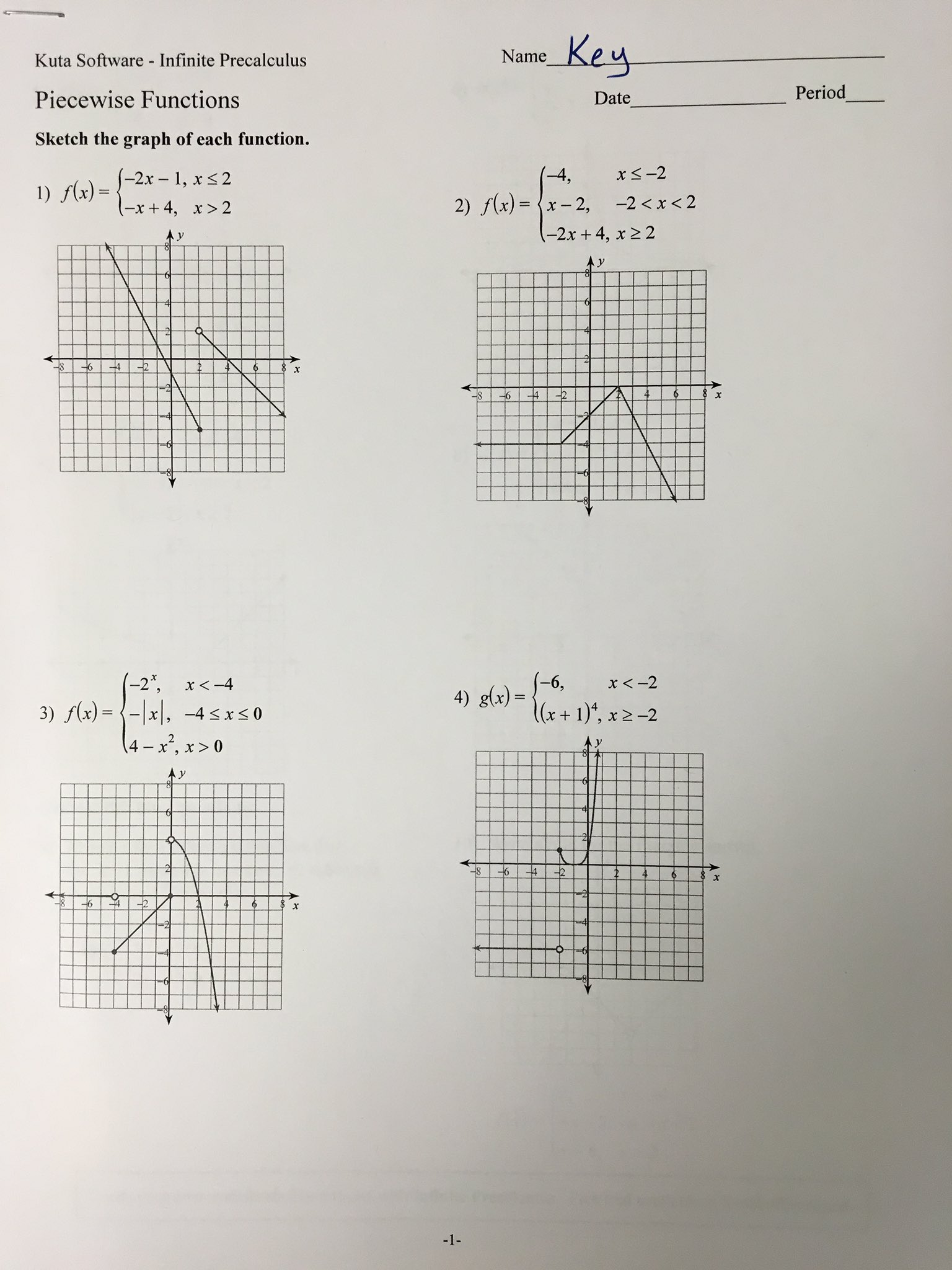
Piecewise Functions Worksheet Answers: Simplify Your Math Study

Understanding piecewise functions can be a challenging part of mathematics, particularly for students at the intermediate and advanced levels. These functions, which are defined by different formulas over various intervals of their domain, require a solid grasp of how to approach and solve them for both practical and theoretical purposes. This comprehensive blog post will not only explain what piecewise functions are but will also guide you through a series of problems, providing solutions to deepen your comprehension.

What are Piecewise Functions?

Piecewise functions are constructed from several pieces of different functions, each corresponding to a specific interval. These intervals collectively cover the entire domain of the function. Understanding these functions is key because:

• They model real-life scenarios where conditions change abruptly or based on certain criteria.
• They help in visualizing functions that are otherwise difficult to express in a single formula.
• They are prevalent in programming, where conditional logic is used to define different outcomes based on input.

Steps to Solve Piecewise Functions

Here’s how to tackle problems involving piecewise functions:

1. Identify the Domain: Determine which interval the input value belongs to.
2. Apply the Correct Function: Once the interval is identified, apply the function formula for that specific interval.
3. Solve the Expression: Work out the function with the given input.

Worksheet Problems and Solutions

Problem 1:

Given the function:

[ f(x) = \begin{cases} x^2 + 3 & \text{if } x < -1 \ -x & \text{if } -1 \leq x < 2 \ x - 1 & \text{if } x \geq 2 \end{cases} ]

Find ( f(-2) ), ( f(0) ), and ( f(3) ).

Solutions:

• To find f(-2) :
  1. -2 < -1 , so we use the function x^2 + 3 .
  2. Calculate: (-2)^2 + 3 = 4 + 3 = 7 .
  3. Therefore, f(-2) = 7 .
• To find f(0) :
  1. -1 \leq 0 < 2 , so we use the function -x .
  2. Calculate: -0 = 0 .
  3. Thus, f(0) = 0 .
• To find f(3) :
  1. x \geq 2 , so we use the function x - 1 .
  2. Calculate: 3 - 1 = 2 .
  3. Hence, f(3) = 2 .

Problem 2:

Evaluate the function:

\[ g(x) = \begin{cases} 2 & \text{if } x < -5 \\ |x| - 2 & \text{if } -5 \leq x < 5 \\ 2 & \text{if } x \geq 5 \end{cases} \]

Find g(-6) , g(-3) , and g(7) .

Solutions:

• To find g(-6) :
  1. -6 < -5 , so we use the function 2 .
  2. Therefore, g(-6) = 2 .
• To find g(-3) :
  1. -5 \leq -3 < 5 , so we use the function |x| - 2 .
  2. Calculate: |-3| - 2 = 3 - 2 = 1 .
  3. Thus, g(-3) = 1 .
• To find g(7) :
  1. x \geq 5 , so we use the function 2 .
  2. Therefore, g(7) = 2 .

Note:

💡 Note: When evaluating piecewise functions, be sure to check the domain boundaries carefully to ensure you use the correct function piece.

Final Thoughts

To summarize, piecewise functions offer an innovative way to address real-world issues by breaking down problems into manageable pieces. They allow for conditional behavior, a trait often seen in computer programming and advanced mathematical modeling. By understanding the intricacies of how these functions work, you can enhance your problem-solving skills, particularly in areas where variables or conditions change abruptly.

These problems, while seemingly complex, illustrate the importance of domain understanding and correct application of formulas. By practicing with more examples, you’ll become adept at interpreting and solving piecewise functions, making them less of a challenge and more of an interesting puzzle to solve.