Perpendicular and Angle Bisectors Worksheet Answers Revealed
Discovering how to use perpendicular and angle bisectors in geometry problems can significantly enhance one's problem-solving skills. Today, we're diving deep into the world of these fundamental geometric tools to not only understand their significance but also to provide detailed answers to common worksheets on the subject. Whether you're a student looking to verify your answers or an educator seeking comprehensive explanations, this post is tailored to demystify these geometric concepts.
Understanding Perpendicular Bisectors

A perpendicular bisector is a line or line segment that divides another line segment into two equal parts at a right angle. Here's what you need to know:
- The midpoint of the segment is where the bisector intersects.
- This line or segment is always perpendicular to the segment being bisected.
- It splits the segment into two equal parts.
Application of Perpendicular Bisectors

In real-life applications, perpendicular bisectors are pivotal in:
- Determining the center of a circle circumscribed around a triangle.
- Finding the points equidistant from the endpoints of a line segment.
- Design and engineering for symmetry, for example, in locating the center of mass or balance in objects.
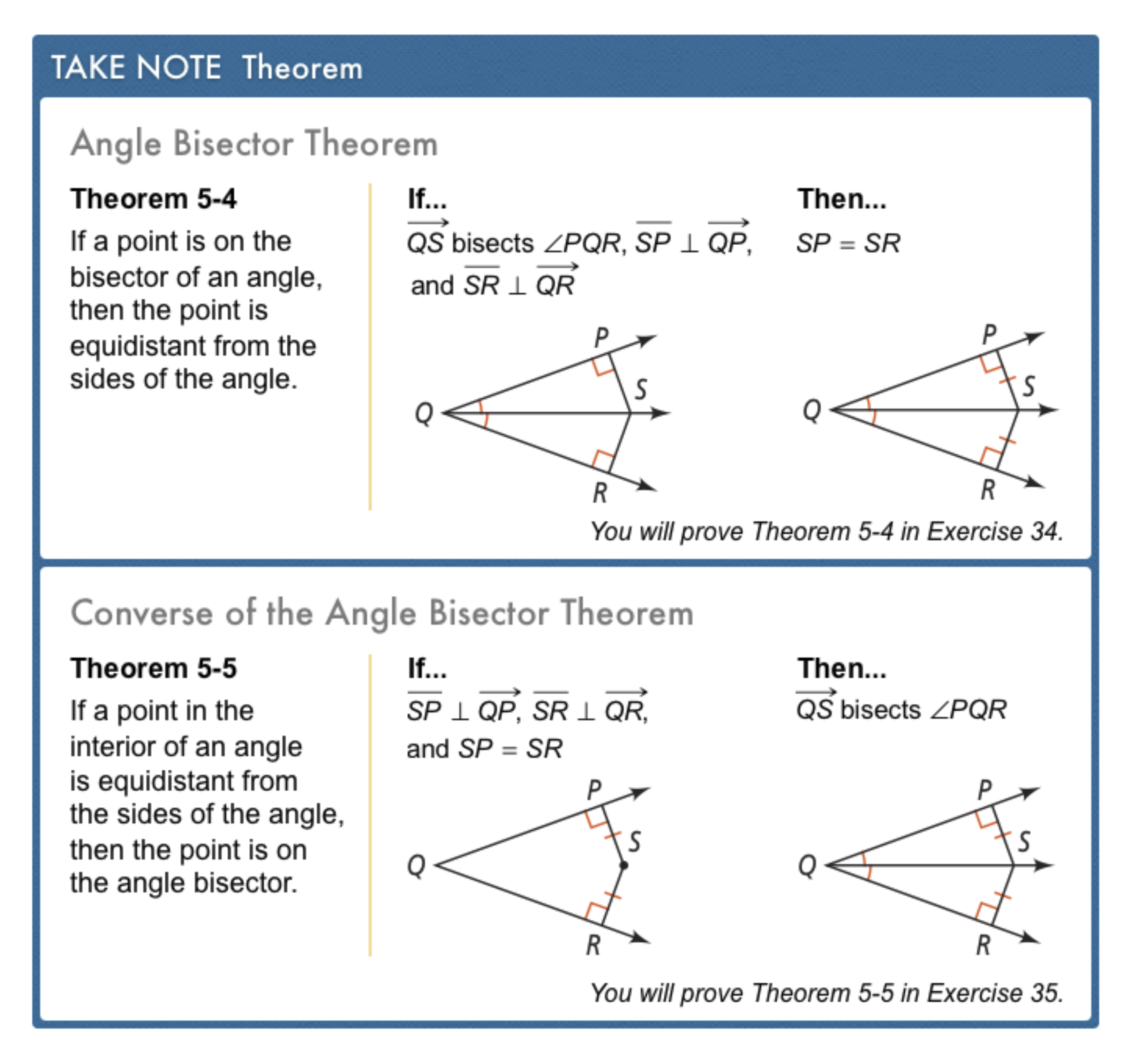
Delving into Angle Bisectors

An angle bisector is a line or line segment that splits an angle into two equal angles. Here's how they function:
- An angle bisector divides the angle equally in half.
- It can be extended through the vertex of the angle or within the angle itself.
- It's used in the triangulation process for navigation, surveying, and architecture.
Uses in Geometry

Here are some key uses of angle bisectors:
- In proving that two sides of a triangle are congruent.
- To find the center of an inscribed circle in a triangle (incenter).
- For constructing polygons where each side or angle needs to be bisected.
Worksheet Answers for Perpendicular Bisectors

To help you navigate through typical perpendicular bisector problems, here are answers to common worksheet exercises:
| Question | Answer |
|---|---|
| 1. Find the perpendicular bisector of segment AB where A(2,3) and B(6,9). | The perpendicular bisector passes through the midpoint of AB, which is (4,6). The line's equation is y = 2x - 2. |
| 2. If D is the midpoint of AB and C is any point not on AB, prove that CD = CB. | Using the definition of perpendicular bisector, since D is the midpoint, the distances from D to C and B must be equal, thus CD = CB. |

📌 Note: When finding the equation of a perpendicular bisector, always remember to use the slope formula, negate it, and find the midpoint.
Worksheet Answers for Angle Bisectors

Now, let's address common angle bisector problems:
| Question | Answer |
|---|---|
| 1. Construct an angle bisector for ∠XYZ where Y is the vertex. | Start by drawing an arc from Y cutting XY and YZ at points P and Q respectively. Then, draw arcs from P and Q with equal radii intersecting at point R. Line YR is the angle bisector. |
| 2. Prove that the angle bisector of an angle divides the opposite side proportionally. | Using the Angle Bisector Theorem, if AD is the angle bisector of ∠BAC in triangle ABC, then AB/AC = BD/DC. |
📌 Note: For constructing angle bisectors, remember to use the same radius for both arcs to ensure accuracy.
Throughout this post, we've explored the concepts and practical applications of perpendicular and angle bisectors, providing detailed explanations and answers to common worksheet questions. These tools are essential in geometry for symmetry, design, and solving various geometric problems. By understanding how to use them correctly, you're equipped to tackle any worksheet or geometric challenge with confidence. In summary, perpendicular and angle bisectors are not just abstract concepts; they have real-world applications that can influence our daily lives in design, engineering, and problem-solving. Whether it's ensuring balance in architectural structures or accurately dividing land plots, the ability to bisect accurately plays a pivotal role. Keep practicing these skills, and you'll find yourself appreciating the beauty and precision of geometry even more.
Why are perpendicular bisectors important in real life?

+
Perpendicular bisectors are crucial for applications like finding the center of a circle or an equilateral triangle, ensuring symmetry in engineering design, and achieving balance in construction and manufacturing processes.
Can you use a perpendicular bisector to divide land plots?

+
Yes, surveyors often use perpendicular bisectors to divide land accurately into equal parts. This ensures that each section of land has equal frontage on a road or water source.
How does the Angle Bisector Theorem apply to triangles?

+
The Angle Bisector Theorem states that an angle bisector of an angle in a triangle divides the opposite side into segments proportional to the adjacent sides. This can be used to solve various problems related to the geometry of triangles.

