Permutations and Combinations Worksheet: Answer Key Revealed

Permutations and Combinations Worksheet: Answer Key Revealed
Welcome to our in-depth look at permutations and combinations, where we simplify the math behind how we count and arrange objects in different ways. Whether you're a student grappling with these concepts for the first time, a teacher looking for resources to explain them, or someone simply curious about how counting can be so complex, this article is tailored to meet your needs. Here, we'll dissect permutations and combinations, explore their applications, and work through a comprehensive worksheet with its answer key revealed.
Understanding Permutations

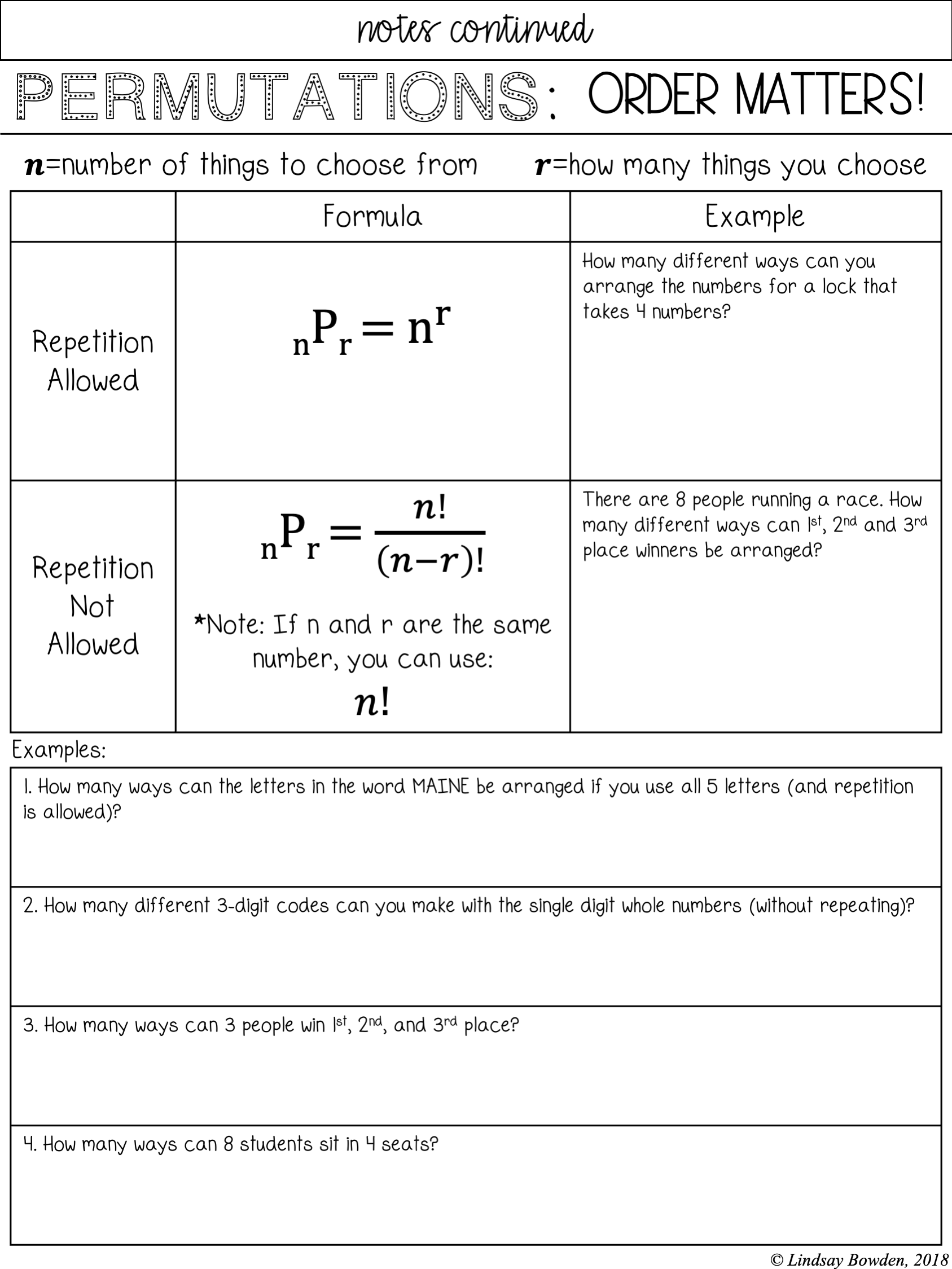
Permutations deal with the arrangement of items where the order matters. Imagine you’re arranging a series of books on a shelf, each different arrangement is a unique permutation. Here’s a basic formula for permutations:
[ P(n, r) = \frac{n!}{(n-r)!} ]
- n - total number of items
- r - number of items being chosen at a time
💡 Note: The factorial, denoted by !, is the product of all positive integers up to that number.
Example Permutations

Let’s say you have three books: A, B, and C. Here are all the possible permutations:
- ABC
- ACB
- BAC
- BCA
- CBA
- CAB
To find how many permutations there are, we use the formula:
[ P(3, 3) = \frac{3!}{(3-3)!} = \frac{6}{1} = 6 ]
Now, let's try a more complex example with given items:
| Scenario | Number of Permutations |
|---|---|
| How many ways to arrange 5 cars in a race? | 120 (5!) |
| How many ways to form a 3-digit number with digits 1-9? | 720 (9P3) |
| How many ways can you rank 6 players in a tennis tournament? | 720 (6!) |

Understanding Combinations

Combinations, on the other hand, are about selecting items where the order does not matter. For instance, choosing a committee from a group of people, where the order in which you select members is irrelevant. Here is the formula for combinations:
[ C(n, r) = \frac{n!}{r!(n-r)!} ]
- n - total number of items
- r - number of items being chosen
💡 Note: When calculating combinations, remember that you are not considering the order, which reduces the total number of outcomes.
Example Combinations

Suppose you are to form a committee of 3 members from a group of 5 friends. The different combinations are:
- A, B, C
- A, B, D
- A, B, E
- A, C, D
- A, C, E
- A, D, E
- B, C, D
- B, C, E
- B, D, E
- C, D, E
Using the combination formula:
[ C(5, 3) = \frac{5!}{3! \cdot 2!} = \frac{120}{6 \cdot 2} = 10 ]
Now, let's look at some other examples:
| Scenario | Number of Combinations |
|---|---|
| How many teams of 4 can be made from 12 players? | 495 (C(12, 4)) |
| How many ways to choose 2 out of 6 desserts? | 15 (C(6, 2)) |
| How many groups of 3 friends can be formed from 8? | 56 (C(8, 3)) |
Worksheet with Answer Key

Below is a sample worksheet that tests your understanding of permutations and combinations, with the answers provided:
Permutations Worksheet

- How many ways are there to arrange the letters in “SIMPLE”?
- In how many ways can 8 people sit around a circular table?
- How many different 4-digit numbers can be made from the digits 1, 2, 3, 4 if no digit can be repeated?
Answer Key

- 720 (6! for SIMPLE)
- 5040 (8! - 1 because circular arrangements have rotational symmetry)
- 24 (P(4, 4))
Combinations Worksheet

- How many different ways can you choose 5 cards from a standard deck of 52?
- How many different 4 member committees can be formed from 10 people?
- From 8 fruits, how many ways can you select a fruit salad of 4 different types of fruits?
Answer Key

- 2,598,960 (C(52, 5))
- 210 (C(10, 4))
- 70 (C(8, 4))
📝 Note: Always double-check calculations by reducing factorials where possible, to avoid unnecessary multiplication.
We've now gone through the essential principles of permutations and combinations, from basic definitions to real-world applications. Understanding these concepts can be a gateway to not only excelling in mathematics but also in fields like statistics, computer science, and even everyday problem-solving scenarios.
What’s the difference between permutations and combinations?
+
Permutations consider the order of arrangement, whereas combinations do not. For example, in permutations, ABC is different from ACB; in combinations, these are considered the same.
How can I easily remember when to use permutations or combinations?

+
If the order in which items are chosen matters, use permutations. If it doesn’t, use combinations.
Are there any practical examples of permutations and combinations?

+
Yes! Permutations are used in scheduling, passwords, and lottery numbers where order matters. Combinations are used in creating teams, forming committees, or selecting items where order doesn’t matter.
How does one handle permutations with identical objects?

+
If you have multiple identical items, you divide by the factorial of the count of each identical item. For example, in permuting the letters in MISSISSIPPI, you’d use:
[ \frac{11!}{1! \cdot 4! \cdot 4! \cdot 2!} ]What are some strategies for simplifying large combination calculations?
+You can often cancel out factors in the numerator and denominator. Also, using the property that C(n, r) = C(n, n-r) can reduce the magnitude of calculations for larger n and r.