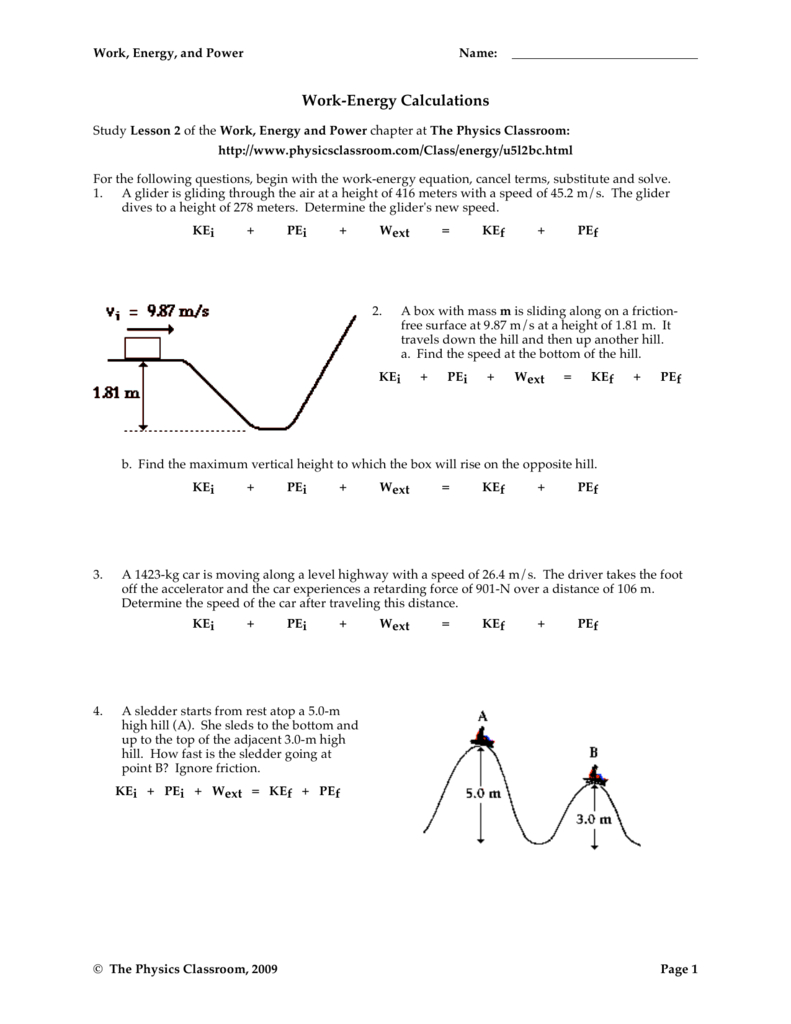
5 Perimeter Word Problems for Math Mastery

The mastery of mathematical concepts isn't just about understanding formulas but also about applying these formulas to real-world scenarios. Perimeter word problems serve as an excellent bridge between theoretical understanding and practical application. Here, we delve into five unique perimeter word problems that will not only test your understanding of geometry but also sharpen your problem-solving skills. Let's explore how perimeter can manifest in daily life and how mastering this concept can be not only educational but also fun!
The Basics of Perimeter

Before tackling word problems, it's crucial to understand what perimeter is:
- The perimeter is the total length of the boundary of a shape.
- For common shapes like squares, rectangles, and triangles, we have straightforward formulas:
- Square Perimeter:
P = 4 * Side - Rectangle Perimeter:
P = 2 * (Length + Width) - Triangle Perimeter:
P = Side1 + Side2 + Side3
- Square Perimeter:
- Real-world examples include fencing a yard, framing a painting, or laying out a running track.
Problem 1: The Garden Bed Dilemma

Imagine you have a garden bed shaped like a rectangle with dimensions of 12 feet by 8 feet. You want to add a border of stones around the garden. How many feet of stones do you need?
- Calculate the perimeter:
P = 2 * (12 + 8) = 2 * 20 = 40feet.
💡 Note: If considering both the inner and outer perimeter for a border, remember to account for the width of the border material.
Problem 2: The Schoolyard Mystery

Your school is considering painting its perimeter to make the space more visually appealing. The schoolyard is a square with an area of 2500 square meters. What will be the length of paint required?
- Find the side length:
Side = sqrt(Area) = sqrt(2500) = 50meters - Then, calculate the perimeter:
P = 4 * 50 = 200meters.
Problem 3: Triangular Lawn Mowing

You're tasked with mowing a triangular plot of land. The sides of the triangle measure 6, 8, and 10 meters. How long does your mower need to cover all sides?
- Sum up the sides for the perimeter:
P = 6 + 8 + 10 = 24meters.
Problem 4: The Haunted House Enclosure

A local amusement park wants to fence in a spooky house exhibit, which has an unusual shape. They need fencing around a semicircle (the back half of the house) with a straight-line front. If the straight-line segment is 30 feet and the diameter of the semicircle is 60 feet, how much fencing is needed?
- The front fence is already given: 30 feet.
- The arc length of the semicircle:
(π * Diameter) / 2 = (3.14 * 60) / 2 ≈ 94.2feet. - Total fencing:
30 + 94.2 = 124.2feet.
Problem 5: The Road Runner's Escape

A cartoon roadrunner needs to avoid a coyote trap by running around a rectangular trap. The trap is 20 meters by 15 meters, and he must run around it three times. What is the total distance he will cover?
- Calculate the perimeter once:
P = 2 * (20 + 15) = 70meters. - Multiply by the number of laps:
70 * 3 = 210meters.
Working through these perimeter word problems offers not only a deep dive into the practical applications of mathematics but also illustrates the beauty and utility of geometry in everyday life. Whether you're designing a garden, managing a property, or simply looking to understand your surroundings better, perimeter calculations provide insights into spatial relationships that are fundamental to our interaction with the world.
Why is it important to understand perimeter in real-life applications?

+
Perimeter understanding is vital for tasks like determining fencing needs, landscaping, and understanding space and layout in property management.
Can perimeter problems involve shapes other than rectangles and squares?

+
Yes, perimeter calculations can involve any polygon or even curved shapes like circles or semicircles, where you’d consider the arc length as part of the perimeter.
How can I use perimeter to estimate material needed for a project?
+
By calculating the perimeter of the area you’re working on, you can determine the linear footage needed for materials like fencing, trim, or border stones.