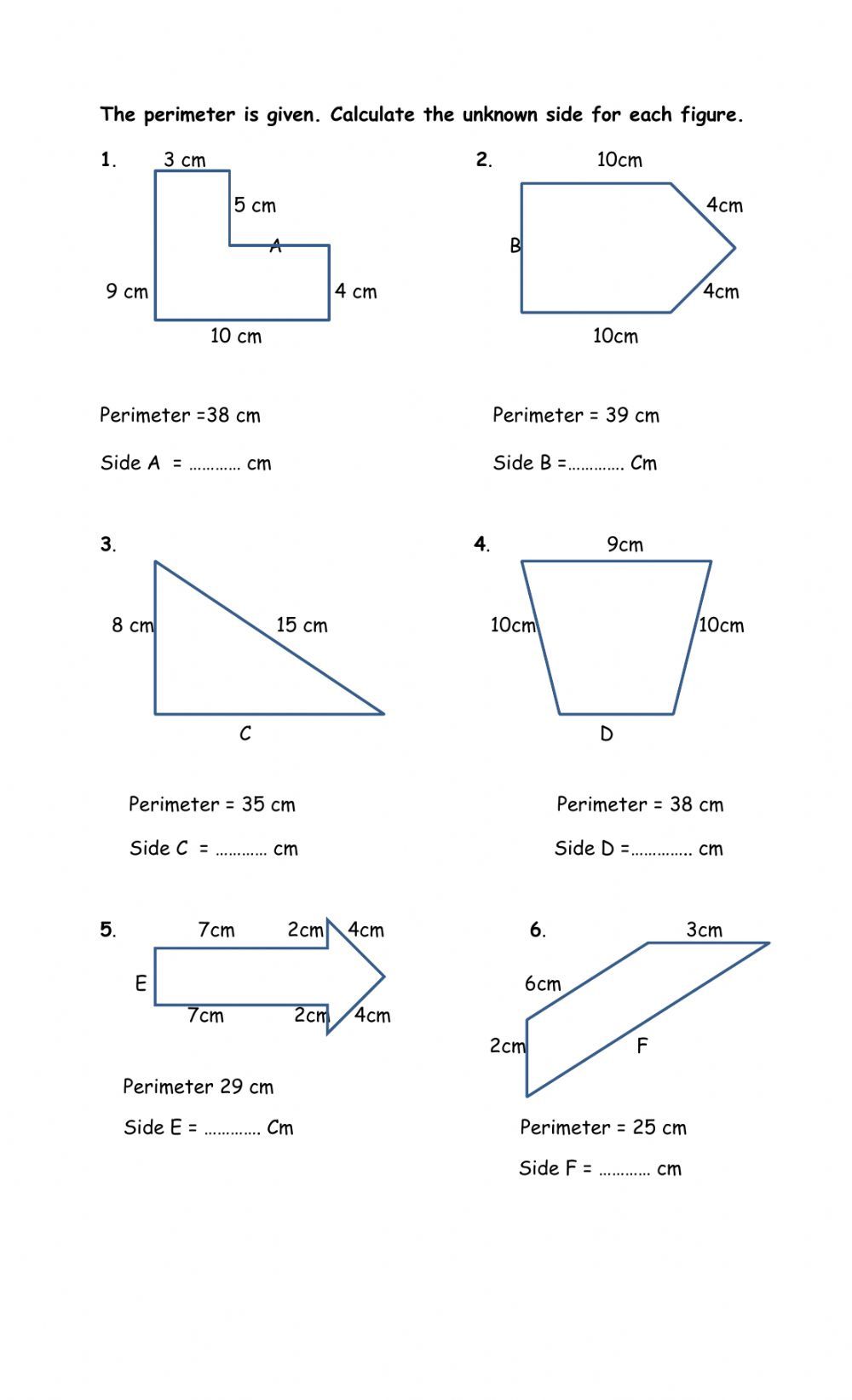
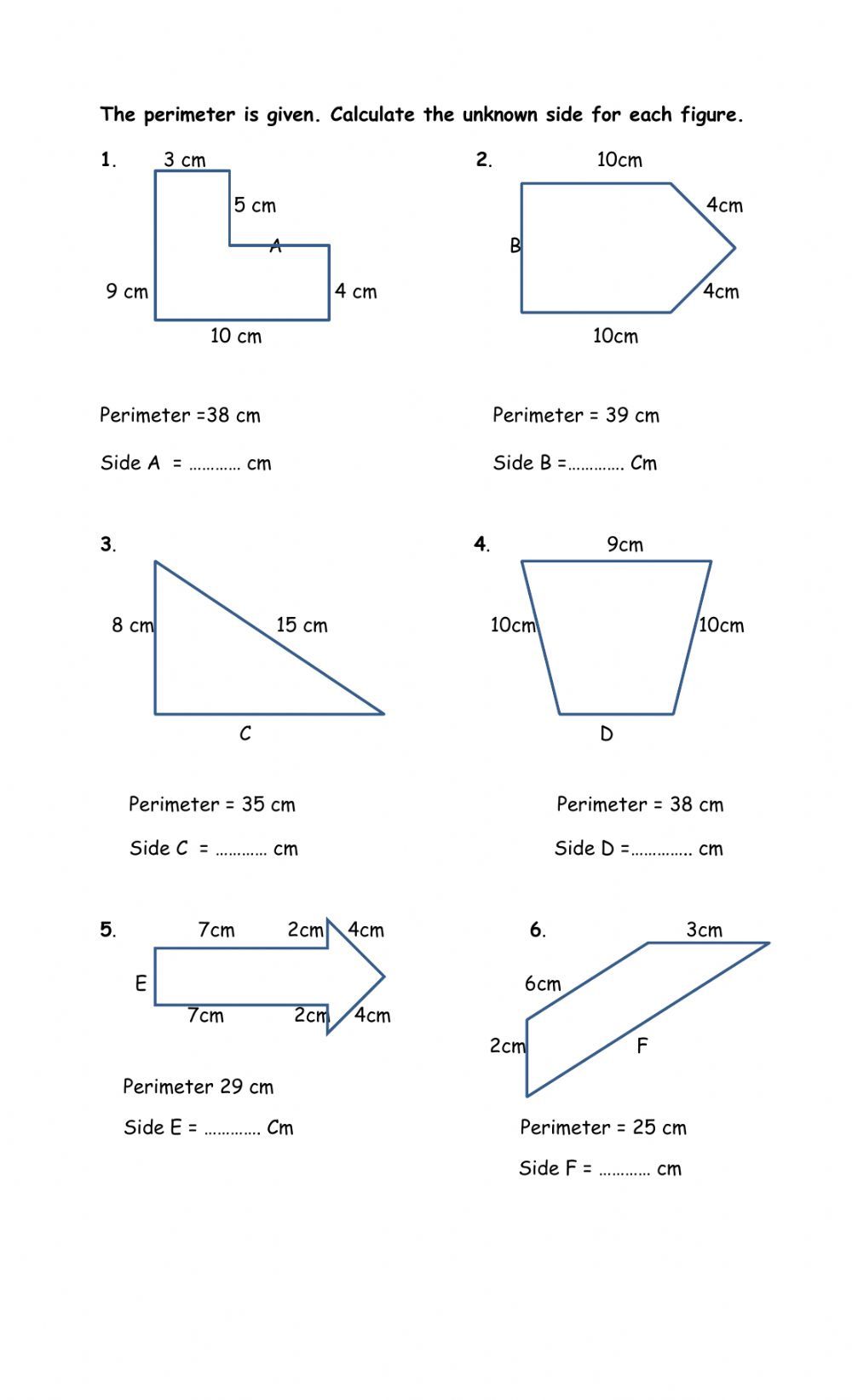
5 Tips for Solving Perimeter Missing Side Worksheets

When students encounter geometry problems, particularly those involving finding a missing side in perimeter calculations, they can often feel overwhelmed. However, with the right strategies, solving perimeter missing side worksheets can become straightforward and even fun. Here are five tips to help you master these problems:
Understand the Basics of Perimeter


Before diving into complex problems, ensure you have a solid grasp on what perimeter means. The perimeter of a shape is the total length of all its sides. For example:
- Square: All sides are equal, so if one side is s, then the perimeter is 4s.
- Rectangle: If you know the lengths of both adjacent sides, say l and w, then the perimeter is calculated as 2l + 2w.
- Triangle: Simply sum all three sides, a + b + c.
📚 Note: When you know most of the sides, you can still find the missing one using basic algebra principles.
Employ the Pythagorean Theorem

Often, when you’re dealing with shapes like right triangles, the Pythagorean theorem can come in handy. If you’re missing one of the triangle’s sides, use:
a² + b² = c², where c is the hypotenuse.
Here’s how it works:
- Identify which sides you know and which one you need to find.
- Substitute the known values into the theorem.
- Solve for the unknown side by rearranging and calculating.
Example: Given a right triangle with sides 5 cm and 12 cm, to find the hypotenuse:
5² + 12² = c²
25 + 144 = c²
169 = c²
c = √169
c = 13 cm
Create a Formula-Based Approach

Each shape has its own perimeter formula. Creating a mental map or writing down these formulas can speed up your problem-solving:
| Shape | Formula |
|---|---|
| Square | P = 4s |
| Rectangle | P = 2(l + w) |
| Triangle | P = a + b + c |

When dealing with more complex shapes or polygons, you might need to combine formulas or even create a custom formula by adding all known sides.
Use Visual Aids and Sketching


Visualizing the problem can often simplify the solution process. Here are some strategies:
- Sketch: Draw the shape, marking known sides with their lengths.
- Label: Clearly label sides to keep track of what's given and what needs to be found.
- Estimate: Sometimes, a quick visual estimate can give you a ballpark figure, reducing the computational load.
🎨 Note: Sketching not only helps with understanding the problem but also with identifying any symmetry or pattern in the shapes, which can streamline calculations.
Work Backwards

If you’re stuck, try working backwards from the given perimeter:
- Understand the total perimeter.
- Calculate the known sides’ sum.
- Subtract this sum from the perimeter to find the missing side.
For instance, if you know the perimeter of a triangle is 15 cm, and two sides are 5 cm each, the missing side would be:
15 cm - (5 cm + 5 cm) = 5 cm
🔄 Note: This approach is particularly effective for simple polygons where you only have one missing side.
By employing these five strategies, your ability to solve perimeter missing side worksheets will see significant improvement. Geometry is all about logical thinking, and with practice, these problems become exercises in quick mental arithmetic and problem-solving.
In essence, mastering these techniques ensures you can approach any geometry problem with confidence. Whether it's understanding the basic principles, leveraging algebraic formulas, utilizing visual aids, or thinking backwards from known values, each strategy builds on the other to form a solid foundation for tackling missing side problems.
Why is it important to know the perimeter in geometry?

+
Perimeter helps in understanding and measuring the boundary of an object or shape. It’s crucial in real-world applications like fencing, fabric measuring, and more, ensuring you have the right amount of material.
Can these tips be applied to all geometric shapes?
+
Yes, while the formulas may differ, the principles like understanding basic concepts, using algebra, visualization, and reverse calculation can be adapted to any geometric shape.
How do you handle shapes with complex perimeters?
+
For complex shapes, you might need to break them down into simpler components, apply the tips separately, or use calculus for shapes with curved boundaries like circles.