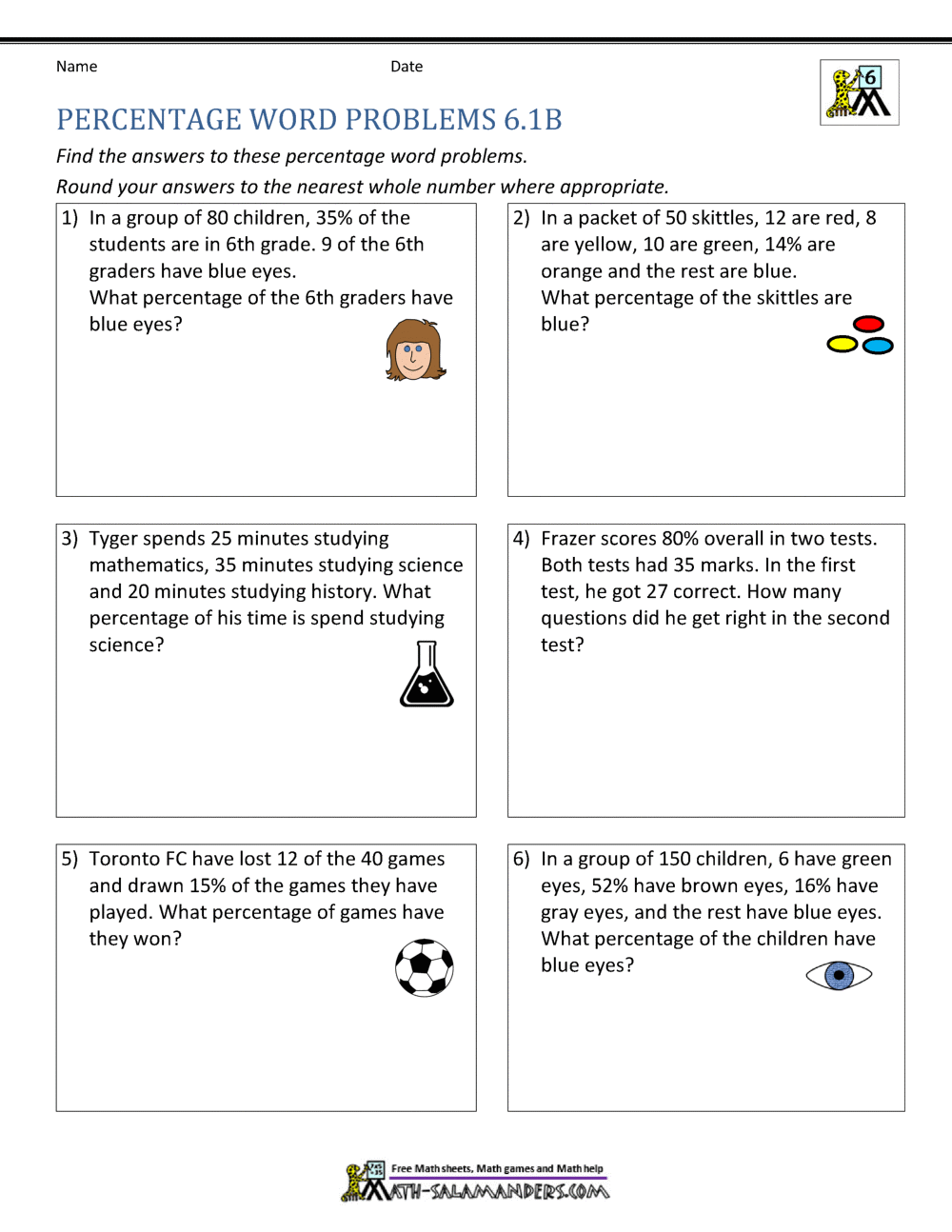
5 Must-Know Strategies for Percent Word Problems

Mastering the Art of Solving Percent Word Problems

Percent word problems often stir a wave of confusion, yet with the right strategies, they become surprisingly simple. Whether you're solving for percentage increases, decreases, or finding an original amount, there are effective techniques you can employ to navigate these mathematical dilemmas smoothly. Here, we delve into five crucial strategies that will transform your approach to percent word problems, ensuring you not only solve them correctly but also understand the underlying principles.

Strategy 1: Grasp the Basics of Percentage

Before diving into complex problems, make sure you understand what a percentage is:

• Percent means 'per hundred'. Thus, 50% equates to 50 per 100 or 0.50.
• Conversions are your allies:
  • To change a percent to a decimal, move the decimal point two places to the left (e.g., 40% = 0.40).
  • Conversely, to convert a decimal to a percent, move the decimal point two places to the right (e.g., 0.65 = 65%).

💡 Note: A solid grasp of these fundamental conversions will save you from errors in more complex percent problems.

Strategy 2: Use the Percent Equation

The formula P * W = V, where:

• P is the percent, expressed as a decimal,
• W is the "whole" or total amount,
• V is the "value" or part you are calculating.

Here's how to apply it:

• Find a Percentage of a Number: P * W = V. If you need to find 30% of 200, calculate 0.30 * 200 = 60.
• Determine the Original Amount: Rearrange to V / P = W. If 45 is 15% of a number, 45 / 0.15 = 300.
• Find the Percent Increase or Decrease: Use the formula:
  • For increase: ((V - W) / W) * 100.
  • For decrease: ((W - V) / W) * 100.

🔧 Note: The percent equation is versatile and covers most percent word problems you encounter.

Strategy 3: Set Up Equations

When faced with a word problem, translate the problem into an equation:

1. Identify: What are you solving for?
2. Variables: Let x be the unknown variable.
3. Set Up: Write an equation based on the problem's information.

For example:

Example: "A shirt was originally priced at $50. It is now on sale for 40% off. What is the new price?"

• The original price is the "whole": W = 50.
• The percentage off (40%) is the percent: P = 0.40.
• The discount (V) is what we're solving for: 0.40 * 50 = V. V = 20 (the discount).
• Subtract the discount from the original price to find the new price: $50 - $20 = $30.

Strategy 4: Apply Proportions

When dealing with situations where items or quantities are proportional to percentages, set up and solve proportions:

Example: "A batch of cookies needs 3 cups of flour to make 60 cookies. If you want to make 120 cookies, how much flour will you need?"

• The proportion is 3 cups of flour / 60 cookies = X cups of flour / 120 cookies.
• Solve for X: 3 / 60 = X / 120, thus X = (3 * 120) / 60 = 6 cups of flour.

📏 Note: Proportions simplify problems where direct relationships between quantities are involved.

Strategy 5: Practice Dimensional Analysis

Use this method to convert units or solve for percentages when different units are involved:

Example: "You need to dilute a 25% pesticide solution to 10% by mixing it with water. How much water should you add to 200 liters of the original solution?"

• Setup the equation for the diluted solution:
• Volume of pesticide in new solution: 0.25 * 200 = 50 L.
• Let X be the volume of water added. The total volume will be 200 + X, and the concentration of pesticide in the new solution will be 50 / (200 + X) = 0.10.
• Solve for X: 200 + X = 50 / 0.10, thus X = 500 - 200 = 300 liters of water.

💦 Note: Dimensional analysis helps keep track of units, ensuring accurate conversions and solutions.

Mastering percent word problems is not about just memorizing formulas but understanding how to apply these strategies. Here's the takeaway:

• Understand the basics of percentage conversions.
• Use the percent equation for a variety of problems.
• Translate problems into solvable equations.
• Apply proportions when items or quantities are related.
• Employ dimensional analysis for unit conversions and complex problems.

This holistic approach not only equips you to solve these problems more efficiently but also enriches your mathematical thinking, making you adept at tackling any percent-related challenge that comes your way.

What are the common mistakes to avoid when solving percent word problems?

+

Common mistakes include forgetting to convert percentages to decimals or fractions, misinterpreting the problem (e.g., calculating a percentage of a number instead of the percentage increase), and not keeping track of units when doing conversions.

How do I find the percent change in word problems?

+

Calculate percent change by subtracting the initial value from the final value, divide by the initial value, then multiply by 100 to express the result as a percentage. The formula is: ((V - W) / W) * 100% where V is the final value, and W is the initial value.

Can I use these strategies for more advanced percent problems?

+

Yes, these strategies provide a foundation for understanding and solving advanced percent problems. The principles remain the same, but you might need to use algebraic manipulation or more complex setups to solve for multiple variables or conditions.