Pascal's Triangle Worksheet: Master the Math Fun Easily

Understanding Pascal's Triangle isn't just about math; it's about discovering the beauty of patterns in numbers. This blog post is dedicated to making your journey through Pascal's Triangle engaging and easy. Whether you're a student preparing for an exam or a curious mind wanting to explore mathematical wonders, this worksheet will guide you through the intricacies of Pascal's Triangle with practical examples, exercises, and insightful explanations.
The Basics of Pascal’s Triangle

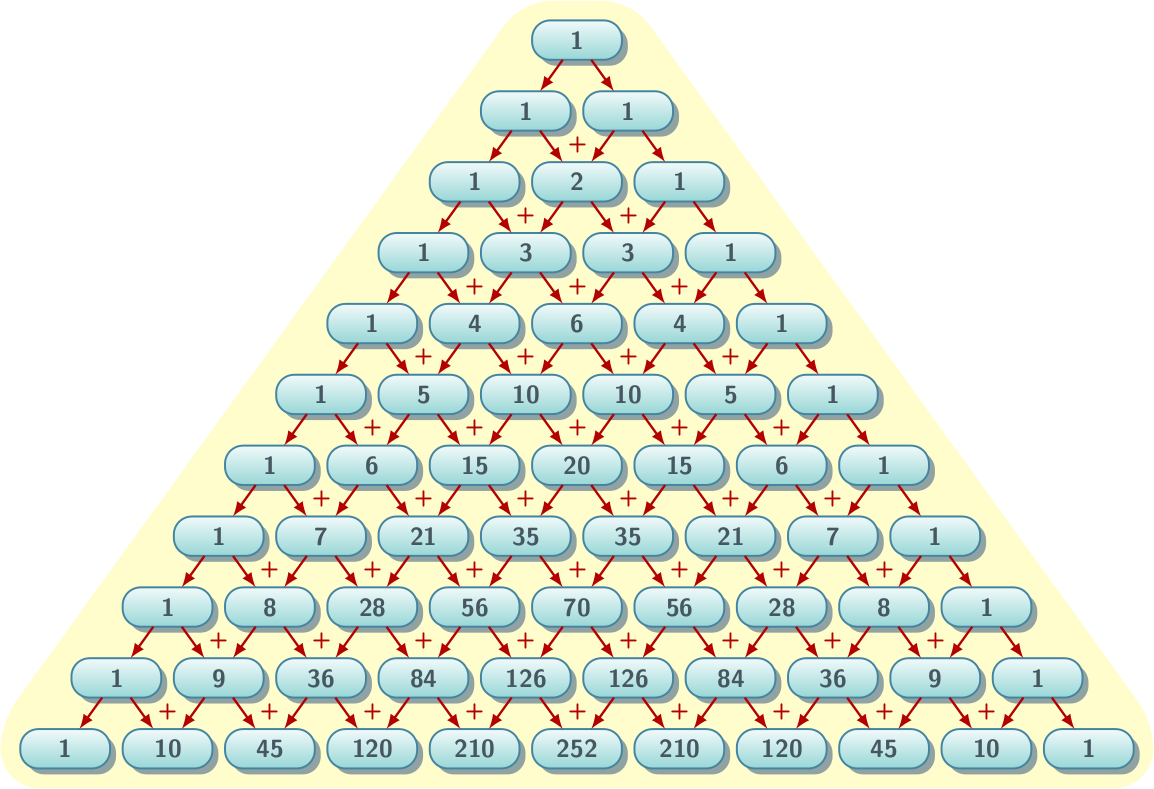
Pascal’s Triangle is a triangular array of numbers that starts with 1 at the top and each subsequent row is constructed by adding adjacent numbers from the row above. Let’s delve into how it’s constructed:
- Top Row: Always begins with a single 1.
- Subsequent Rows: Each entry is the sum of the two numbers directly above it. For example:
| Row | Elements |
|---|---|
| 0 | 1 |
| 1 | 1, 1 |
| 2 | 1, 2, 1 |
| 3 | 1, 3, 3, 1 |

Example Construction

Let’s construct the fourth row:
- Start with 1.
- Add the first two numbers from the row above (1 + 3 = 4).
- Add the second and third numbers (3 + 3 = 6).
- Add the third and fourth numbers (3 + 1 = 4).
- End with 1.
This gives us the row: 1, 4, 6, 4, 1.
💡 Note: In Pascal's Triangle, the sum of the numbers in each row is a power of 2. This can be a useful property for quick checks.
Key Patterns and Properties of Pascal’s Triangle

Beyond its simple construction, Pascal’s Triangle is rich with mathematical properties and patterns:
- Binomial Coefficients: The entries in Pascal’s Triangle represent the binomial coefficients. For example, (1, 3, 3, 1) in row 3 are the coefficients for the expansion of (a + b)3.
- Symmetry: Each row is symmetric. The numbers on the left side mirror those on the right.
- Hockey Stick Pattern: If you sum up the numbers along a diagonal that ends at a chosen number, the sum will be the number directly below the end of that diagonal.
To illustrate, here's a visual representation:

Exercises

Practice these exercises to solidify your understanding:
- Expand (x + y)4 using Pascal's Triangle.
- Find the sum of all elements in the 7th row of Pascal's Triangle.
Applications of Pascal's Triangle

Pascal's Triangle isn't just for academic exploration; it has practical applications:
- Probability: It's used to determine the likelihood of events in probability theory.
- Combinatorics: Helps in solving problems related to combinations and permutations.
- Computing: Useful in algorithms and data compression techniques.
- Start with a blank piece of paper or a spreadsheet.
- Sketch the initial triangle and number the rows for reference.
- Add exercises for:
- Identifying and writing down rows up to a certain number.
- Finding sums and patterns within the triangle.
- Using the triangle for binomial expansion.
- Include space for notes on patterns and insights.
✅ Note: Pascal's Triangle also appears in fractal geometry, specifically Sierpinski's Triangle, which you can explore for a deeper connection between math and art.
Building Your Own Pascal’s Triangle Worksheet
Here’s how you can create your own Pascal’s Triangle worksheet for better learning:
Here's a simple exercise template:
| Row | Elements |
|---|---|
| 4 | _____ |
| 5 | _____ |
| 6 | _____ |
📝 Note: Creating your worksheet can also be a collaborative effort, which is excellent for reinforcing your understanding through teaching others.
In summary, understanding Pascal's Triangle opens doors to countless applications in mathematics and beyond. It's not just a theoretical construct; it's a tool for problem-solving, pattern recognition, and even real-world applications in fields like computer science. By diving deep into Pascal's Triangle, you're not only mastering a mathematical structure but also enhancing your analytical skills and your appreciation for the inherent patterns in the world of numbers.
How do I find specific rows in Pascal’s Triangle quickly?

+
You can calculate each element using the binomial coefficient formula or refer to a pre-computed table for larger rows.
Can Pascal’s Triangle help in understanding Fibonacci numbers?

+
Yes, by summing the diagonals of Pascal’s Triangle, you obtain the Fibonacci sequence.
What is the significance of the Hockey Stick Pattern in Pascal’s Triangle?

+
This pattern highlights how sums of elements along a diagonal are equal to a specific element directly below, demonstrating the mathematical beauty of Pascal’s Triangle.



