5 Essential Parts of an Expression Worksheet Explained

If you're a student or teacher of mathematics or linguistics, you've likely come across the term "expression" numerous times. Expressions, whether algebraic or mathematical, serve as the building blocks for complex calculations and language processing. An expression worksheet can be a potent tool for understanding, practicing, and mastering this fundamental concept. Here, we explain five essential parts of such worksheets that are critical for comprehensive learning.
The Structure of Expressions


The first part of an expression worksheet often focuses on understanding the structure of expressions. Whether you're looking at polynomials, algebraic expressions, or linguistic constructs, recognizing their components is crucial:
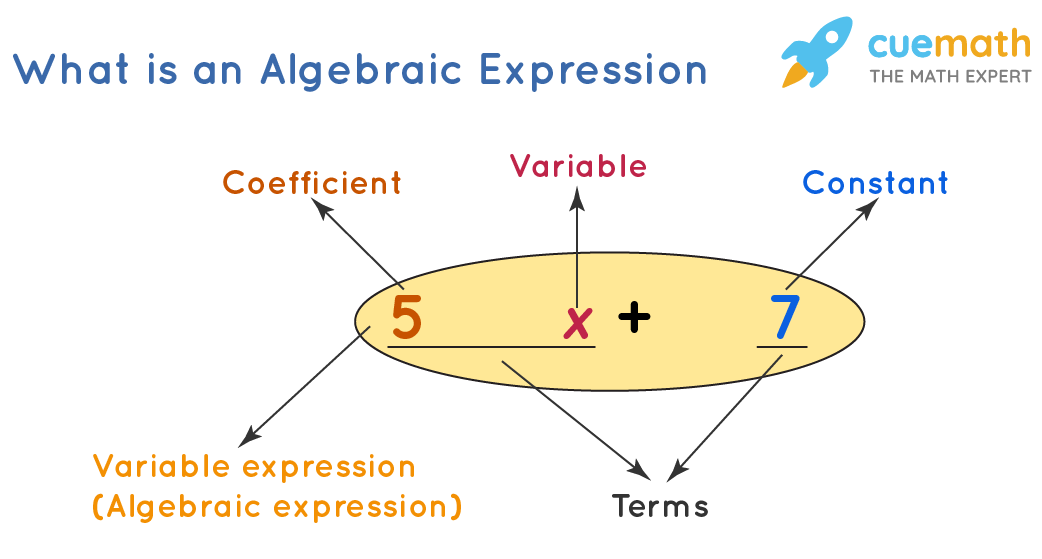
- Variables: Placeholders for values that vary or are unknown.
- Constants: Fixed values within expressions.
- Operations: Signs that indicate operations like addition, subtraction, multiplication, and division.
- Grouping Symbols: Parentheses, brackets, or braces to indicate order of operations.
📝 Note: The structure of expressions sets the foundation for the rest of the learning in math and linguistics. It's imperative to fully grasp this concept as it informs all subsequent parts.
Types of Expressions


After understanding the structure, identifying and differentiating various types of expressions is the next essential step. Here are the most common:
- Algebraic Expressions: Involve constants, variables, and mathematical operations, like
5x + 3. - Arithmetic Expressions: Involve operations on numbers like
15 + 2. - Logical Expressions: Statements that evaluate to true or false, like
a AND b. - Regular Expressions: Patterns used to match strings in text processing.
💡 Note: Understanding the types of expressions is like knowing the different genres of literature. Each serves a unique purpose in the mathematical or linguistic context.
Evaluation and Simplification


One of the most practical parts of an expression worksheet is teaching the skills of evaluation and simplification:
- Evaluation: Substituting variable values into expressions to find their numeric value.
- Simplification: Reducing expressions to their simplest form by combining like terms, removing unnecessary parentheses, etc.
🛑 Note: Always remember that expressions must be evaluated in the context of their intended domain, and simplification doesn't always mean smaller numbers; it means a more straightforward expression.
Translating Between Expressions and Words


Expressions often represent real-world problems. Thus, the ability to translate between expressions and their verbal or written equivalents is invaluable:
- From words to expressions: Phrasing mathematical problems in expression form.
- From expressions to words: Writing out what an expression means in plain language.
📝 Note: This part of the worksheet can bridge the gap between abstract mathematical concepts and their real-world applications.
Problem Solving with Expressions


The final piece of the puzzle is applying what you've learned to solve real-world or theoretical problems. This could involve:
- Modeling: Creating mathematical or linguistic models using expressions.
- Solving: Using expressions to solve for unknowns, applying algebraic rules.
🔍 Note: Problem-solving requires not just knowing expressions but also understanding how to manipulate and combine them to achieve desired outcomes.
In summary, expression worksheets are more than just writing out variables and numbers. They're a crucial learning tool that provides a systematic approach to understanding and using expressions in various contexts. These five essential parts - understanding structure, identifying types, evaluation and simplification, translation, and problem solving - encapsulate the core aspects of working with expressions, whether you're solving equations or interpreting text patterns. Mastering these parts equips students with the skills to tackle both mathematical and linguistic challenges effectively.
What’s the difference between a variable and a constant?

+
A variable represents an unknown or changeable value within an expression, while a constant is a fixed, unchanging value.
How do I simplify an expression?
+
To simplify an expression, follow the rules of precedence (PEMDAS/BODMAS), combine like terms, and eliminate unnecessary parentheses while preserving the order of operations.
Why is understanding the structure of expressions important?

+
Understanding structure allows you to manipulate expressions correctly, interpret their meaning, and recognize how different parts interact to form a cohesive mathematical or linguistic concept.