5 Essential Tips for Partial Fraction Decomposition Mastery
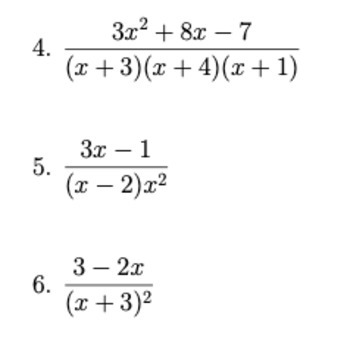
Partial fraction decomposition is a fundamental technique in algebra, precalculus, and calculus that often leaves students and professionals scratching their heads. Whether you're integrating complex rational functions or simplifying algebraic expressions, understanding partial fractions is essential for those tackling higher-level mathematics or engineering problems. This guide will unveil 5 essential tips to not only master partial fraction decomposition but to also enhance your problem-solving skills across various fields of study.
Understanding the Basics of Partial Fraction Decomposition


Partial fraction decomposition involves breaking down a rational function into a sum of simpler fractions. This technique is particularly useful when dealing with improper fractions or to make integration manageable. Here's how it typically works:
- Decompose the Rational Function: Start by ensuring the degree of the numerator is less than the denominator. If it's not, perform polynomial division first.
- Identify Types of Factors in the Denominator:
- Linear factors (e.g., (x - a))
- Repeated linear factors (e.g., (x - a)^2)
- Quadratic or higher degree irreducible factors (e.g., x^2 + bx + c)
- Form the Partial Fractions: Based on the denominator factors, set up the form for the partial fractions. For example:
Denominator Partial Fraction Form Linear factor (x - a) A/(x - a) Repeated linear factor (x - a)^2 A/(x - a) + B/(x - a)^2 Irreducible quadratic x^2 + bx + c (Ax + B)/(x^2 + bx + c) 
Tip 1: Master Polynomial Division


Before you dive into partial fractions, make sure you are adept at polynomial division. This skill is crucial when the degree of the numerator is not less than the denominator:
- Long Division: Traditional method where you divide the leading term of the numerator by the leading term of the denominator, multiply, subtract, and repeat until the degree of the remainder is less than the denominator.
- Synthetic Division: A faster method for polynomials with linear factors, useful for repeated roots.
✏️ Note: Remember that the quotient from polynomial division will become a polynomial added to the sum of the partial fractions.
Tip 2: Identify All Possible Factors Correctly


Correctly identifying the type of factors in the denominator is key to setting up the partial fractions correctly. Here's what to do:
- Factorize the Denominator: Use techniques like the quadratic formula or synthetic division to break down polynomials into their fundamental factors.
- Distinguish Between Factors: Understand the difference between linear, repeated linear, and quadratic factors, as each type will dictate the form of the partial fractions.
- Multiple Roots: Pay special attention to repeated roots, as they require additional terms in the partial fractions.
Tip 3: Set Up and Solve the System of Equations


Once the partial fractions are set up, the next step is to solve for the unknown coefficients. Here's a systematic approach:
- Formulate the Equations: Use the common denominator method or strategic substitution to create a system of equations.
- Solve the System: Solve this system either by substitution, elimination, or using matrices if the system is large.
Here are some strategies for solving:
| Method | Application |
|---|---|
| Substitution | Substitute convenient values into the equation to make some terms zero, simplifying calculations. |
| Elimination | Use algebraic manipulations to eliminate variables, gradually reducing the system. |
| Matrices | Utilize Gaussian elimination or matrix inversion for complex systems of equations. |
Tip 4: Practice with Various Types of Rational Functions


Mastery in partial fraction decomposition comes from varied practice. Here's how you can sharpen your skills:
- Linear Factors: Start with simpler decompositions where denominators are linear factors.
- Quadratic Factors: Progress to problems with irreducible quadratic factors.
- Multiple Roots: Practice with denominators containing repeated linear factors.
- Mixed Factors: Combine different types of factors to develop comprehensive understanding.
💡 Note: Exposure to a wide array of problem sets will improve your ability to recognize and approach different scenarios in partial fraction decomposition.
Tip 5: Utilize Technology for Verification and Insight


While manual solving is essential, technology can provide insights and verification:
- Software and Calculators: Use tools like WolframAlpha, Mathcad, or TI-Nspire CX CAS for decomposition and to check your results.
- Symbolic Algebra Systems: Programs like Mathematica or Maple can solve and manipulate symbolic expressions, offering a quick way to verify your work.
- Graphing: Visualize the original function and its decomposed parts for a deeper understanding of the process.
By following these five tips, you are well on your way to mastering partial fraction decomposition. Remember, the journey to mastery involves not just understanding the theory but also practicing the technique in various contexts. Incorporating technology for verification and exploring a diverse set of problems will round out your skillset, making partial fractions a tool you can confidently wield in any mathematical challenge.
What is the purpose of partial fraction decomposition?

+
The primary goal of partial fraction decomposition is to simplify integration and algebraic manipulation by breaking down a complex rational function into simpler, manageable fractions.
Can partial fraction decomposition be used with trigonometric functions?

+
Yes, although it’s less common. Trigonometric functions can be transformed into rational functions using substitution (like turning tangents into fractions), allowing for the use of partial fractions.
What should I do if the degree of the numerator is equal to or greater than the degree of the denominator?

+
Perform polynomial long division to simplify the expression. The quotient becomes a polynomial term, and the remainder is what you decompose using partial fractions.
How can I check if my partial fraction decomposition is correct?

+
You can manually recombine the fractions to verify if they match the original rational function, or use software like WolframAlpha or Maple for quick verification.