Transform Your Understanding: Parent Graphs and Transformations Guide

Transforming your understanding of parent graphs and functions is like unlocking a key set of tools in your mathematical toolbox. This guide will provide an in-depth exploration of parent functions, their transformations, and how they relate to graphing and analysis in mathematics. Whether you're a student, educator, or math enthusiast, understanding these concepts will enhance your grasp of algebra, calculus, and beyond.
The Fundamentals of Parent Functions
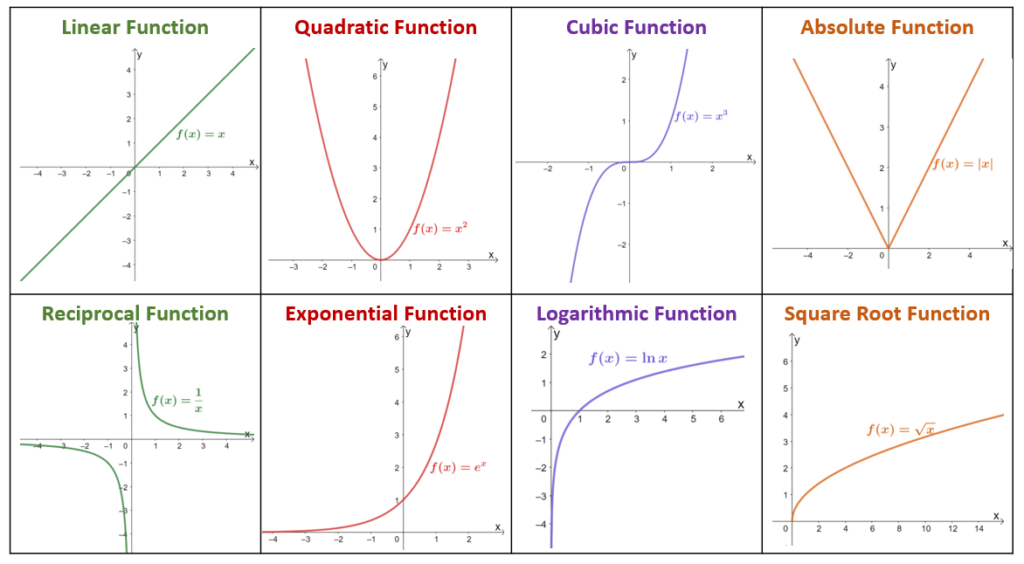
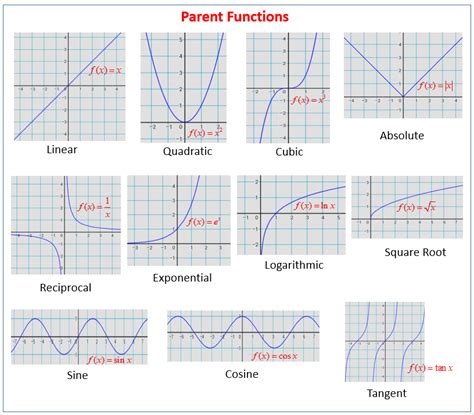
A parent function serves as the most basic form of a function family, representing the simplest version of a graph before any transformations are applied. Here are some of the most common parent functions:
- Linear Function: ( y = x )
- Quadratic Function: ( y = x^2 )
- Cubic Function: ( y = x^3 )
- Absolute Value Function: ( y = |x| )
- Exponential Function: ( y = a^x ) where ( a > 0 )
- Logarithmic Function: ( y = \log_b(x) ) where ( b > 1 )
- Square Root Function: ( y = \sqrt{x} )
- Reciprocal Function: ( y = \frac{1}{x} )

Understanding Transformations
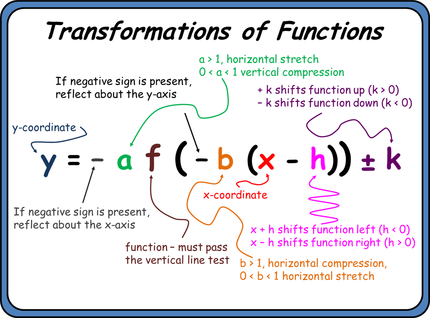
Transformations change the parent graph in four main ways: translation, reflection, dilation (scaling), and rotation. Let’s break these down:
Translations

- Horizontal Translation: If ( f(x) \rightarrow f(x - h) ), the graph shifts right by ( h ) units. If ( h < 0 ), it shifts left.
- Vertical Translation: If ( f(x) \rightarrow f(x) + k ), the graph shifts up by ( k ) units. If ( k < 0 ), it shifts down.
📘 Note: Remember, when shifting horizontally, the sign changes; negative h means move left!
Reflections

- Reflection over the x-axis: ( f(x) \rightarrow -f(x) )
- Reflection over the y-axis: ( f(x) \rightarrow f(-x) )
Dilations (Scaling)

- Vertical Dilation: ( f(x) \rightarrow a \cdot f(x) ). If ( a > 1 ), the graph stretches vertically. If ( 0 < a < 1 ), it compresses.
- Horizontal Dilation: ( f(x) \rightarrow f\left(\frac{x}{b}\right) ). If ( b > 1 ), the graph compresses horizontally; if ( 0 < b < 1 ), it stretches.
Rotation

Rotations are less common in standard algebra but involve rotating the graph around a point or axis. For example, rotating around the origin could transform ( f(x) \rightarrow x - f(x) ), essentially exchanging ( x ) and ( y ).
Applying Transformations

To apply transformations, we must follow these steps:
- Identify the parent function.
- Apply the transformations in the following order: Horizontal shifts, Vertical shifts, Vertical scaling, Horizontal scaling, Reflections, and Rotations.
For instance, let's transform the parent quadratic function f(x) = x^2 with the function g(x) = 2(x - 1)^2 + 3 :
- The parent function is f(x) = x^2 .
- Horizontal Shift: The shift by 1 to the right transforms f(x) to f(x - 1) , giving f(x) = (x - 1)^2 .
- Vertical Shift: Shifts the function up by 3 units, f(x) = (x - 1)^2 + 3 .
- Vertical Scaling: The 2 outside the parentheses stretches the graph vertically by a factor of 2, resulting in f(x) = 2(x - 1)^2 + 3 .
⚠️ Note: The order of applying transformations is crucial for the correct final shape of the graph.
Advanced Transformations

Some transformations can get quite complex, especially when dealing with multiple steps or non-standard functions:
- Non-linear transformations: Functions like ( y = \log_2(\sqrt{x}) ) introduce new challenges.
- Polynomial transformations: Functions like ( y = (x - 2)^3 - 1 ) require careful consideration of cubic behavior.
- Trigonometric transformations: For instance, ( y = \sin(2x + \pi) ) would involve both horizontal and vertical shifts, as well as amplitude changes.
Conclusion
Parent graphs and transformations are fundamental concepts that help in visualizing, analyzing, and working with a wide array of mathematical functions. By mastering these concepts, you gain the ability to predict how functions will look under various conditions, enabling deeper understanding in calculus, solving equations, and beyond. Each transformation provides a tool to modify the basic behavior of functions, opening up a world of possibilities in problem-solving and mathematical modeling.
What is the difference between horizontal and vertical translation?

+
Horizontal translation involves shifting the graph along the x-axis, while vertical translation shifts the graph along the y-axis.
How does the sign of the constant affect the direction of a translation?

+
A positive constant in the translation formula moves the graph to the right or up, while a negative constant shifts it left or down.
Why is the order of transformations important?

+
The order of transformations determines the final shape and position of the graph since each step affects how the next transformation is applied.