Master Parent Function Transformations: Free Worksheet Included

Transforming parent functions is an essential skill in algebra and precalculus that helps students understand how changes in function parameters influence their graphical representation. In this blog post, we'll delve into the concept of parent function transformations, explore different types of transformations, and provide you with practical tips on mastering these concepts. We've also created a comprehensive worksheet to help solidify your understanding through practice.
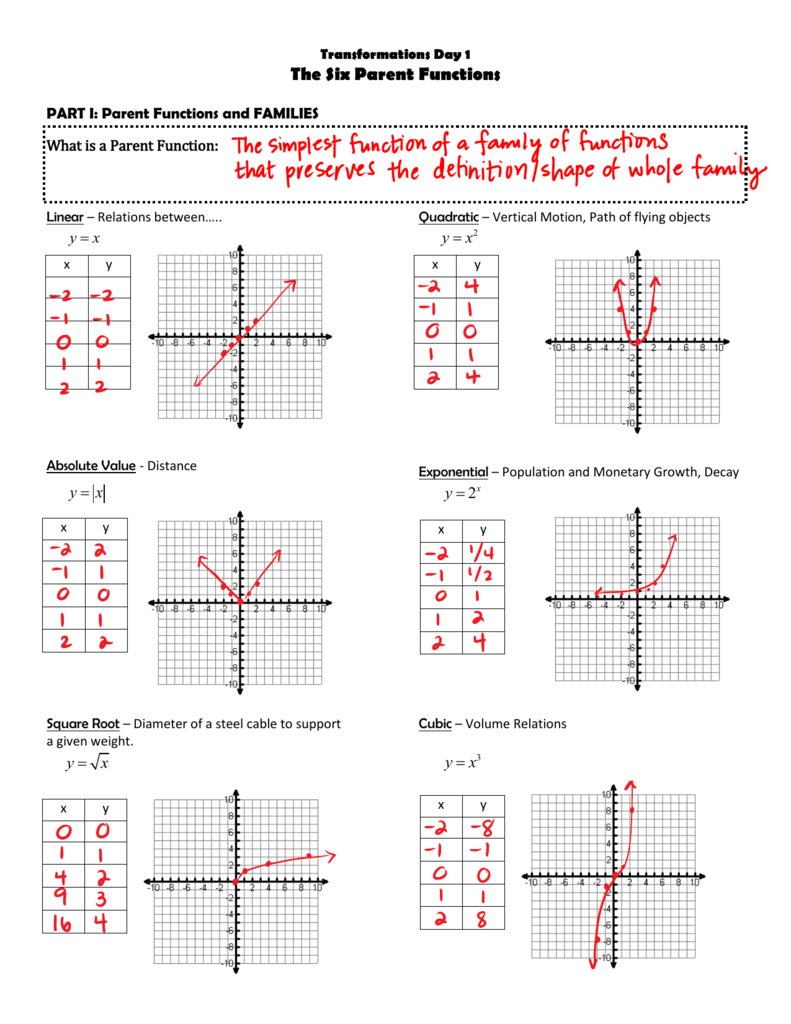
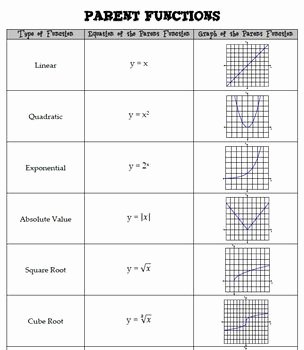
Understanding Parent Functions

Parent functions are the simplest form of a function within their family. Here are some key parent functions:
- Linear Function - f(x) = x
- Quadratic Function - f(x) = x²
- Cubic Function - f(x) = x³
- Square Root Function - f(x) = √x
- Exponential Function - f(x) = ex
📝 Note: The transformation properties apply to all functions but for simplicity, we focus on these common parent functions.
Types of Transformations

When transforming parent functions, there are four primary types of changes you can make:
Vertical Translation

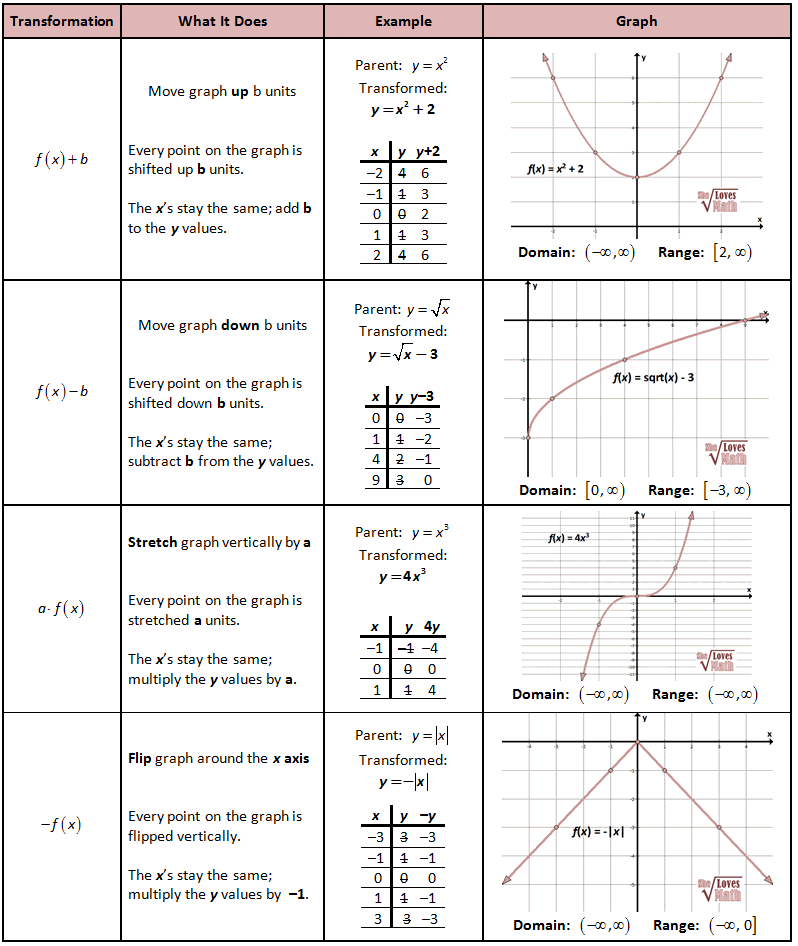
Vertical translation shifts the graph of the function up or down. For a function f(x), the transformation y = f(x) + c moves the graph:
- Up by c units if c is positive.
- Down by c units if c is negative.
Horizontal Translation

Horizontal translation shifts the graph of the function left or right. For a function f(x), the transformation y = f(x - c) moves the graph:
- Right by c units if c is positive.
- Left by c units if c is negative.
Reflections
Reflections transform the graph by flipping it:
- y = -f(x) reflects over the x-axis.
- y = f(-x) reflects over the y-axis.
Dilation

Dilations stretch or compress the graph:
- y = af(x) vertically stretches (if a > 1) or compresses (if 0 < a < 1) the function.
- y = f(bx) horizontally stretches (if 0 < b < 1) or compresses (if b > 1) the function.
⚠️ Note: Vertical transformations involve changing the y-values, whereas horizontal transformations involve changing the x-values.
Combining Transformations
When combining transformations, the order matters:
- Reflections
- Horizontal Stretching/Compression
- Horizontal Translation
- Vertical Stretching/Compression
- Vertical Translation
The transformations can be described in a single equation:
y = a * f[b(x - c)] + d
- a - vertical stretch/compression
- b - horizontal stretch/compression
- c - horizontal translation
- d - vertical translation
| Transformation Type | Formula | Description |
|---|---|---|
| Vertical Translation | y = f(x) + d | Moves graph up or down by d |
| Horizontal Translation | y = f(x - c) | Moves graph left or right by c |
| Vertical Reflection | y = -f(x) | Reflects graph over the x-axis |
| Horizontal Reflection | y = f(-x) | Reflects graph over the y-axis |
| Vertical Stretch/Compress | y = a * f(x) | Stretches or compresses vertically by factor a |
| Horizontal Stretch/Compress | y = f(b * x) | Stretches or compresses horizontally by factor b |

🔧 Note: When combining transformations, each change affects how subsequent transformations will look. The order of operations influences the final graph.
Tips for Mastering Transformations

- Practice Visualization: Try to visualize the graph moving or changing as you apply transformations.
- Use Graphing Calculators: Utilize graphing calculators to confirm your transformations and see them in action.
- Understand Function Families: Get familiar with how different families of functions respond to various transformations.
- Work Backwards: Sometimes, working from the transformed graph back to the parent function helps solidify understanding.
Mastering parent function transformations involves understanding the basic rules of algebraic manipulations, visualizing changes in graphs, and practicing until these operations become second nature. Here's what we've covered:
- An introduction to parent functions and why they are foundational in algebra and precalculus.
- The different types of transformations including vertical and horizontal shifts, reflections, and dilations.
- How to combine multiple transformations and the correct order to apply them.
- Practical tips for mastering these concepts through visualization, calculator use, and understanding function families.
Remember, the journey of learning these transformations doesn't end here. The more you practice, the more intuitive these transformations will become. With time, you'll develop an innate understanding of how functions behave when modified, which is crucial for higher-level math courses and real-world problem-solving.
What are parent functions?

+
Parent functions are the basic forms of functions in their respective families, such as linear functions, quadratic functions, etc. They serve as the starting point for all other functions in the same family through transformations.
Why is the order of transformations important?
+
The order matters because each transformation changes the function, affecting how the next transformation will impact the graph. Applying transformations in the correct order ensures that the graph is correctly modified according to the mathematical rules.
How can I practice function transformations?

+
You can practice by using graphing software or calculators to visualize the changes, drawing graphs by hand, working through worksheets, and solving transformation problems in textbooks or online resources.
Do all functions behave the same way under transformations?
+
While the basic rules of transformations apply to all functions, the outcome might look different due to the original shape and nature of the function. However, the transformation principles remain consistent across all function families.