Parent Functions and Transformations: Simplified Worksheet Guide

In this comprehensive guide, we'll explore the fascinating world of parent functions and their transformations. This is designed to provide educators and students with an accessible, step-by-step understanding of how functions can be altered to create various mathematical expressions. Whether you're teaching algebra or studying for an exam, this guide will streamline your learning process, making complex concepts much more straightforward.
Understanding Parent Functions

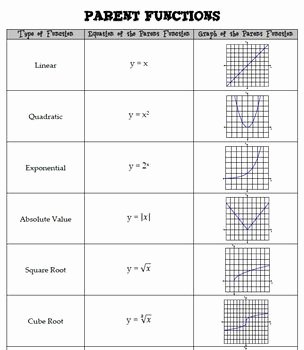
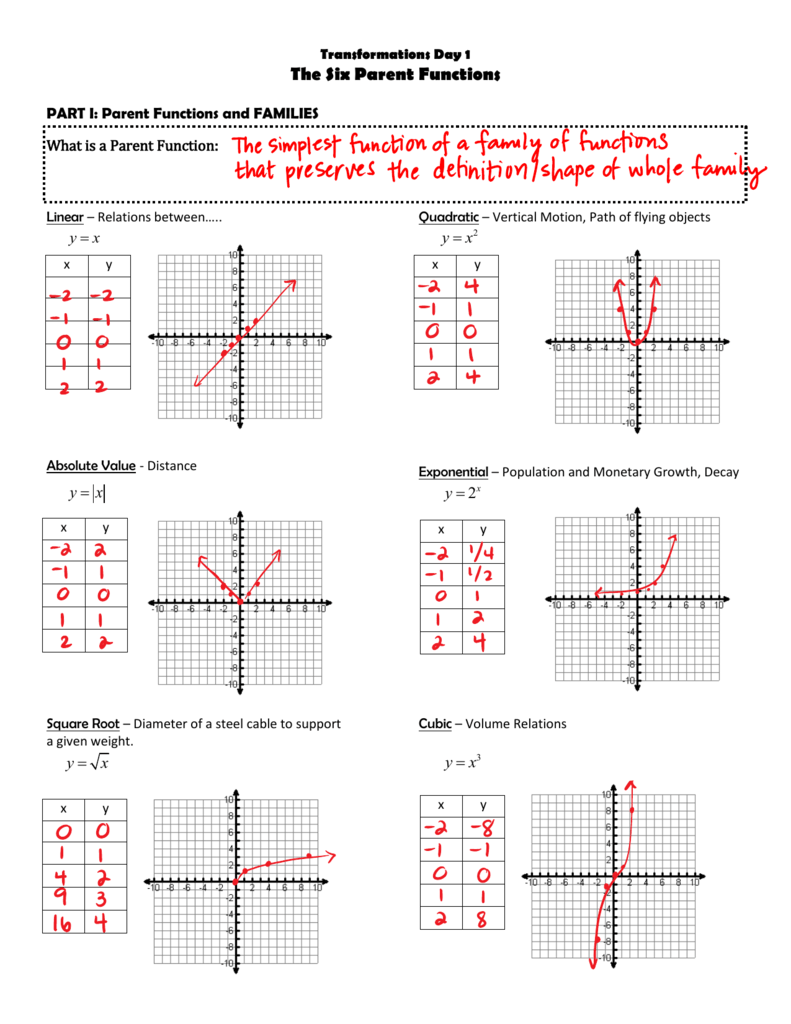
Parent functions are the basic form of functions from which all other functions of their kind can be derived through transformations. They are the simplest functions in their class:
- Linear Parent Function: ( f(x) = x )
- Quadratic Parent Function: ( f(x) = x^2 )
- Cubic Parent Function: ( f(x) = x^3 )
- Square Root Parent Function: ( f(x) = \sqrt{x} )
- Absolute Value Parent Function: ( f(x) = |x| )
- Exponential Parent Function: ( f(x) = b^x ) where ( b > 0, \neq 1 )
- Logarithmic Parent Function: ( f(x) = \log_b(x) ) where ( b > 0, \neq 1 )
These parent functions serve as a foundation for understanding how all other functions in their respective families behave.
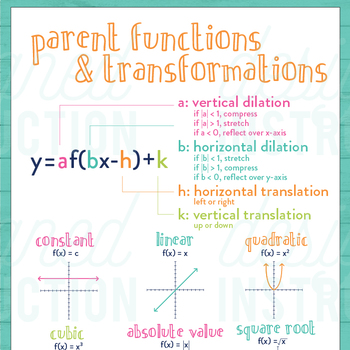
Types of Transformations

There are four primary types of transformations applied to functions:
- Vertical Shifts: Moving the graph of a function up or down.
- Horizontal Shifts: Moving the graph left or right.
- Reflections: Flipping the graph over an axis.
- Stretches and Compressions: Stretching or compressing the graph vertically or horizontally.
Understanding these transformations allows for the creation of a variety of functions from just a handful of parent functions.
Worksheet Guide for Teaching Transformations

To help students grasp these concepts, here are some exercises you might include in a worksheet:
Vertical and Horizontal Shifts

- Given ( f(x) = x^2 ), describe how the function would be shifted to form ( g(x) = (x-3)^2 ) and ( h(x) = x^2 + 4 ).
💡 Note: A horizontal shift means moving all x-coordinates left or right, and a vertical shift moves all y-coordinates up or down.
- Graph ( f(x) = \sqrt{x} ) and then shift it left by 2 units and down by 1 unit. Describe the new function.
Reflections

- Reflect ( f(x) = x^3 ) over the y-axis and over the x-axis. What are the new functions?
Stretches and Compressions
| Transformation | Vertical | Horizontal |
|---|---|---|
| Stretch | ( g(x) = kf(x) ), ( k > 1 ) | ( h(x) = f(\frac{x}{a}) ), ( 0 < a < 1 ) |
| Compression | ( g(x) = kf(x) ), ( 0 < k < 1 ) | ( h(x) = f(\frac{x}{a}) ), ( a > 1 ) |

- Given ( f(x) = |x| ), create a function that is both vertically stretched by a factor of 3 and reflected over the x-axis.
- Graph ( f(x) = e^x ) and then compress it horizontally by a factor of 2.
Combining Transformations

- Transform ( f(x) = \log_b(x) ) by shifting left 1 unit, reflecting over the x-axis, and compressing vertically by a factor of 1⁄2. Write the new function.
This approach to transformations can help students visualize how different alterations affect the shape, position, and characteristics of parent functions.
Worksheet Tips
Here are some additional tips to enhance your worksheet:
- Provide blank graphs alongside each problem to encourage sketching.
- Incorporate multiple-choice questions to assess comprehension quickly.
- Include a section for “Transformation Story” where students describe a journey from one function to another through a series of transformations.
Understanding parent functions and their transformations not only facilitates algebraic manipulation but also deepens students' appreciation of how functions relate to each other. This worksheet guide simplifies this process, making it approachable for both educators and students.
Summary of Key Points

This guide has illuminated how various transformations alter the shape, position, and behavior of parent functions. By exploring vertical and horizontal shifts, reflections, stretches, and compressions, we’ve shown how a basic function can be modified to represent a wide array of mathematical models. Emphasizing visual representation through graphs and story problems makes these transformations more intuitive and engaging for learners.
What is the purpose of studying parent functions?

+
Parent functions provide a baseline for understanding the behaviors of related functions through transformations. They simplify the learning process by showing how a single function can be modified to explore a whole family of functions.
How do I know if a function has been horizontally or vertically shifted?

+
If you see an operation on ( x ) inside the function, like ( f(x) + c ) or ( f(x + c) ), it indicates a vertical or horizontal shift, respectively. The sign tells the direction.
Why are reflections important in function transformations?

+
Reflections help visualize how functions can change in symmetry or orientation, providing insight into their periodicity, symmetry, and behavior under certain operations.
Can a function undergo multiple transformations at once?
+
Yes, functions can be subject to multiple transformations simultaneously, such as shifts, reflections, stretches, or compressions. This combination allows for the creation of complex functions from simpler ones.


