Parent Functions: Transformations Worksheet With Answers
Understanding the transformations of parent functions is crucial for anyone delving into algebra or calculus. This guide will help you master how these transformations work, providing examples and a detailed worksheet with answers to solidify your understanding.
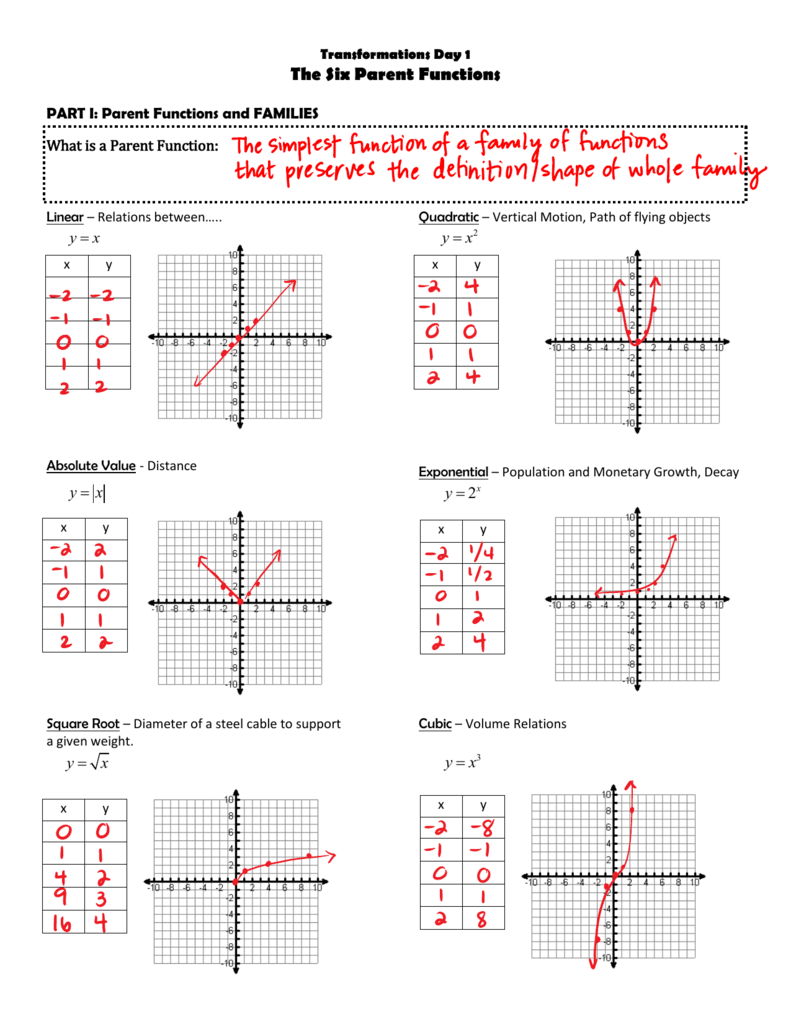
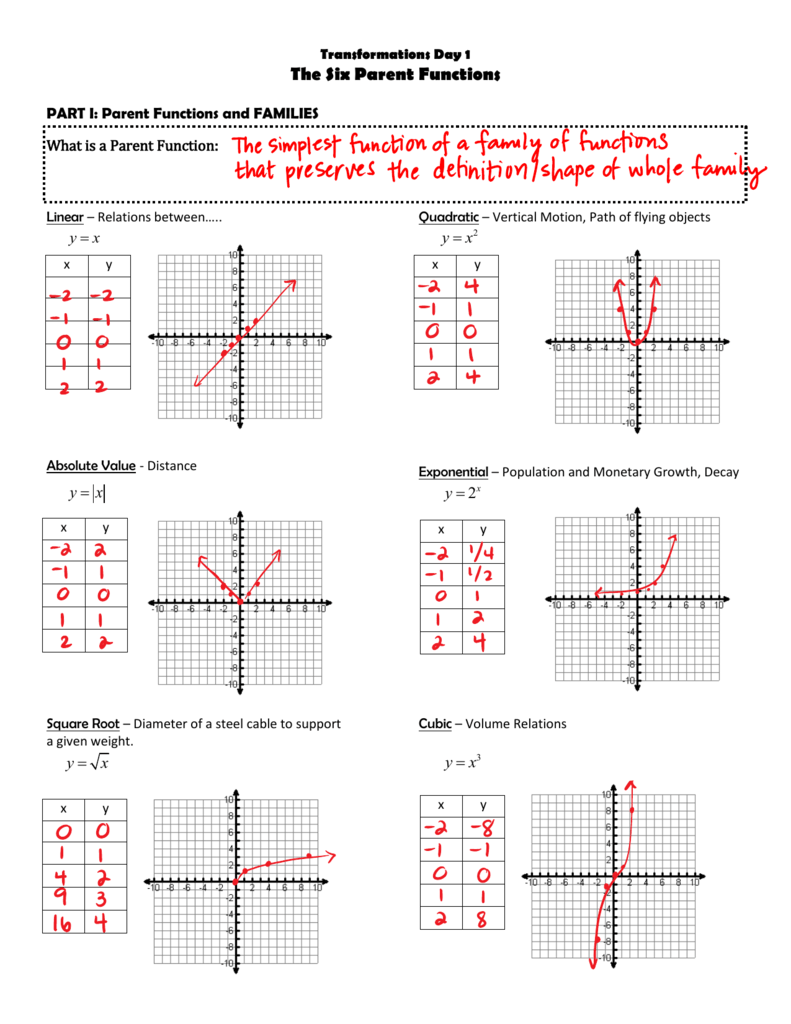
The Basics of Parent Functions

A parent function is the simplest function of a particular type, serving as a blueprint for more complex functions within its family. Here are a few examples:
- Linear Function: f(x) = x
- Quadratic Function: f(x) = x^2
- Cubic Function: f(x) = x^3
Types of Transformations
Transformations of parent functions involve changing the function's graph in several ways:
1. Translations

Translations move the graph without changing its size or shape:
- Vertical Translation: ( f(x) + c ) shifts the graph up by ( c ) units.
- Horizontal Translation: ( f(x - h) ) shifts the graph right by ( h ) units.
2. Reflections

Reflections flip the graph:
- Reflection Over the x-axis: ( -f(x) )
- Reflection Over the y-axis: ( f(-x) )
3. Stretches and Compressions

These change the graph’s steepness:
- Vertical Stretch/Compression: ( a \cdot f(x) ) where ( |a| > 1 ) stretches and ( 0 < |a| < 1 ) compresses vertically.
- Horizontal Stretch/Compression: ( f(kx) ) where ( |k| > 1 ) compresses and ( 0 < |k| < 1 ) stretches horizontally.
Worksheet: Transformations of Parent Functions

Here is a worksheet designed to test your understanding of the transformations discussed above. Each problem should be solved with respect to the parent function f(x) .
| Problem | Description | Transformation | Equation |
|---|---|---|---|
| 1 | Shift the parent function f(x) = x^2 up by 3 units. | Vertical Translation | f(x) + 3 = x^2 + 3 |
| 2 | Reflect the parent function f(x) = |x| over the y-axis. | Reflection Over y-axis | f(-x) = |-x| = |x| |
| 3 | Stretch the parent function f(x) = \sqrt{x} by a factor of 2 in the vertical direction. | Vertical Stretch | 2\sqrt{x} |
| 4 | Compress the parent function f(x) = \frac{1}{x} horizontally by a factor of 2. | Horizontal Compression | f(2x) = \frac{1}{2x} |
🏼 Note: Remember that the transformations can be combined, but their order affects the final result.
🎨 Note: When graphing, sketching the transformations step-by-step helps in visualizing the changes.
In mastering these transformations, you'll develop a deeper understanding of how functions behave and evolve. By recognizing these patterns, solving equations or graphing functions becomes more intuitive and efficient. Whether for academic purposes or practical applications in fields like physics or engineering, understanding function transformations provides a valuable toolset for problem-solving and analysis.
What is a parent function?
+
A parent function is the basic or simplest form of a function that represents the core characteristics of a family of functions. It is the function from which all other functions in its family can be derived through transformations.
How does horizontal translation affect a function?
+
Horizontal translation shifts the graph of a function left or right along the x-axis. A function ( f(x - h) ) will shift right by ( h ) units if ( h ) is positive, and left if ( h ) is negative.
Can transformations change the domain or range of a function?

+
Generally, vertical translations and vertical stretches/compressions do not change the domain, but they can alter the range. Horizontal transformations might change both domain and range, depending on the function and the nature of the transformation.