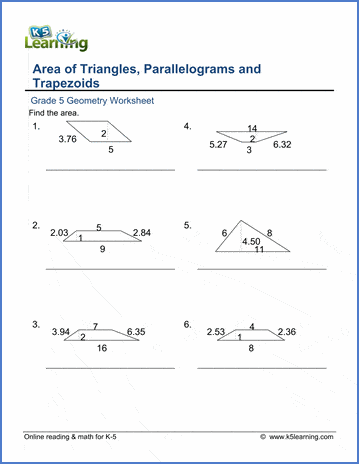
5 Tips for Mastering Parallelograms Geometry Worksheet

Delving into the world of geometry can be both exhilarating and challenging. Among the various shapes you encounter, parallelograms stand out due to their unique properties and the versatility they offer in problem-solving. Whether you're a student grappling with geometry worksheets or an educator looking to enrich your lesson plans, understanding how to master problems related to parallelograms is essential. This comprehensive guide will provide you with five expert tips to help you navigate through parallelogram geometry exercises with confidence and ease.
Understanding the Basics of Parallelograms

Before diving into advanced techniques, it’s crucial to revisit the basics:
- Definition: A parallelogram is a quadrilateral with opposite sides parallel and equal in length.
- Properties:
- Opposite sides are equal.
- Opposite angles are equal.
- Consecutive angles are supplementary.
- Diagonals bisect each other.
- The sum of the interior angles is 360°.
Embed an image here illustrating a basic parallelogram with labeled parts to aid in visualizing these properties.
Tip 1: Utilize Visualization Techniques

One of the most effective ways to solve geometry problems involving parallelograms is through visualization. Here are some techniques:
- Draw Diagonals: Drawing the diagonals can help you understand the symmetry and establish relationships between angles and sides.
- Use Color Coding: Assign different colors to different elements (angles, sides, diagonals) to better differentiate between them.
- Construct Perpendiculars: Draw perpendicular lines from vertices to opposite sides to reveal more properties or to find areas.
🖌️ Note: Using a ruler and protractor can ensure accuracy in your visualizations, making it easier to analyze the parallelogram.
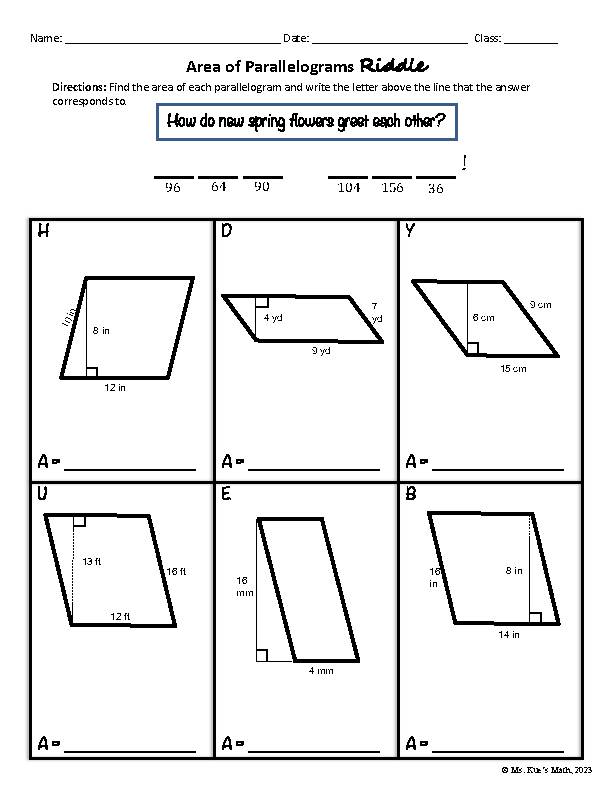
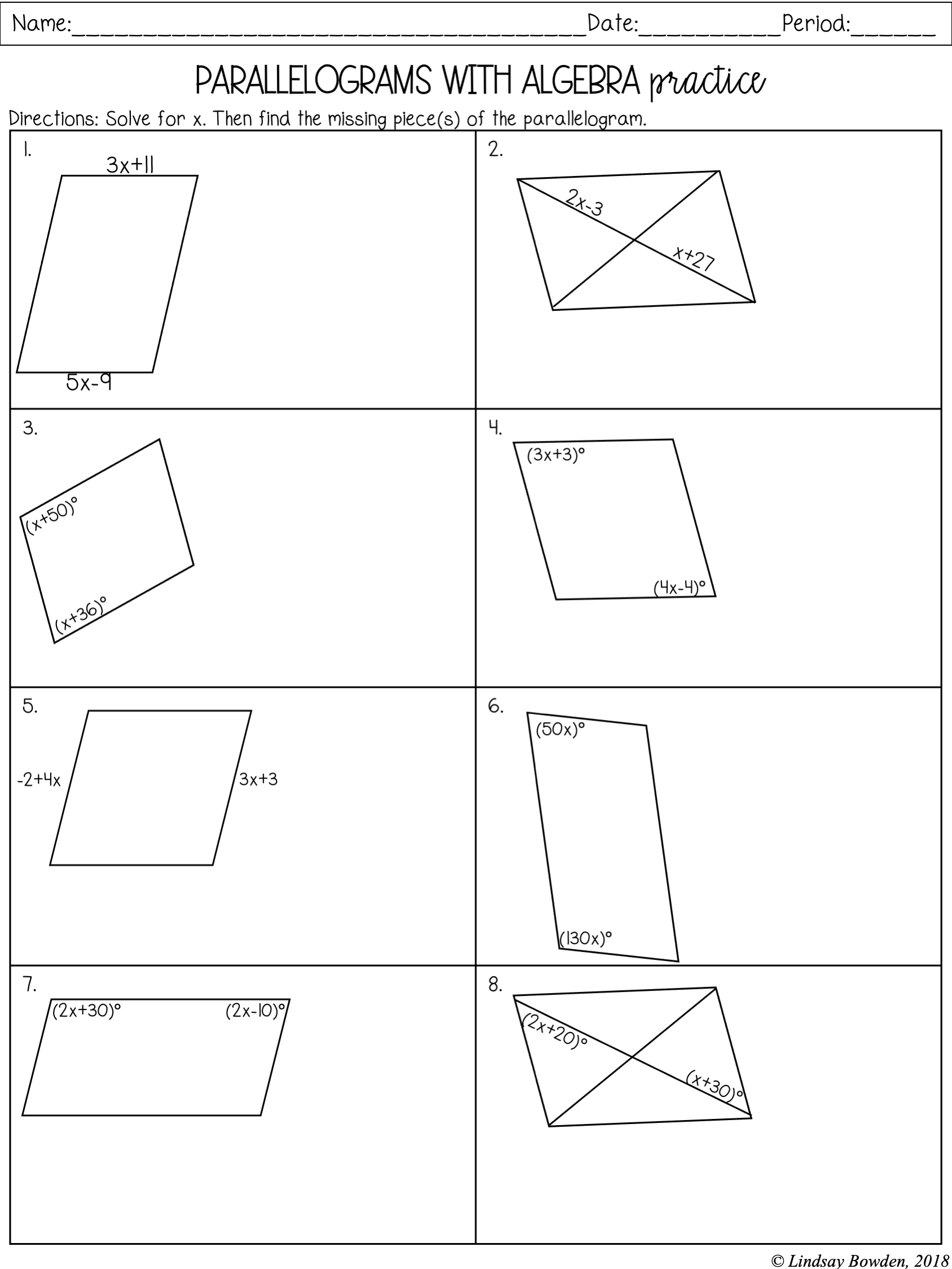
Tip 2: Apply Algebraic Methods
When geometric constructions aren’t enough, algebraic methods can come to the rescue:
- Set Up Equations: Use known properties to create equations that can help solve for unknown angles or sides.
- Use Simultaneous Equations: If you have multiple unknowns, solve them simultaneously using the properties of the parallelogram.
- Area Formulas: Learn different ways to find the area of a parallelogram (e.g., base times height, diagonal times sine of the included angle).
| Formula | Description |
|---|---|
| A = b × h | Area where b is the base and h is the height. |
| A = ab sin(θ) | Area where a and b are sides, and θ is the angle between them. |

📝 Note: Always double-check your equations to ensure they reflect the actual properties of the parallelogram.
Tip 3: Master Trigonometry for Angles and Sides
Trigonometry often plays a key role in solving for angles and side lengths:
- Use the Law of Sines and Cosines: These laws are particularly useful when dealing with non-right angled parallelograms.
- Right Triangle Relationships: If a parallelogram can be split into right triangles, use sine, cosine, and tangent functions to find missing elements.
Tip 4: Incorporate Vector Analysis
Vectors provide a powerful tool in dealing with geometric shapes, especially for proofs and analysis:
- Vector Addition and Subtraction: Use vectors to represent sides, diagonals, and find resultant forces or vectors.
- Perpendicular Vectors: The dot product can help determine when two vectors are perpendicular, which is useful in calculating angles.
Tip 5: Explore Advanced Theorems and Properties

Delving deeper into the world of parallelograms reveals additional insights:
- Varignon’s Theorem: States that the quadrilateral formed by connecting the midpoints of a parallelogram’s sides is itself a parallelogram with an area half that of the original.
- Brahmagupta’s Formula: For cyclic quadrilaterals, but useful for parallelograms too, to find areas without knowing height.
- Ptolemy’s Theorem: Useful in dealing with cyclic quadrilaterals and indirectly helpful with parallelograms.
In summary, mastering parallelograms involves more than just recognizing their basic properties. It requires you to apply visualization, algebraic, trigonometric, and even vector analysis techniques. With these tips in hand, you're well-equipped to tackle geometry worksheets involving parallelograms with confidence. Whether you're calculating areas, understanding angle relationships, or proving geometric statements, these strategies will provide you with a solid foundation to excel in geometry.
What is the most useful property of a parallelogram in solving geometry problems?

+
The property that diagonals bisect each other is often the most useful as it allows you to relate sides and angles in various ways.
How can I quickly find the area of a parallelogram if I only know the length of the sides?

+
Use the sine formula: A = ab sin(θ), where θ is the angle between two sides of the parallelogram.
Why do we need to use vector analysis in parallelogram geometry?

+
Vector analysis provides a more abstract and powerful way to solve complex problems, especially in proofs, force calculations, and position analysis within the parallelogram.