Parallelogram Proofs Worksheet: Get Free Answers Now
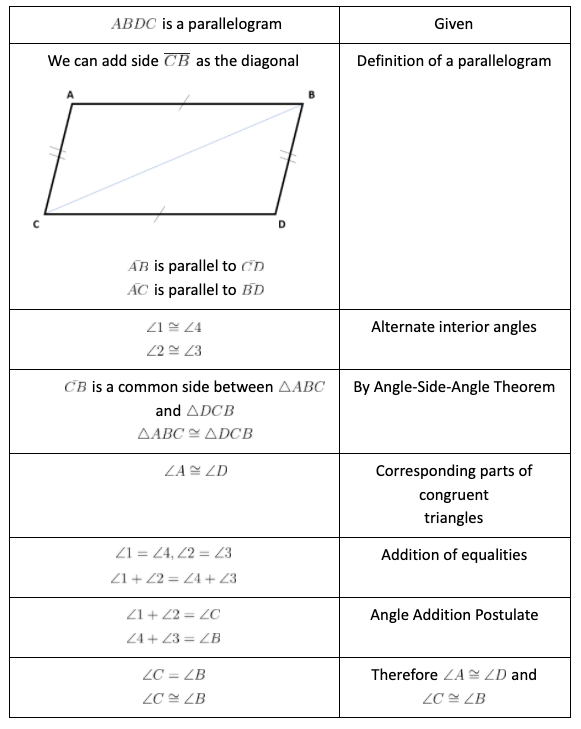
Geometric shapes often seem abstract, but when it comes to parallelogram proofs, they become a playground for mathematical logic and reasoning. A parallelogram is a four-sided plane rectilinear figure with opposite sides parallel, and proving its properties can be both challenging and rewarding. Today, we're diving into the world of parallelogram proofs, offering a comprehensive guide to understanding and solving proofs related to this fascinating quadrilateral.
What is a Parallelogram?
A parallelogram is defined by four key properties:
- Opposite sides are parallel and equal in length.
- Opposite angles are equal.
- Consecutive angles are supplementary (sum up to 180°).
- The diagonals bisect each other.
These properties form the basis for numerous proofs involving parallelograms.
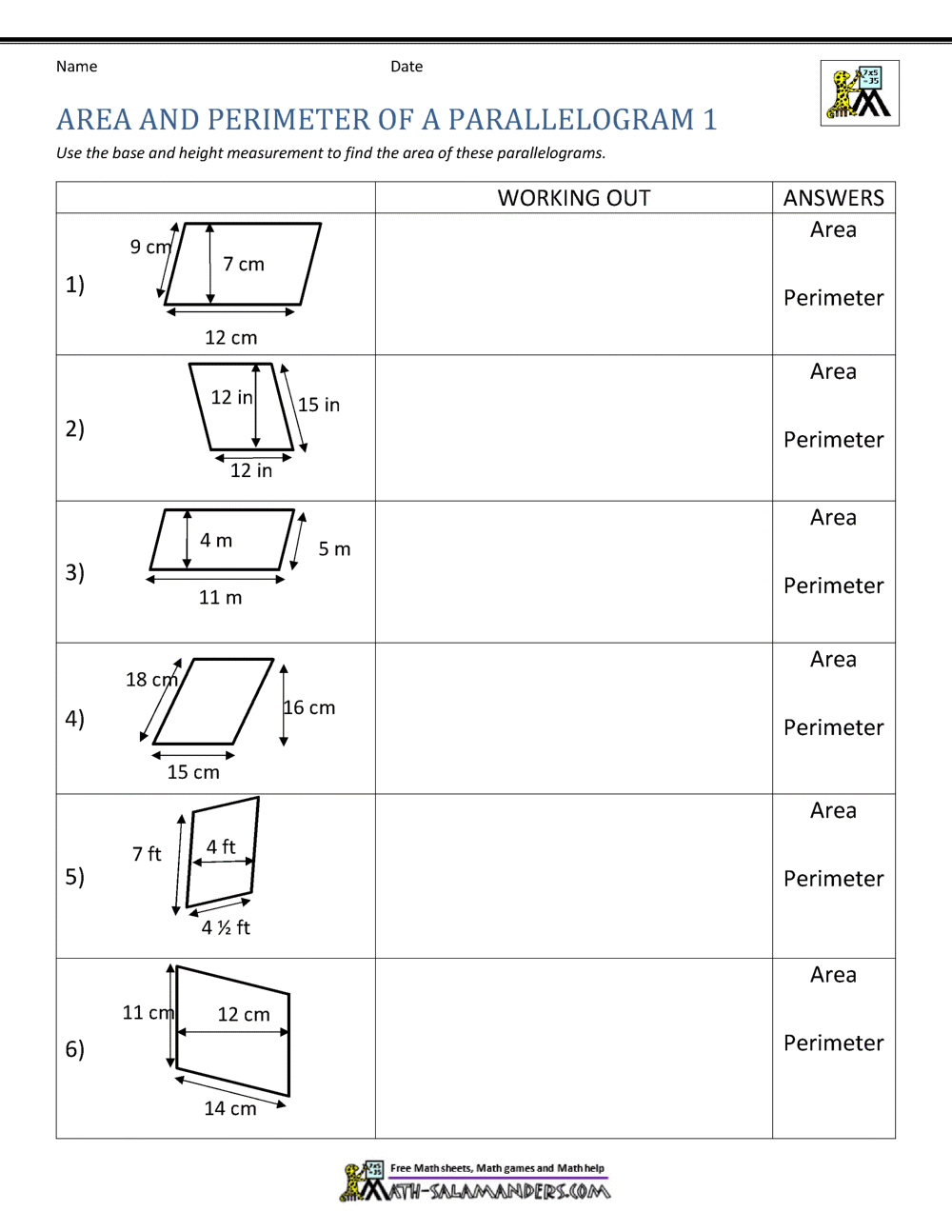
How to Prove a Quadrilateral is a Parallelogram
To establish that a quadrilateral is a parallelogram, you can use the following conditions:
- Both pairs of opposite sides are parallel.
- Both pairs of opposite sides are equal.
- One pair of opposite sides is both parallel and equal.
- Diagonals bisect each other.
- All angles are supplementary.
- One pair of opposite angles is congruent.
Let’s delve into each method of proof with examples.
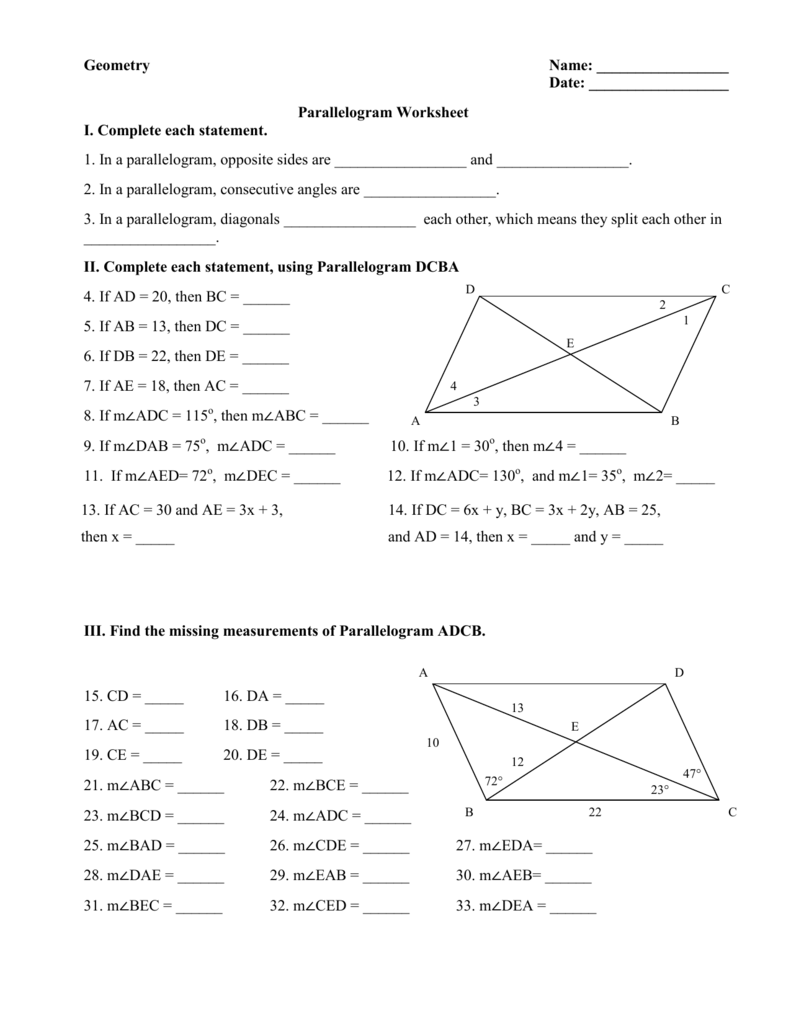
Proof by Opposite Sides Parallel

If both pairs of opposite sides of a quadrilateral are parallel, it is a parallelogram. Here’s how you might prove this:
Example: Given quadrilateral ABCD, if we know that AB||CD and BC||DA, we can conclude ABCD is a parallelogram because this satisfies the first condition.
Proof by Opposite Sides Equal

If both pairs of opposite sides of a quadrilateral are equal, then it is also a parallelogram. Here’s an example:
Example: If AB = CD and AD = BC, then quadrilateral ABCD is a parallelogram by the second condition.
Proof by One Pair Parallel and One Pair Equal

A less common but valid proof involves one pair of sides that are both parallel and equal. Here’s how it could look:
Example: If AB||CD and AB = CD, quadrilateral ABCD is a parallelogram.
Proof by Diagonals Bisecting Each Other

If the diagonals of a quadrilateral bisect each other, then it is a parallelogram:
Example: Given diagonals AC and BD, if point O is such that AO = OC and BO = OD, then quadrilateral ABCD is a parallelogram.
Proof by Supplementary Angles

If the sum of consecutive angles of a quadrilateral equals 180°, then it is a parallelogram:
Example: If ∠A + ∠B = 180° and ∠B + ∠C = 180°, quadrilateral ABCD is a parallelogram.
Proof by Congruent Opposite Angles

If one pair of opposite angles is congruent, then the quadrilateral is a parallelogram:
Example: If ∠A = ∠C, then quadrilateral ABCD is a parallelogram.
Worksheet: Parallelogram Proofs
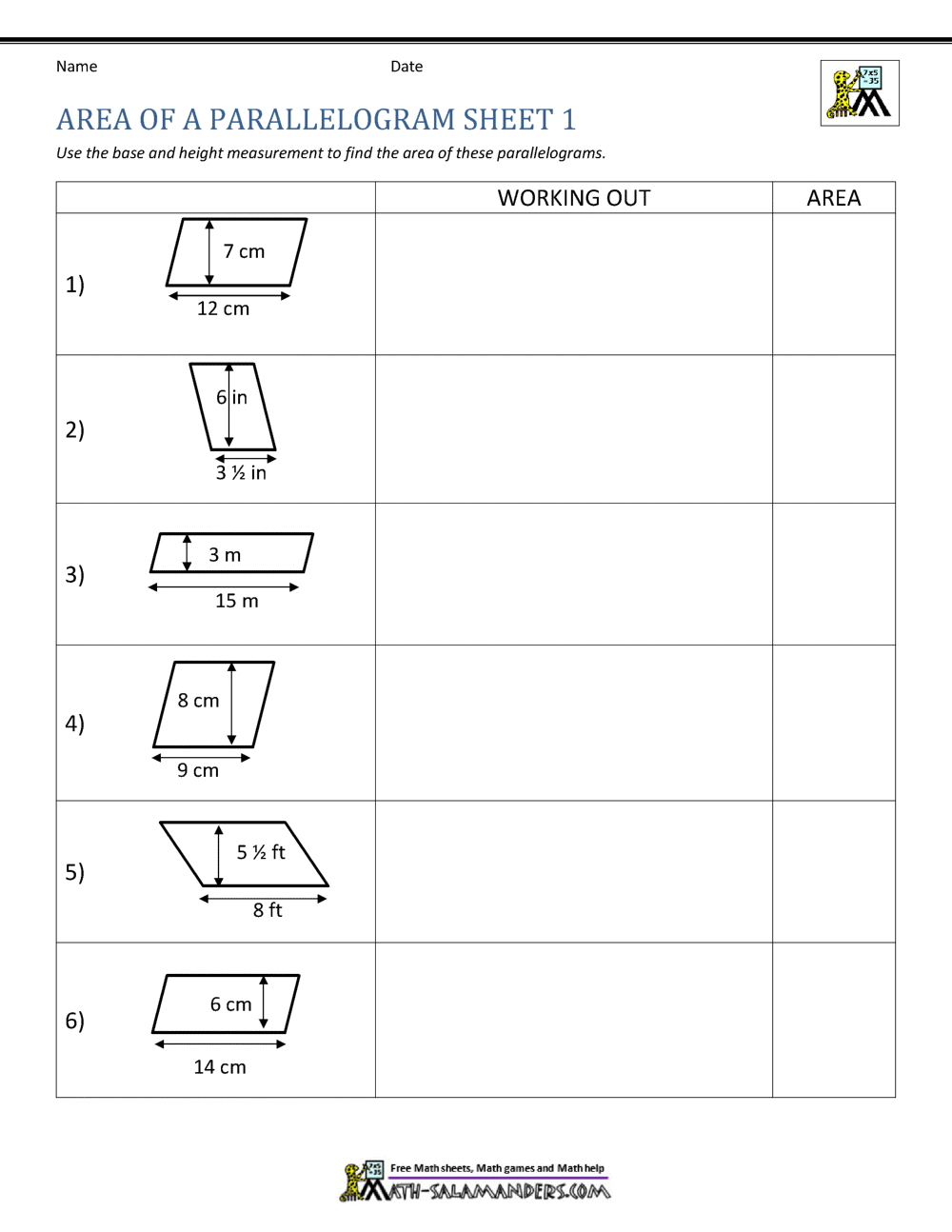
Here’s a short worksheet to practice your parallelogram proof skills:
| Statement | Proof Method | Proof |
|---|---|---|
| ABCD is a quadrilateral where AB = CD and AB||CD | One Pair Parallel and One Pair Equal | Since one pair of sides is both parallel and equal, ABCD is a parallelogram. |
| ABCD has diagonals AC and BD intersecting at point O where AO = OC and BO = OD | Diagonals Bisecting Each Other | By the definition of diagonals bisecting each other, ABCD is a parallelogram. |
| ABCD is a quadrilateral where ∠A + ∠B = 180° and ∠B + ∠C = 180° | Supplementary Angles | Given the supplementary angles, we can conclude ABCD is a parallelogram. |
| ABCD has AB = CD and AD = BC | Opposite Sides Equal | With both pairs of opposite sides equal, ABCD is a parallelogram. |
| ABCD has ∠A = ∠C | Congruent Opposite Angles | If one pair of opposite angles are congruent, ABCD is a parallelogram. |

Common Misconceptions in Parallelogram Proofs
Understanding parallelogram proofs can be tricky due to some common misconceptions:
- Length alone does not make a parallelogram: If you only know the length of opposite sides, you need additional information to prove it’s a parallelogram.
- All rectangles are parallelograms, but not all parallelograms are rectangles: This is a key distinction to keep in mind.
- Diagonals don’t always indicate a parallelogram: The diagonals must bisect each other for the quadrilateral to be a parallelogram.
📝 Note: While some proofs might look similar, they can lead to different conclusions. Always verify each condition carefully.
Strategies for Mastering Parallelogram Proofs

To become proficient in parallelogram proofs, consider the following strategies:
- Visualize: Draw diagrams to help understand the given information.
- Know Your Properties: Memorize the properties of parallelograms and understand how they’re interconnected.
- Practice: Repetition is key in math. Solve as many problems as you can.
- Identify Key Information: Recognize which condition you’re working with to choose the appropriate proof method.
By focusing on these strategies, you'll find that parallelogram proofs become a more intuitive process over time.
Understanding parallelogram proofs opens the door to a deeper appreciation of geometry. Not only do these proofs test your knowledge of basic geometric properties, but they also challenge your logical reasoning and problem-solving skills. Parallelogram proofs are foundational in the realm of mathematics, often paving the way for more complex geometric relationships and theorems. Remember, practice makes perfect. The more you engage with these proofs, the more you'll grow to understand and appreciate the intricate logic that underlies geometric shapes. Keep practicing, and soon, the solutions will not only be clear but also rewarding to uncover.
What is the difference between a parallelogram and a rectangle?

+
A rectangle is a type of parallelogram where all four angles are right angles (90°). While a parallelogram can have any angle as long as opposite sides are parallel and equal, a rectangle is more specific.
Why do I need to learn parallelogram proofs?
+
Parallelogram proofs help you understand properties of shapes, develop logical thinking, and are foundational for other geometric concepts and advanced mathematics.
Can diagonals of a parallelogram be equal?

+
Yes, but only in the case of a rectangle or rhombus, where the diagonals bisect each other at 90°. In a general parallelogram, diagonals are equal only if it’s a rectangle.
How can I remember the conditions for proving a quadrilateral is a parallelogram?

+
Try mnemonic devices like ‘OOPB’ for Opposite sides parallel, Opposite sides equal, One pair parallel and one pair equal, and Properties of diagonals Bisecting each other.