5 Quick Tips for Parallel Lines and Transversals
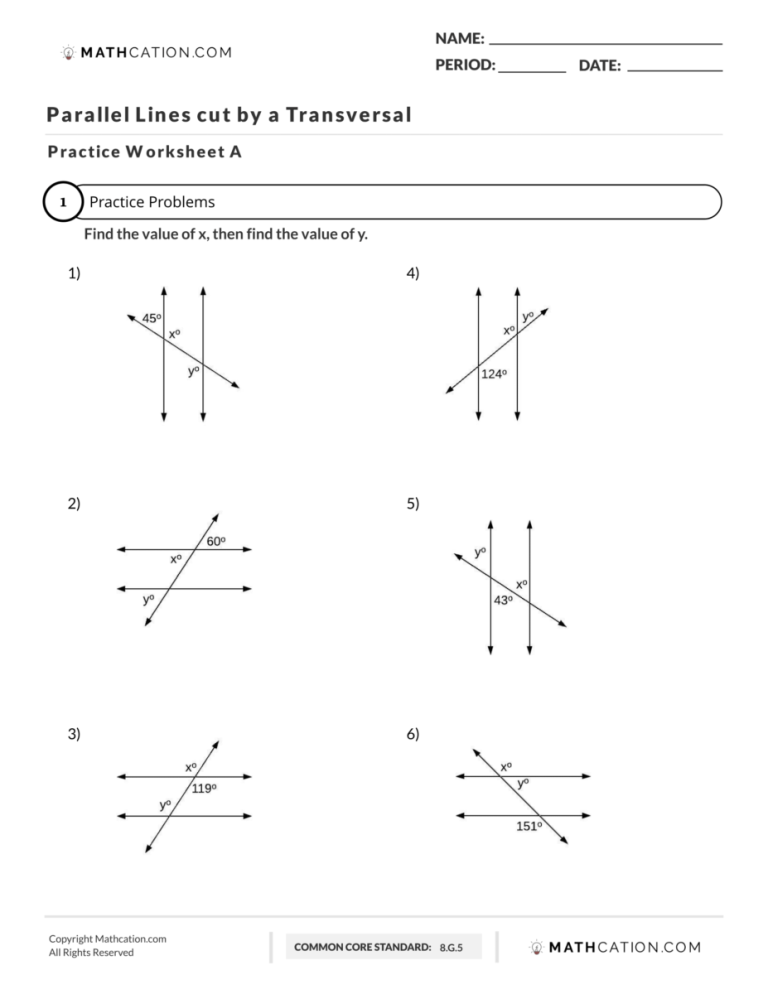
Geometry, often considered a cornerstone of mathematics, offers a fascinating look at the world through shapes and lines. Among the various geometric concepts, parallel lines and their interaction with transversals provide fundamental insights into spatial reasoning and logic. This article delves into five quick tips that can help you grasp these concepts more effectively, ensuring your understanding is not only theoretical but also practical.
Understanding Parallel Lines and Transversals

Before diving into the tips, let’s quickly define what we’re talking about:
- Parallel lines are two lines on the same plane that never meet, maintaining the same distance apart indefinitely.
- A transversal is a line that cuts through two or more other lines. When this line intersects parallel lines, it creates several angles with specific properties.

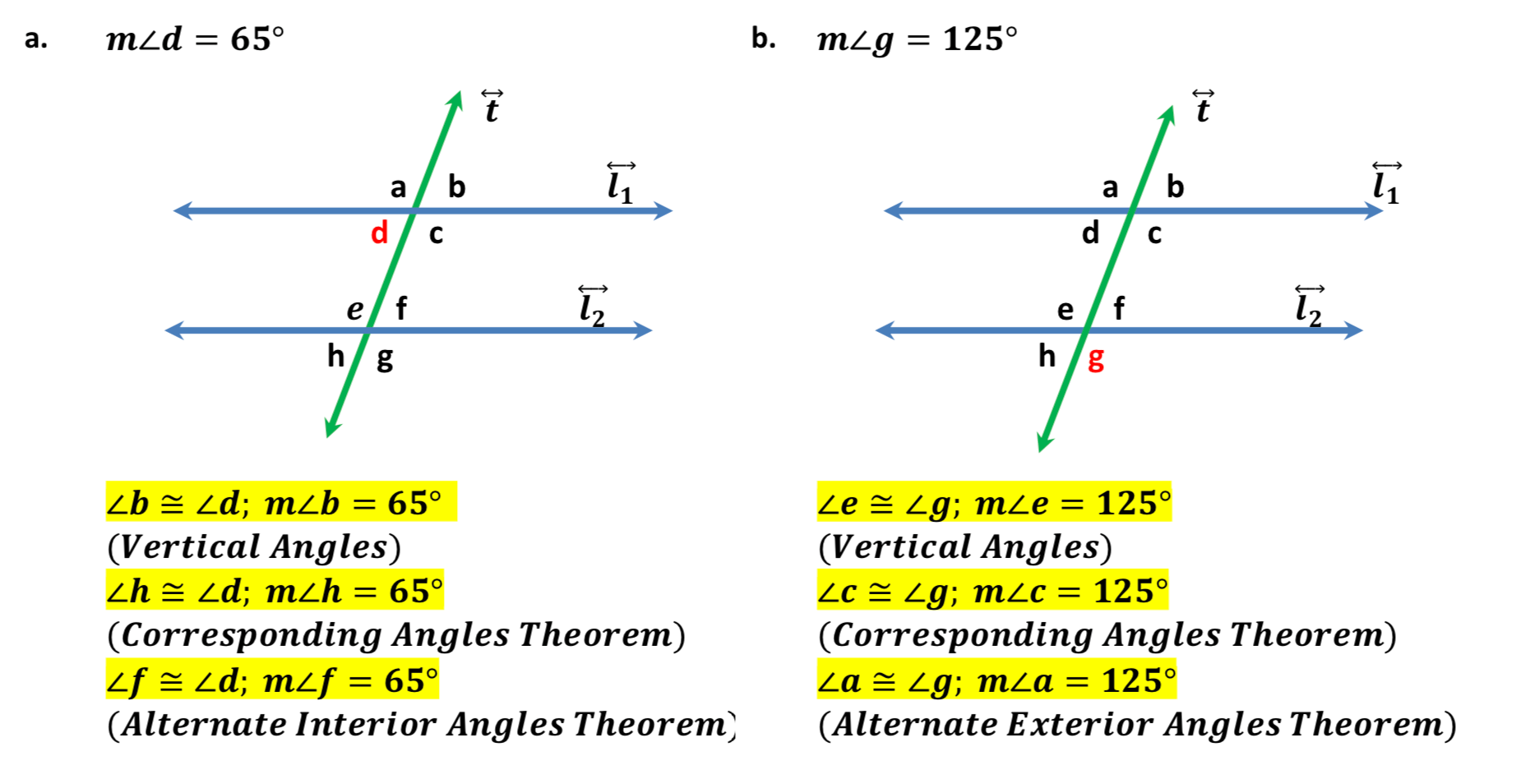
1. Recognize Angle Relationships
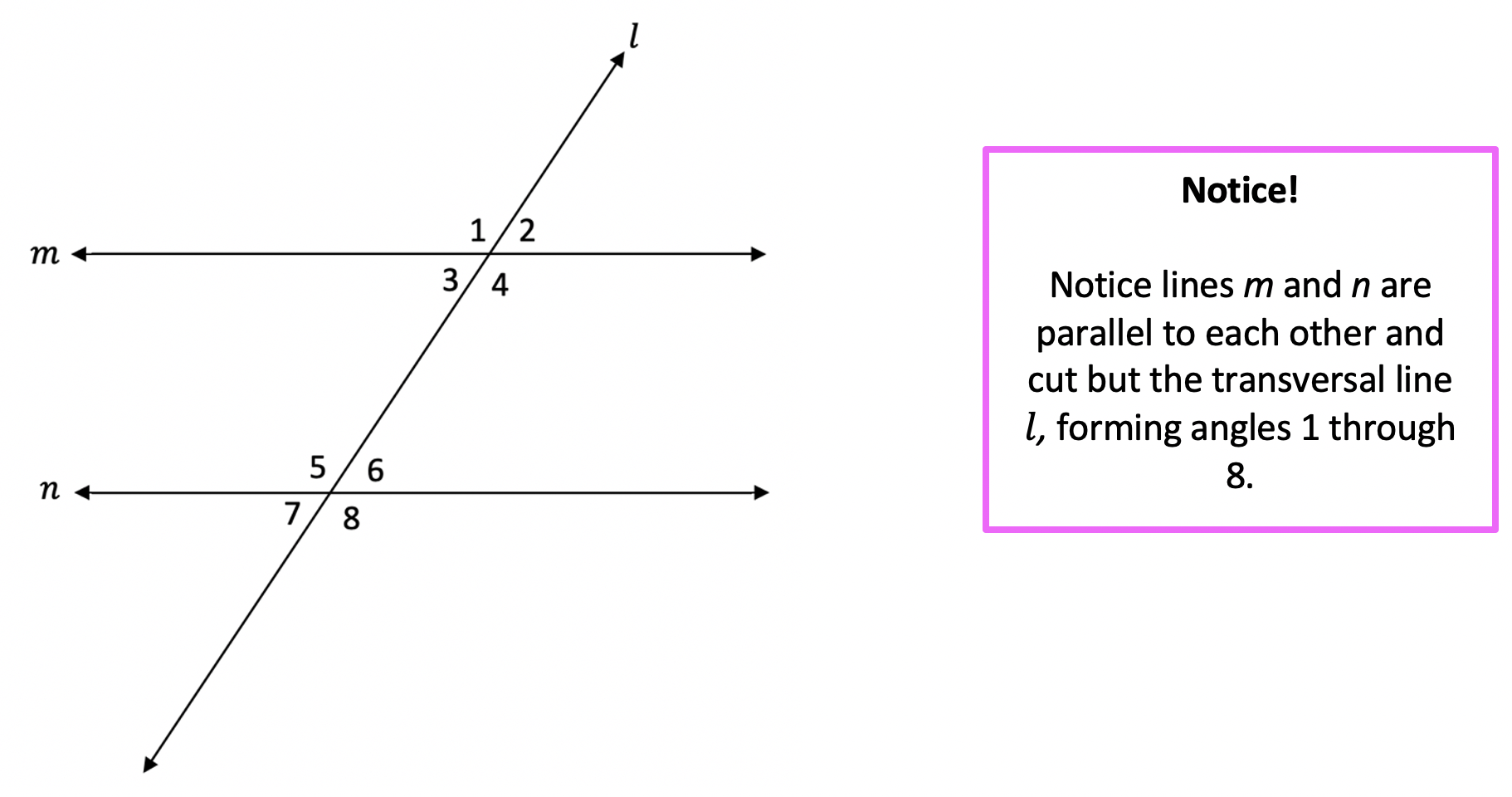
When a transversal cuts parallel lines, it creates:
- Corresponding angles: These angles are in the same position at each intersection, like the top left corners.
- Alternate interior angles: Opposite angles inside the parallel lines.
- Alternate exterior angles: Opposite angles outside the parallel lines.
- Consecutive interior angles: Angles on the same side of the transversal but inside the parallel lines.
Here are the key relationships:
| Relationship | Definition | Angles |
|---|---|---|
| Corresponding Angles | Same relative position at each intersection | Equal |
| Alternate Interior Angles | On opposite sides of the transversal, inside the parallel lines | Equal |
| Alternate Exterior Angles | On opposite sides of the transversal, outside the parallel lines | Equal |
| Consecutive Interior Angles | On the same side of the transversal, inside the parallel lines | Sum to 180° |
⚠️ Note: Keep in mind that these properties only hold true when the lines are actually parallel. If they aren’t, these relationships do not apply.
2. Use Proofs to Solidify Understanding
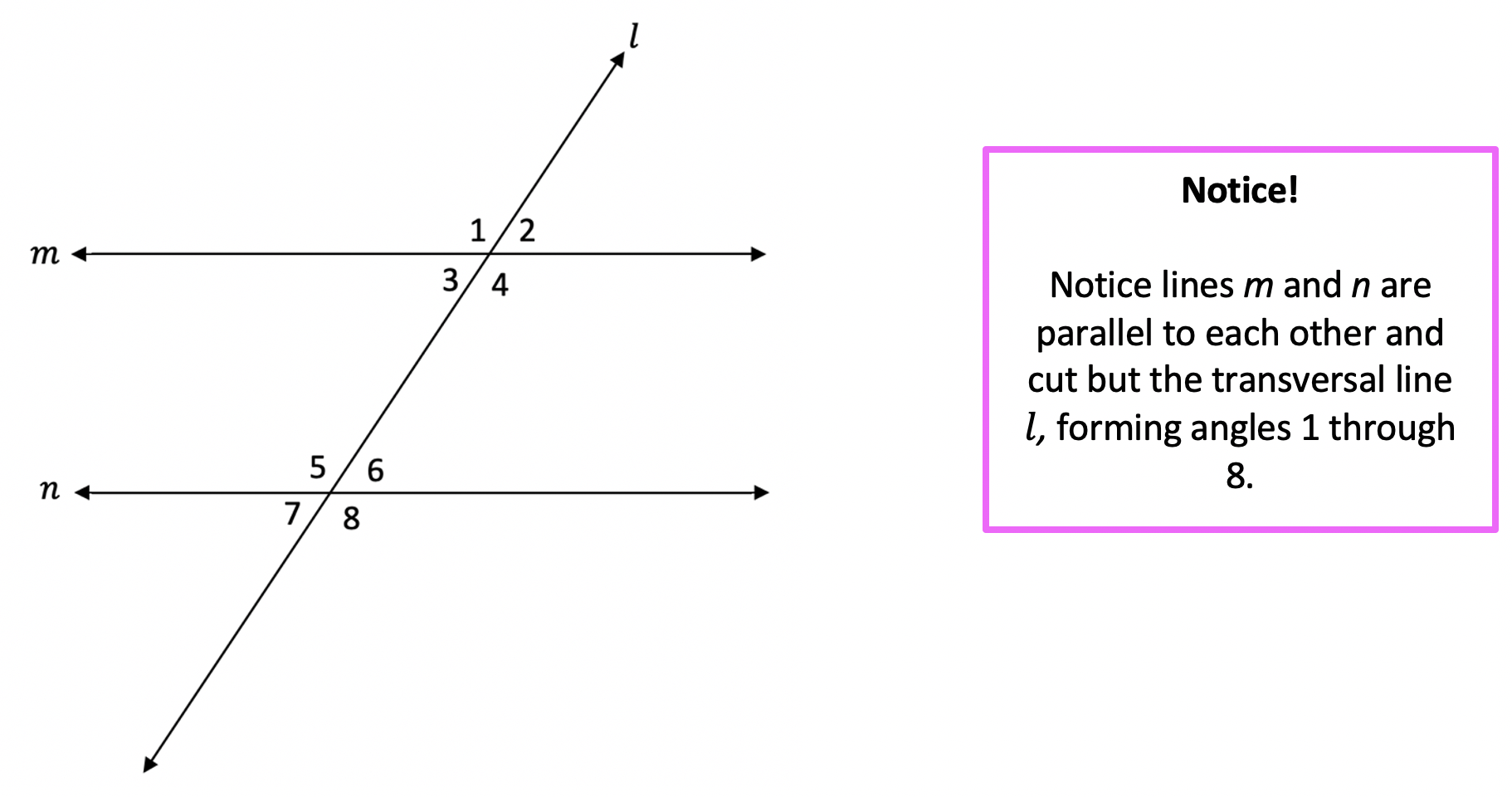
Engaging in geometric proofs can help you:
- Verify the properties of angles created by transversals and parallel lines.
- Apply logical reasoning to understand how these properties derive from axioms.
An example proof for corresponding angles might look like this:
- Assume l || m and t is a transversal.
- Label the angles at the intersection points.
- Use the properties of angles and parallel lines (alternate interior angles, vertical angles, etc.) to prove that the corresponding angles are congruent.
🧠 Note: Proofs in geometry can be quite challenging but are incredibly rewarding for deepening your understanding of the subject.
3. Visualize the Geometry
Visual aids are instrumental in geometry. Here’s how you can benefit from them:
- Create diagrams to visualize how angles relate to each other when parallel lines are cut by a transversal.
- Use color coding to distinguish between different types of angles or lines.
4. Practice with Real-World Examples

Applying geometric concepts to real-life scenarios can make learning more engaging:
- Look for parallel lines and transversals in architecture, like floor tiles or window frames.
- Consider how road markings or railway tracks create angles that correspond to geometric principles.
By doing so, you can:
- Understand the practical implications of geometry.
- Appreciate the beauty of mathematical patterns in everyday life.
5. Solve Problems Systematically

When faced with geometric problems involving parallel lines and transversals:
- Label all points and angles on your diagram.
- Identify known angles and use the relationships between angles to find unknown ones.
- Work step-by-step, always keeping track of your logic to ensure consistency in your problem-solving.
📝 Note: A well-labeled diagram can be your best tool in solving complex geometry problems.
In summary, understanding parallel lines and transversals involves recognizing specific angle relationships, using proofs for verification, visualizing concepts, applying them in practical situations, and solving problems methodically. These approaches not only enhance your understanding of geometry but also enrich your problem-solving skills, providing a solid foundation for further mathematical exploration.
What happens if the lines aren’t parallel?
+
If the lines intersected by a transversal are not parallel, the angles created will not follow the standard rules for corresponding, alternate, or consecutive angles. Instead, you’ll deal with a variety of non-parallel line relationships, such as skew lines or secant lines.
How can I identify parallel lines in a real-world setting?

+
Look for structures or patterns where lines run next to each other indefinitely without intersecting, like railroad tracks, floor tiles, or building facades. Angles formed by these lines with a transversal can give you visual cues to their parallelism.
Why is it important to understand parallel lines and transversals?

+
Understanding these geometric properties is crucial not only for mathematics but also for fields like architecture, engineering, navigation, and even in design where spatial relationships are key to functional and aesthetic outcomes.