5 Ways to Master Parallel Lines & Triangles
Parallel lines and triangles are fundamental concepts in geometry that pave the way for understanding more complex shapes and theorems. Whether you're a student struggling with these concepts or an enthusiast wanting to deepen your knowledge, mastering the rules and relationships of parallel lines and triangles can significantly enhance your geometric problem-solving skills. Here are five detailed ways to gain a robust understanding of these geometric elements.
1. Understand the Properties of Parallel Lines

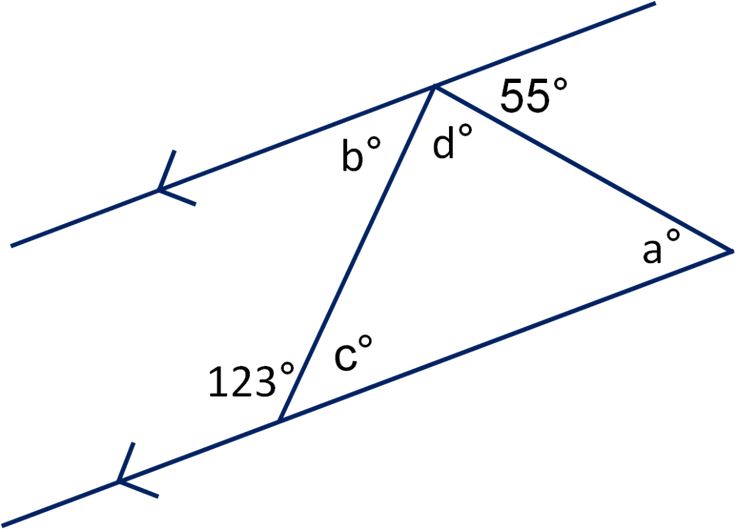
Parallel lines run along the same direction and never intersect. They might seem straightforward, but they interact in profound ways with other geometric figures:
- Transversal Lines: When a transversal cuts across parallel lines, it forms eight angles. Understanding how these angles relate to each other is crucial. Here are the key types:
- Corresponding Angles
- Alternate Interior Angles
- Alternate Exterior Angles
- Same-side (Consecutive) Interior Angles
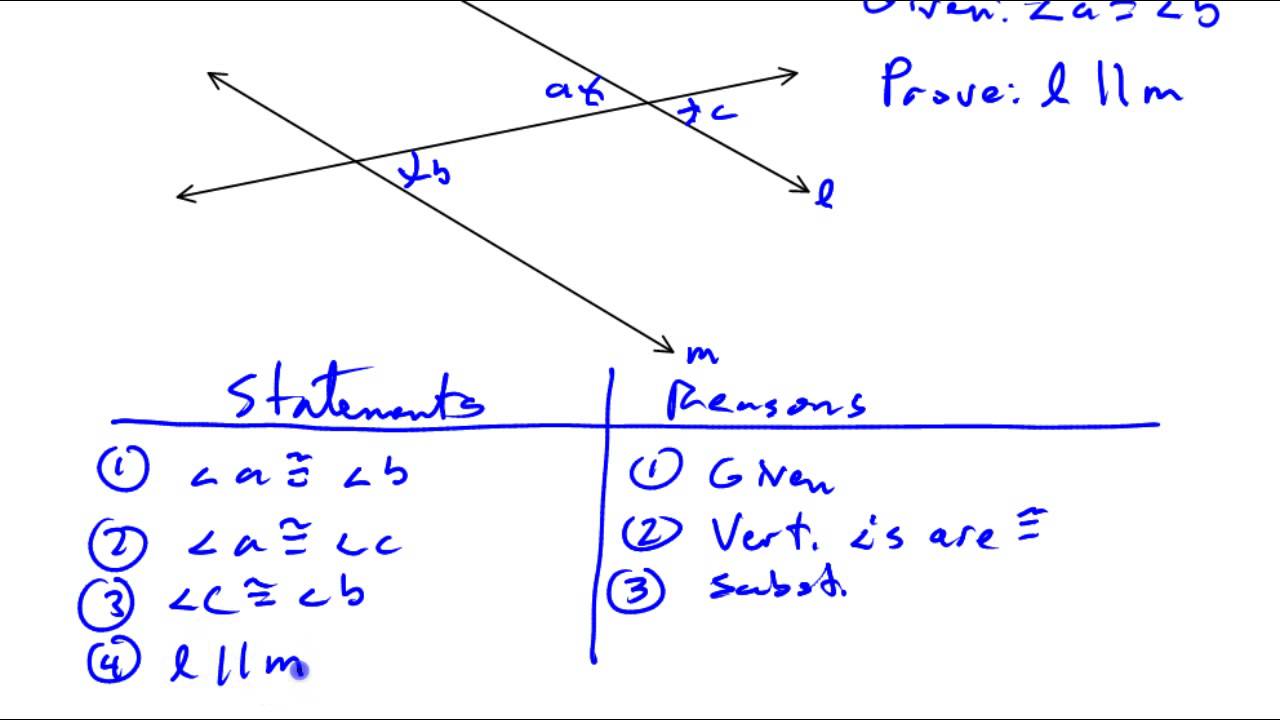
- Key Theorem: If two parallel lines are cut by a transversal, then:
- Corresponding angles are equal.
- Alternate interior angles are equal.
- Same-side interior angles are supplementary.
Mastery in this area involves practicing:
- Recognizing these angles in various geometric problems.
- Proving that lines are parallel given certain conditions.
- Using these properties to solve for missing angles.
📝 Note: Drawing diagrams can help visualize these relationships better. Always label angles clearly for clarity.
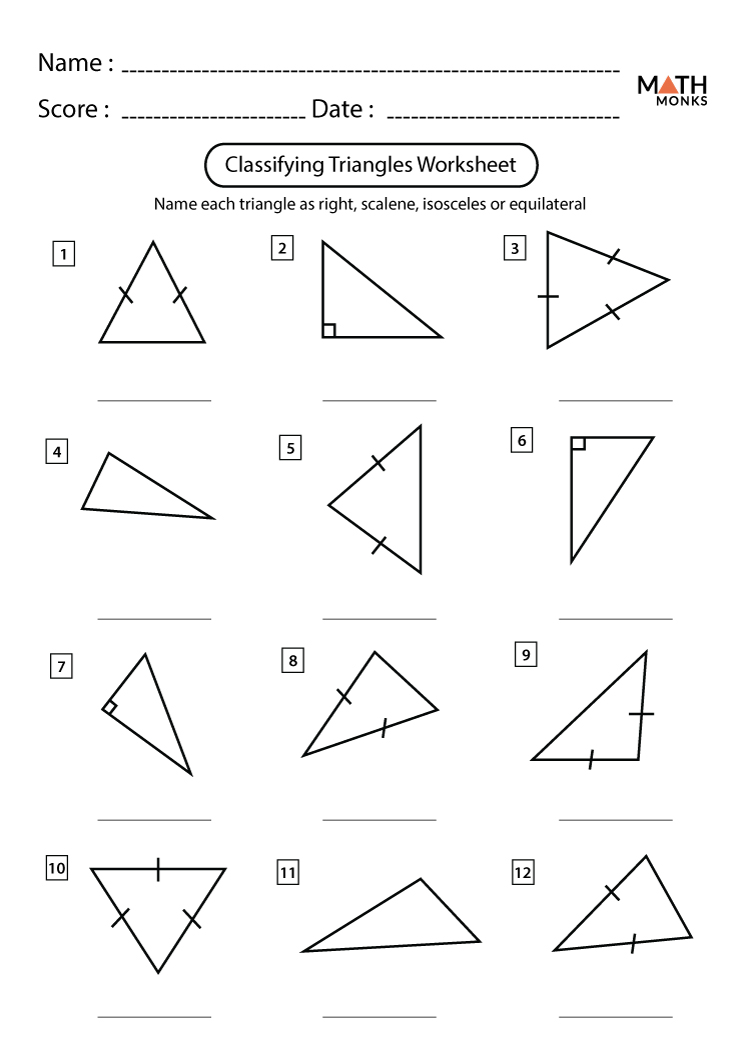
2. Dive into Triangle Classification and Properties

Triangles come in various forms, each with its unique properties:
- By Angles:
- Acute Triangle: All angles are less than 90°.
- Right Triangle: One angle is exactly 90°.
- Obtuse Triangle: One angle is greater than 90°.
- By Sides:
- Equilateral Triangle: All sides are equal.
- Isosceles Triangle: At least two sides are equal.
- Scalene Triangle: No sides are equal.
The sum of angles in any triangle is always 180°. Here's how to apply this knowledge:
- Prove theorems like the Triangle Sum Theorem.
- Use properties to find missing angles or side lengths.
- Understand how triangle properties relate to parallel lines, e.g., in the case of parallel sides creating similar triangles.
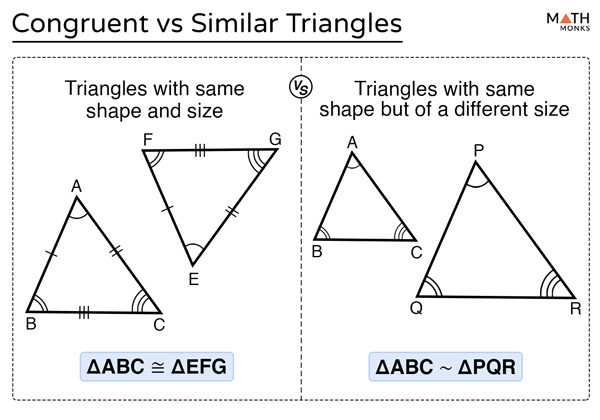
3. Learn to Use Similarity and Congruence
Understanding similarity and congruence is vital for geometric analysis:
- Similarity: Two triangles are similar if their corresponding angles are equal and their corresponding sides are proportional.
- Key Similarity Theorems:
- AA (Angle-Angle)
- SSS (Side-Side-Side)
- SAS (Side-Angle-Side)
- Congruence: Two triangles are congruent if they have the same shape and size, meaning all corresponding sides and angles are equal.
- Key Congruence Postulates:
- SSS
- SAS
- ASA (Angle-Side-Angle)
- AAS (Angle-Angle-Side)
- HL (Hypotenuse-Leg for right triangles)
- Key Congruence Postulates:
These concepts help in:
- Proving that two triangles are identical or similar.
- Calculating ratios and proportions.
- Establishing geometric relationships in more complex figures.
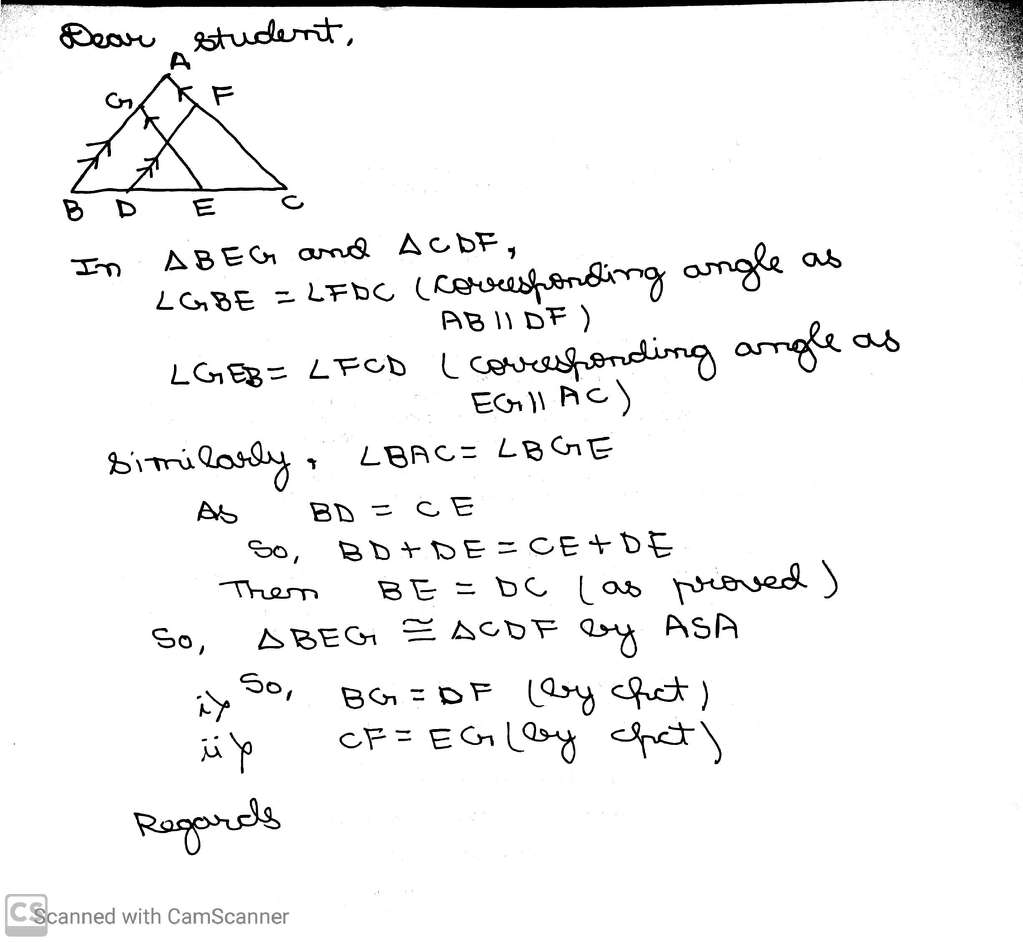
4. Practice with Proofs and Problems
Geometry is largely about proving statements. Here’s how to sharpen your skills:
- Two-Column Proofs: Organize given information, statements, and their reasons.
- Constructing Proofs: Start with what you know and logically deduce conclusions.
- Worksheets and Practice Problems: Regular practice with exercises that require you to apply theorems and postulates.
Practicing proofs involving parallel lines and triangles not only tests your understanding but also reinforces how these shapes interact:
- Using parallel lines to establish congruent angles.
- Proving mid-segments, medians, and altitudes using triangle properties.
📝 Note: Always start with what is given, and remember the logical progression of your proof.
5. Explore Advanced Applications

Mastery goes beyond basic applications:
- Concurrency: Points where lines (like medians or perpendicular bisectors) intersect in triangles.
- Midpoints and Mid-Segments: Using these to prove properties or find lengths.
- Coordinate Geometry: Applying algebraic methods to geometric problems, especially for proving lines parallel or establishing congruency.
These advanced concepts often build on the fundamental relationships you've learned:
- Using coordinate geometry to solve problems involving parallel lines and triangles.
- Understanding how different centers (centroid, incenter, circumcenter) relate to triangle properties.
- Applying these principles to more complex figures and shapes.
The journey to mastering parallel lines and triangles is one of continuous exploration. By diving deep into the properties, theorems, and applications, you not only enhance your geometric understanding but also develop a structured approach to problem-solving, which is invaluable in other mathematical contexts. Embrace these techniques, practice diligently, and watch as geometry transforms from a series of abstract rules into a rich, interconnected tapestry of logic and beauty.
Why are parallel lines important in geometry?
+
Parallel lines provide a foundation for understanding how angles relate to each other through transversals, leading to critical theorems used in both geometry and real-world applications like road design.
What is the difference between similar and congruent triangles?
+
Similar triangles have corresponding angles that are equal and their sides proportional, whereas congruent triangles are identical in shape and size with corresponding parts (angles and sides) exactly equal.
How can understanding triangles and parallel lines help in solving complex geometric problems?

+
These concepts provide a framework for constructing logical arguments and proofs. Understanding how parallel lines and triangles interact allows you to break down complex problems into manageable parts, proving relationships and calculating measurements with confidence.