5 Proven Proofs for Parallel Lines with Transversals

Understanding how lines can relate to each other in Euclidean geometry is fundamental, especially when it comes to parallel lines and transversals. This concept not only forms the basis of many geometric proofs but also has practical applications in fields like architecture, engineering, and more. Here are five proven proofs that illustrate the relationship between parallel lines and transversals.
Corresponding Angles Theorem
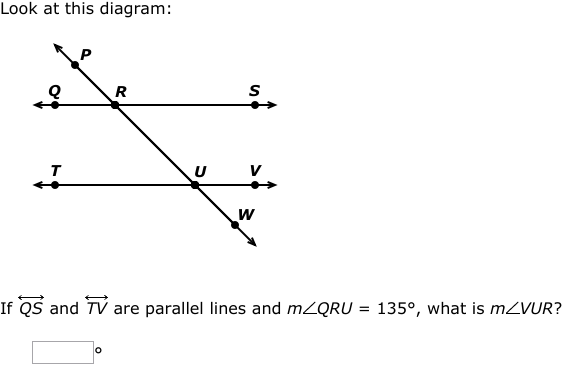
The Corresponding Angles Theorem states that if two parallel lines are cut by a transversal, the pairs of corresponding angles are congruent. Here’s how you can prove this:
- Draw two parallel lines l and m, and a transversal t intersecting both lines.
- Label one of the angles formed where t intersects l as ∠1. This could be either a top-left or top-right angle, but for consistency, let’s say it’s top-right.
- Label the corresponding angle where t intersects m as ∠2. This would be the bottom-right angle.
To prove that ∠1 = ∠2:
- Assume ∠1 = ∠2, which means both angles are equal.
- If they are not equal, then a third line (auxiliary) parallel to l or m would intersect the transversal creating a contradiction with the Euclid’s fifth postulate, which says if a straight line falling on two straight lines makes the interior angles on the same side less than two right angles, the two lines extended indefinitely, will meet on that side.
This proof essentially relies on the fact that if the angles aren’t congruent, then by construction, the lines would meet, contradicting the definition of parallel lines.
Alternate Interior Angles Theorem

The Alternate Interior Angles Theorem tells us that when parallel lines are cut by a transversal, the alternate interior angles are equal.
- Let’s use the same parallel lines l and m with transversal t.
- Label the alternate interior angles formed as ∠3 and ∠4.
- If we assume that ∠3 ≠ ∠4, we could draw a third line parallel to l or m creating a contradiction through the use of corresponding angles.

To see this:
- If ∠3 and ∠4 were not equal, a third line parallel to either l or m would intersect t in a way that would make one of these angles different from the corresponding angles, which contradicts our previous proof.
Consecutive Interior Angles Theorem

The Consecutive Interior Angles Theorem, also known as the Same Side Interior Angles Theorem, states that the sum of consecutive interior angles on the same side of a transversal is 180 degrees when the lines are parallel.
- Again, with l and m as parallel lines, and t as the transversal:
- Label the consecutive interior angles as ∠5 and ∠6.
To prove:
- If we extend line l to intersect a point on line m, we would form a triangle with the transversal.
- Since the sum of the angles in a triangle is 180 degrees, the consecutive interior angles must sum to 180 degrees for the triangle to be well-formed.
Perpendicular Transversal Theorem
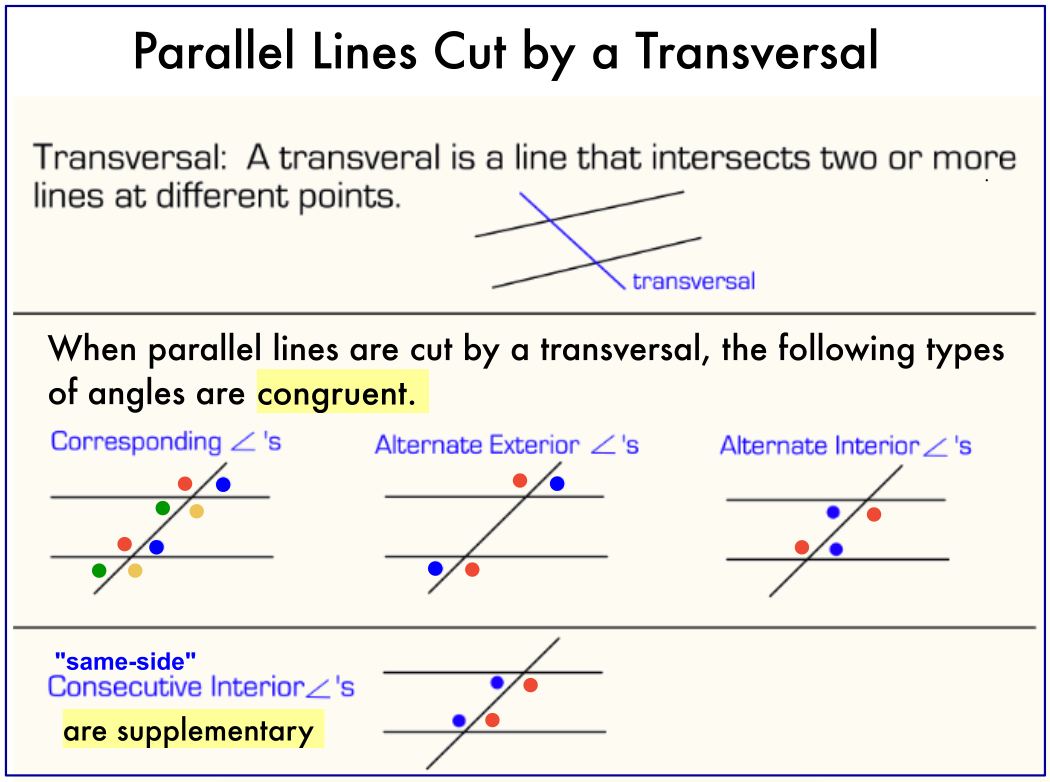
If two parallel lines are cut by a transversal that is perpendicular to one of them, then it is perpendicular to the other as well.
- Consider lines l and m parallel, with transversal t perpendicular to l at point P.
- Label the intersection of t with m as point Q.
To prove:
- Since t is perpendicular to l, ∠PQL = 90°.
- By the Corresponding Angles Theorem, ∠PQL is congruent to ∠LQP. This implies that t forms a right angle with m as well, making it perpendicular.
Transitive Property

This property doesn’t deal directly with angles but uses the fact that if two lines are parallel to the same line, then they are parallel to each other.
- Let lines l and m be parallel, and line n is also parallel to m.
To prove l and n are parallel:
- By definition, if l and m are parallel, the transversal t will form angles that are congruent or supplementary depending on their relative positions.
- Similarly, since m and n are parallel, the same angles will be congruent or supplementary when cut by t.
- Thus, by the transitive property, any transversal intersecting l and n will create angles that match the properties of angles formed by l and m or m and n, establishing that l and n are indeed parallel.
📝 Note: Remember that these proofs depend on the Euclidean postulate, which assumes the existence of parallel lines. In other geometries, such as non-Euclidean geometry, some of these proofs might not hold.
Exploring these proofs provides a solid understanding of the intricate relationships between lines and transversals in plane geometry. Whether you are studying for an exam or exploring mathematical concepts, these theorems and their proofs illustrate not just mathematical principles, but also the logical reasoning that underpins much of geometric thought.
What is a transversal in geometry?

+
A transversal is a line that intersects two or more other lines at different points.
Are these proofs valid in non-Euclidean geometry?

+
In non-Euclidean geometries like spherical or hyperbolic, these proofs might not hold true due to different parallel line definitions. For example, in spherical geometry, there are no parallel lines since any two great circles (analogous to lines on a sphere) will eventually intersect.
How are these proofs useful in real life?

+
They are crucial in fields like architecture for ensuring buildings have perpendicular walls and parallel floors, in engineering for design and construction, and in navigation to understand and predict the path of objects like ships or aircraft.
What is the purpose of learning about parallel lines and transversals?
+
It teaches the foundational skills of logical reasoning, proof construction, and problem-solving, essential for higher mathematics, science, and various practical applications.
Can these proofs be extended to more complex geometric shapes?

+
Yes, these basic principles can be used to understand and prove properties of polygons, polyhedra, and even complex surfaces, as they relate to angles, lines, and planes in higher dimensions.