Parallel Lines Proportional Parts Answers
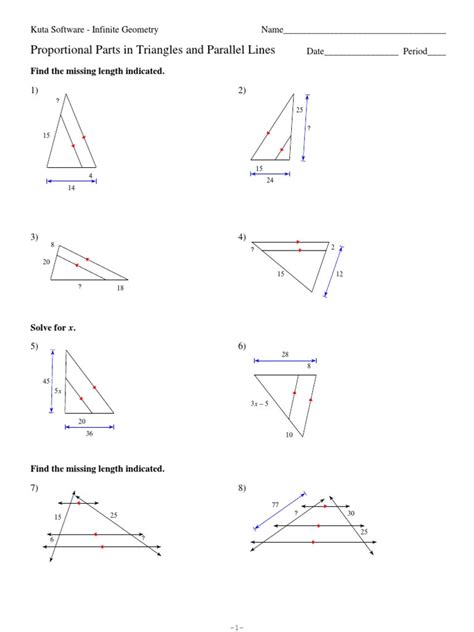
Introduction to Parallel Lines and Proportional Parts

When two lines are cut by a transversal, they create several angles that have special properties. In the case of parallel lines, these angles can be used to determine the similarity of triangles and the proportionality of their sides. The concept of parallel lines and proportional parts is crucial in geometry, as it helps in solving problems related to similar triangles, ratios, and proportions. In this blog post, we will delve into the world of parallel lines, transversals, and proportional parts, and explore their applications in geometry.
Understanding Parallel Lines and Transversals

Parallel lines are lines that lie in the same plane and never intersect, no matter how far they are extended. When a transversal intersects two parallel lines, it creates pairs of corresponding angles, alternate interior angles, and alternate exterior angles. These angles have specific properties that can be used to determine the similarity of triangles and the proportionality of their sides. For instance, corresponding angles are equal, alternate interior angles are equal, and alternate exterior angles are equal.
Proportional Parts Theorem

The Proportional Parts Theorem states that if two lines are cut by a transversal, and the ratios of the lengths of the segments on each line are equal, then the lines are parallel. This theorem can be used to determine whether two lines are parallel or not. For example, if we have two lines, l and m, cut by a transversal, t, and the ratios of the lengths of the segments on each line are equal, i.e., \frac{AB}{BC} = \frac{DE}{EF}, then l and m are parallel.
Similar Triangles and Proportional Parts

Similar triangles have the same shape, but not necessarily the same size. When two triangles are similar, their corresponding sides are proportional. The concept of proportional parts is closely related to similar triangles. If two triangles are similar, and a line intersects the two triangles, then the ratios of the lengths of the segments on each triangle are equal. For instance, if we have two similar triangles, \triangle ABC and \triangle DEF, and a line intersects the two triangles, then the ratios of the lengths of the segments on each triangle are equal, i.e., \frac{AB}{DE} = \frac{BC}{EF}.
Applications of Parallel Lines and Proportional Parts

The concept of parallel lines and proportional parts has numerous applications in geometry, such as: * Solving problems related to similar triangles and ratios * Determining the similarity of triangles * Finding the lengths of segments in triangles * Solving problems related to proportions and ratios
Some examples of problems that can be solved using parallel lines and proportional parts include: * If two lines are cut by a transversal, and the ratios of the lengths of the segments on each line are equal, then the lines are parallel. * If two triangles are similar, and a line intersects the two triangles, then the ratios of the lengths of the segments on each triangle are equal. * If a line intersects two parallel lines, then the ratios of the lengths of the segments on each line are equal.
📝 Note: The concept of parallel lines and proportional parts is essential in geometry, and it has numerous applications in solving problems related to similar triangles, ratios, and proportions.
Table of Parallel Lines and Proportional Parts Properties

The following table summarizes the properties of parallel lines and proportional parts:
| Property | Description |
|---|---|
| Corresponding Angles | Equal |
| Alternate Interior Angles | Equal |
| Alternate Exterior Angles | Equal |
| Proportional Parts Theorem | If two lines are cut by a transversal, and the ratios of the lengths of the segments on each line are equal, then the lines are parallel. |

In summary, parallel lines and proportional parts are essential concepts in geometry, and they have numerous applications in solving problems related to similar triangles, ratios, and proportions. By understanding the properties of parallel lines and proportional parts, we can determine the similarity of triangles, find the lengths of segments in triangles, and solve problems related to proportions and ratios.
To recap, the key points of this blog post are: * Parallel lines are lines that lie in the same plane and never intersect. * The Proportional Parts Theorem states that if two lines are cut by a transversal, and the ratios of the lengths of the segments on each line are equal, then the lines are parallel. * Similar triangles have the same shape, but not necessarily the same size, and their corresponding sides are proportional. * The concept of parallel lines and proportional parts has numerous applications in geometry, such as solving problems related to similar triangles, ratios, and proportions.
What are parallel lines?

+
Parallel lines are lines that lie in the same plane and never intersect, no matter how far they are extended.
What is the Proportional Parts Theorem?

+
The Proportional Parts Theorem states that if two lines are cut by a transversal, and the ratios of the lengths of the segments on each line are equal, then the lines are parallel.
What are similar triangles?

+
Similar triangles have the same shape, but not necessarily the same size, and their corresponding sides are proportional.