5 Proven Ways to Conquer Angles and Parallel Lines
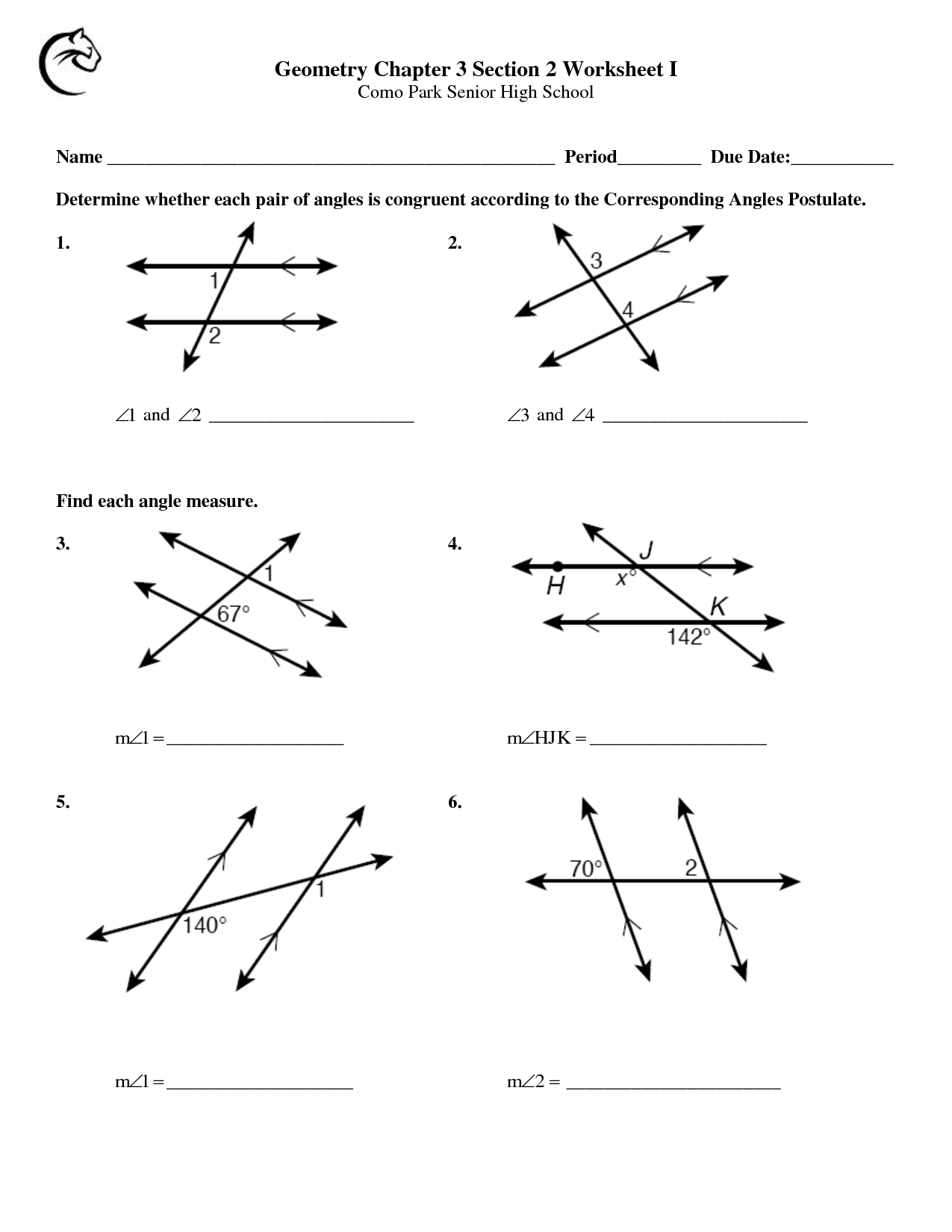
In the world of mathematics, geometry often seems like an insurmountable challenge for many students. However, understanding angles and parallel lines can not only boost your grades but also develop your logical thinking skills. Here's an exhaustive guide to mastering these geometric concepts in ways that will make complex problems appear as simple puzzles.
1. Visualizing Relationships with Diagrams


Geometry is visual by nature. Start by drawing angles and lines accurately on graph paper or using geometric software.
- Identify and mark: Parallel lines, transversal lines, corresponding angles, alternate interior angles, and same-side interior angles.
- Use different colors to highlight relationships for easier identification.
- Label angles with letters or numbers to make it easier to reference when solving problems.
📘 Note: When drawing, ensure your lines are parallel to each other, especially if you're using software, as slight misalignments can mislead your calculations.
2. Mastering Angle Properties

Angles are at the heart of geometric analysis. Here's a quick guide:
- Vertical angles: Always equal when two lines intersect.
- Supplementary angles: Angles that form a straight line, always sum up to 180°.
- Complementary angles: Two angles that add up to 90°.
- Right angles: Always measure 90°.
Understanding these properties will make solving problems involving multiple angles much more intuitive.
3. Leveraging Theorems for Parallel Lines

| Theorem | Definition |
|---|---|
| Alternate Interior Angles Theorem | When two parallel lines are cut by a transversal, alternate interior angles are congruent. |
| Corresponding Angles Postulate | If two parallel lines are cut by a transversal, the pairs of corresponding angles are congruent. |
| Same-Side Interior Angles Theorem | When two parallel lines are cut by a transversal, same-side interior angles are supplementary. |
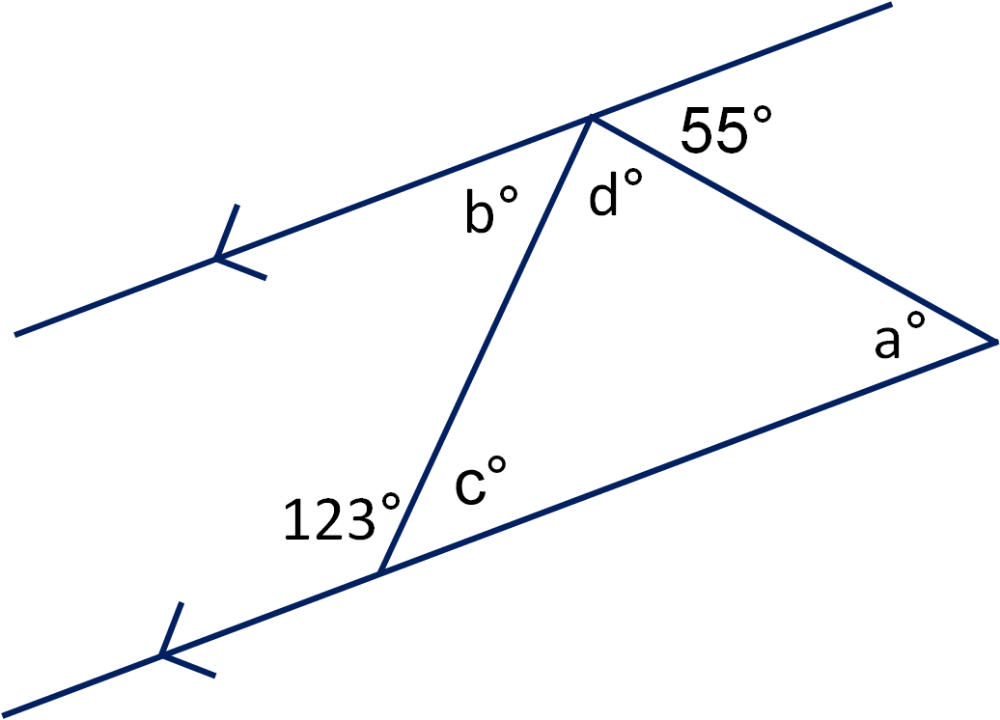
💡 Note: Always check for parallel lines first. If they are parallel, these theorems are directly applicable; if not, the relationships become more complex.
4. Practicing with Proofs

To reinforce your understanding, engage in proving statements or solving geometric proofs:
- Write out steps logically, connecting one conclusion to the next.
- Use diagrams to guide your thought process.
- Read through proofs of others to see different problem-solving approaches.
5. Relating Geometry to Real Life

Make geometry practical:
- Architecture and Design: Look at building plans or urban landscapes where parallel lines and angles are omnipresent.
- Art: Perspective in drawings relies on vanishing points formed by parallel lines.
- Everyday Observations: From bridges to park benches, parallel lines are everywhere. Notice how these structures use angles to maintain stability or aesthetic balance.
In conclusion, by embracing these proven ways to master angles and parallel lines, you're not just solving problems; you're enhancing your spatial awareness and logical reasoning. Applying these principles through visualization, understanding angle properties, leveraging theorems, practicing proofs, and relating them to real-life scenarios will transform geometry from a daunting subject into an engaging challenge. Over time, you'll develop an intuitive sense of how these elements fit together, enabling you to conquer even the trickiest geometric conundrums.
Why is it important to understand angles and parallel lines in geometry?

+
Understanding angles and parallel lines is crucial because they form the basis for many geometric proofs and theorems. This understanding not only helps in solving problems within geometry but also in other fields like physics, engineering, and architecture where spatial relationships are key.
Can these techniques be applied to other areas of mathematics?

+
Yes, these techniques can be applied to other areas like trigonometry, where angles are used to calculate sides of triangles, or in calculus where geometric principles help understand derivatives and integrals in coordinate systems.
What if I can’t visualize angles and lines?

+
Start by practicing simple drawings or using software like GeoGebra. Over time, as you connect geometric theorems with visual representations, your ability to visualize will improve significantly.
How can I remember the angle properties?

+
Mnemonics can help. For example, ‘V’ for Vertical Angles (they’re the same), ’S’ for Supplementary Angles (they make a straight line), ‘C’ for Complementary Angles (they complete a right angle).