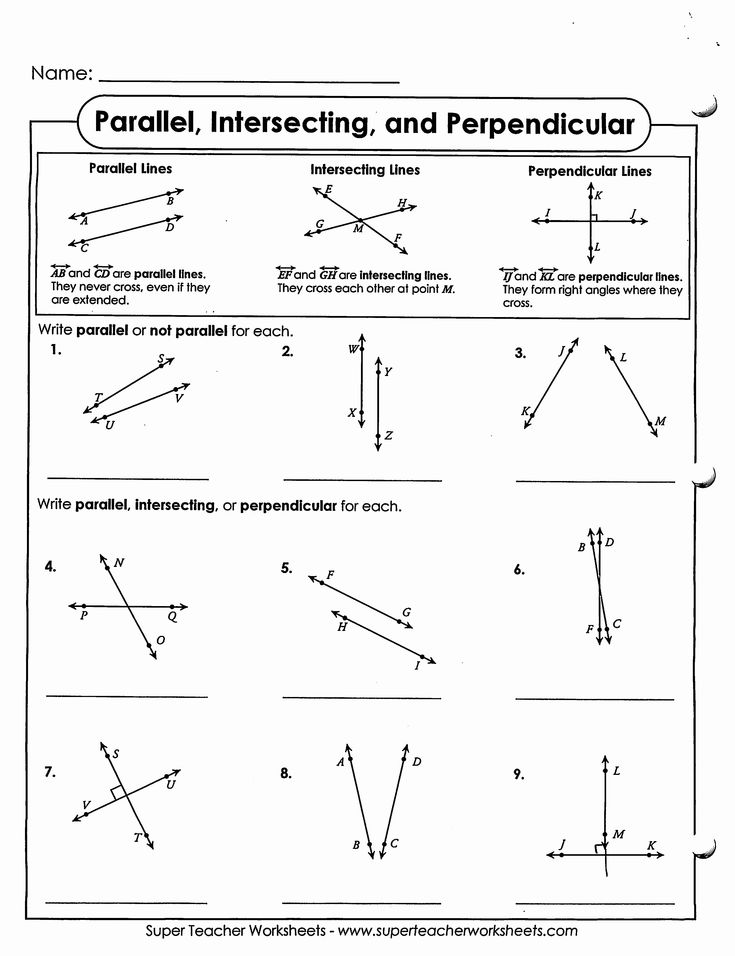
5 Answers to Parallel & Perpendicular Lines Problems

The concept of parallel and perpendicular lines might seem straightforward, but they form the backbone of many geometric principles and are crucial in various real-world applications, from engineering to graphic design. Here, we'll delve into the key aspects of these lines, providing clear explanations, examples, and problem-solving techniques.
Understanding Parallel Lines

Definition: Two lines are parallel if they do not intersect and maintain the same distance between each other throughout their entire length.
- They have the same slope.
- They can be identified by the slope-intercept form of the line equation: y = mx + b, where 'm' is the slope.
Example Problem: Identifying Parallel Lines

Suppose you have two lines:
- Line 1: y = 2x + 3
- Line 2: y = 2x - 5
Are these lines parallel?
Both lines have the same slope, m = 2, indicating that they are indeed parallel. Their y-intercepts differ (3 for Line 1, -5 for Line 2), but this does not affect their parallelism.
💡 Note: Lines with identical slopes are parallel, regardless of their y-intercepts.
Exploring Perpendicular Lines

Definition: Perpendicular lines meet at a right angle (90 degrees).
- Their slopes are negative reciprocals of each other.
- If a line's slope is 'm', its perpendicular line's slope will be -1/m.
Example Problem: Finding a Perpendicular Line
Given a line with the equation y = 4x - 1, find the slope of its perpendicular line.
The slope of the given line is 4, so the slope of the perpendicular line must be -1/4. Therefore, the equation of any line perpendicular to y = 4x - 1 would be in the form y = -1/4x + b, where 'b' is any constant.
Key Relationships and Equations

Slopes of Parallel and Perpendicular Lines

- Parallel lines share identical slopes.
- The product of the slopes of perpendicular lines equals -1.
Here's how these relationships are represented in equations:
| Relationship | Equation |
|---|---|
| Parallel Lines | m1 = m2 |
| Perpendicular Lines | m1 × m2 = -1 |

🔍 Note: Understanding the slopes of perpendicular lines is essential for solving complex geometric problems.
Applications in Real Life

- Civil Engineering: Designing roads and buildings to ensure structural integrity.
- Architecture: Creating right angles for stability and aesthetic purposes.
- Graphic Design: Ensuring parallel and perpendicular alignments for visual appeal.
Strategies for Solving Parallel and Perpendicular Lines Problems

Here are some strategies to efficiently solve these types of problems:
- Identify Slope: Determine the slope from a given line equation or from points on the line.
- Use Reciprocals: To find perpendicular lines, remember to use the negative reciprocal of the slope.
- Graphing: Visual representation can help in understanding line orientation.
When solving, remember:
📝 Note: Always start by determining the slopes when given points or equations. This will guide your approach to parallel and perpendicular line calculations.
Interactive Exercise

Consider this problem for interactive learning:
A line passes through the points (1, 2) and (3, 5). Determine an equation for a line perpendicular to this line that passes through the point (0, -1).
First, calculate the slope of the given line:
m = (5 - 2) / (3 - 1) = 3/2
Since the perpendicular slope is the negative reciprocal:
m_perpendicular = -1 / (3/2) = -2/3
The equation of the perpendicular line is then:
y - (-1) = -2/3(x - 0), simplified to y = -2/3x - 1
This exercise shows the practical application of slopes and their relationships in finding perpendicular lines.
Wrapping Up

Understanding and manipulating parallel and perpendicular lines are key skills in geometry with wide-reaching implications. Whether for design, construction, or problem-solving, these lines' properties guide numerous decisions and calculations. By recognizing how slopes relate between parallel and perpendicular lines, we can simplify and solve complex problems with greater ease. This knowledge not only underpins practical applications but also deepens our understanding of mathematical concepts, enabling us to appreciate the interconnectedness of geometry in both theoretical and practical scenarios.
What does it mean if two lines have the same slope?

+
If two lines share the same slope, they are parallel and will never intersect.
How can I check if two lines are perpendicular?

+
The product of their slopes must be -1 for lines to be perpendicular.
Can you have more than one perpendicular line for a single line?

+
Yes, an infinite number of lines can be perpendicular to a single line as long as they share the same slope’s negative reciprocal.
Why do perpendicular lines have slopes that are negative reciprocals?

+
This relationship ensures that the lines meet at a 90-degree angle, which defines perpendicularity.
Can two lines be both parallel and perpendicular to a third line?

+
Yes, they can be parallel to each other and perpendicular to a third line, but not directly parallel to the third line itself.