5 Simple Steps for Solving Integer Operations

Mathematics, often seen as a challenging subject, has a beauty in its simplicity and exactness. Integer operations, while foundational, can still pose difficulties for students if not approached systematically. By mastering these basic operations—addition, subtraction, multiplication, and division—you can tackle more complex problems in mathematics with ease. Here, we will delve into a practical, step-by-step guide on how to solve integer operations effectively, making what might seem intricate much more accessible.
Understanding Integers

Before diving into the operations, it’s crucial to understand what integers are. Integers include all whole numbers, both positive and negative, along with zero. Here are some key points:
- Integers are represented on a number line where positive integers are to the right of zero and negative integers to the left.
- Zero itself is considered an integer.
- Fractions and decimals are not integers.
Addition of Integers

Adding integers might seem simple, but the sign of the numbers changes the game:
- Adding two integers with the same sign: Add their absolute values, then keep the same sign. For example, (-4) + (-7) = -11.
- Adding two integers with different signs: Subtract their absolute values, and the sign of the result follows the number with the larger absolute value. For example, (-8) + 5 = -3.
🔍 Note: The absolute value of a number is its distance from zero on the number line, disregarding its sign.
Subtraction of Integers

Subtracting integers can be transformed into addition by changing the sign of the subtrahend:
- Turn subtraction into addition: (-7) - (-4) becomes (-7) + (+4) = -3.
- Keep the sign for subtraction: If you subtract a positive number from a negative number, you move further left on the number line, making the result more negative.
Multiplication and Division of Integers
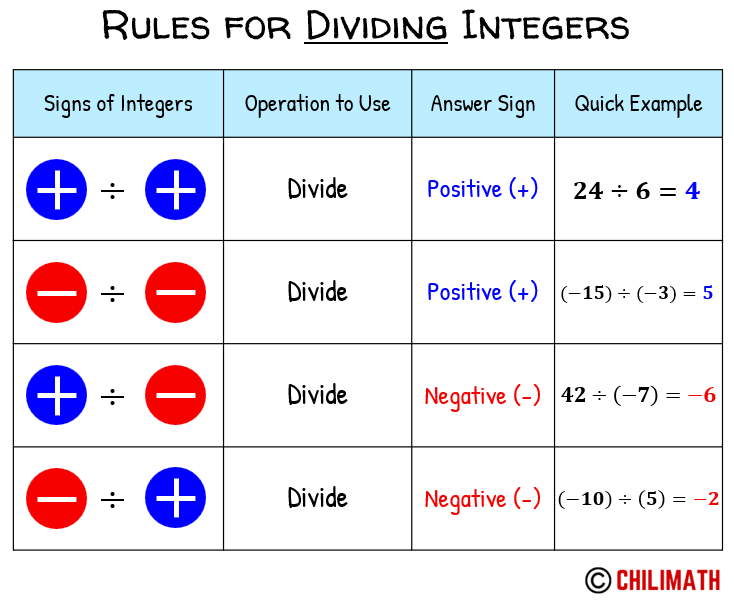
The rules for multiplying or dividing integers depend on their signs:
- Same signs: When you multiply or divide two integers with the same sign, the result is positive.
- Different signs: If the signs are different, the result is negative.
| Operation | Sign of Numbers | Result Sign |
|---|---|---|
| Multiplication or Division | Positive * Positive or Negative * Negative | Positive |
| Multiplication or Division | Positive * Negative or Negative * Positive | Negative |

Solving Integer Equations

After understanding the operations, solving integer equations becomes a logical exercise:
- Isolate the variable on one side of the equation.
- Use the rules of operation to simplify the equation step by step.
- Remember to do the same operation to both sides of the equation to maintain balance.
For instance, solving the equation x + 7 = 2 involves subtracting 7 from both sides to isolate x:
x + 7 - 7 = 2 - 7
x = -5
Practical Applications of Integer Operations

Understanding integer operations isn't just about solving equations; it's about applying these principles to real-world scenarios:
- Finance: Keeping track of debit (negative integers) and credit (positive integers) in an account.
- Temperature: Recording temperatures above and below freezing.
- Elevation: Dealing with sea levels and heights.
🌡 Note: Negative numbers are often used to indicate temperatures below freezing or levels below sea level.
Tips for Mastery

Here are some strategies to ensure you become proficient with integer operations:
- Practice regularly: Use flashcards or online tools to solidify your understanding.
- Visual aids: Draw number lines or use blocks to physically represent positive and negative numbers.
- Apply concepts: Solve real-world problems involving integers to see the practicality of these operations.
🔤 Note: Understanding negative numbers as "the opposite of" can simplify many operations.
Mastering integer operations is not just about recalling the rules; it's about developing an intuitive understanding of numbers. Through consistent practice, visual learning, and real-world application, you can turn these operations from a daunting task into a clear, logical process. The foundation of arithmetic and beyond lies in these basic principles, making the effort to understand them a worthwhile investment in your mathematical education.
What is the sign of an integer operation result when dealing with different signs?

+
When multiplying or dividing two integers with different signs, the result will always be negative.
Why do we add or subtract before we multiply or divide in an equation?

+
Order of operations dictates that addition and subtraction are performed after multiplication and division to ensure the equation’s balance.
How can I visualize integer operations?

+
Using a number line can help visualize movement in positive or negative directions. Additionally, employing colored blocks or counters where positive integers are one color and negative integers are another can be visually instructive.
What are some common mistakes when dealing with integer operations?

+
Common mistakes include: forgetting the sign rule in multiplication or division, treating subtraction as addition without sign change, and not following the order of operations.


