5 Quick Steps for Fraction Operations Mastery

Mastering fraction operations is a fundamental skill in mathematics, essential for students from elementary to high school levels. Understanding how to work with fractions not only aids in solving complex problems but also improves number sense and prepares learners for algebra and beyond. In this comprehensive guide, we'll explore five quick steps to master fraction operations, including addition, subtraction, multiplication, and division, along with practical examples to ensure you or your students grasp these concepts with ease.
Step 1: Understanding Fraction Basics


Before diving into operations, it’s critical to ensure that fractions are understood at their core. Fractions consist of a numerator (the top number) and a denominator (the bottom number). Here’s what you need to know:
- Proper Fractions: The numerator is smaller than the denominator, like (\frac{2}{3}).
- Improper Fractions: The numerator is equal to or larger than the denominator, like (\frac{7}{3}).
- Mixed Numbers: A whole number combined with a fraction, such as (1 \frac{1}{4}), where the whole number is 1 and the fraction part is (\frac{1}{4}).
- Equivalent Fractions: Fractions representing the same value, like (\frac{2}{4}), (\frac{1}{2}), and (\frac{3}{6}).
🌟 Note: Recognizing the type of fraction you’re dealing with is the first step towards effective fraction operations.
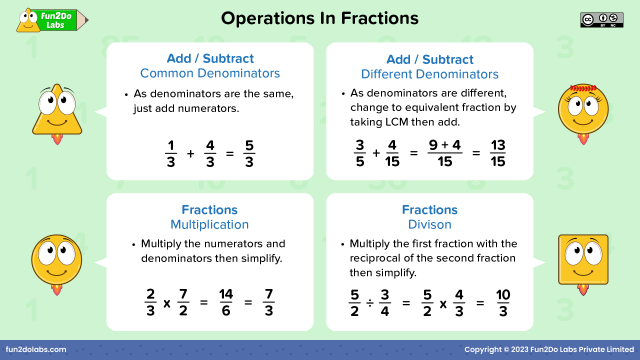
Step 2: Adding and Subtracting Fractions


Adding and subtracting fractions involves two key rules:
- If denominators are the same, add or subtract the numerators directly, keeping the denominator unchanged. For example, (\frac{1}{4} + \frac{2}{4} = \frac{3}{4}).
- If denominators differ, you must find a common denominator. Here’s how:
- Identify the least common denominator (LCD).
- Convert each fraction to an equivalent fraction with the LCD.
- Add or subtract the numerators, then simplify if possible.
Example:
To add (\frac{1}{3} + \frac{1}{6}):
- The LCD is 6.
- Convert (\frac{1}{3}) to (\frac{2}{6}).
- Add: (\frac{2}{6} + \frac{1}{6} = \frac{3}{6}).
- Simplify: (\frac{3}{6} = \frac{1}{2}).
🔍 Note: The least common denominator is crucial for efficient operations; it ensures the fractions are compatible for addition or subtraction.
Step 3: Multiplying Fractions


Multiplying fractions is more straightforward:
- Multiply the numerators together to get the new numerator.
- Multiply the denominators to get the new denominator.
- Simplify if possible.
Example:
For (\frac{2}{3} \times \frac{4}{5}):
- New numerator: (2 \times 4 = 8)
- New denominator: (3 \times 5 = 15)
- Result: (\frac{8}{15}) (which cannot be simplified further)
Multiplying mixed numbers involves converting them to improper fractions first.
💡 Note: When multiplying fractions, the result does not need to have a common denominator, simplifying the process.
Step 4: Dividing Fractions


Dividing fractions involves a special technique:
- Keep the first fraction as is.
- Flip the second fraction (take its reciprocal).
- Change the division sign to multiplication, and then follow the steps for multiplying fractions.
Example:
To divide (\frac{3}{4}) by (\frac{2}{3}):
- Keep (\frac{3}{4}) as is.
- Flip (\frac{2}{3}) to (\frac{3}{2}).
- Multiply: (\frac{3}{4} \times \frac{3}{2} = \frac{9}{8}) (which can be simplified to (1 \frac{1}{8}))
📝 Note: Dividing by a fraction is equivalent to multiplying by its reciprocal, a key concept in fractional operations.
Step 5: Practice and Application

| Operation | Example Problem | Solution |
|---|---|---|
| Addition | (\frac{5}{8} + \frac{3}{4}) | Find the LCD (8), convert (\frac{3}{4}) to (\frac{6}{8}), add the numerators: (\frac{5}{8} + \frac{6}{8} = \frac{11}{8}) or (1 \frac{3}{8}) |
| Subtraction | (\frac{7}{10} - \frac{1}{2}) | Find the LCD (10), convert (\frac{1}{2}) to (\frac{5}{10}), subtract the numerators: (\frac{7}{10} - \frac{5}{10} = \frac{2}{10}) or (\frac{1}{5}) |
| Multiplication | (\frac{1}{4} \times \frac{3}{5}) | Multiply numerators: (1 \times 3 = 3). Multiply denominators: (4 \times 5 = 20). Result: (\frac{3}{20}) |
| Division | (\frac{5}{6} \div \frac{2}{3}) | Flip the second fraction: (\frac{3}{2}). Multiply: (\frac{5}{6} \times \frac{3}{2} = \frac{15}{12}). Simplify: (\frac{5}{4}) or (1 \frac{1}{4}) |
Practice is key to mastering any mathematical concept, and fraction operations are no exception. Here are a few tips to enhance practice:
- Use visual aids like pie charts or fraction strips to represent fractions visually.
- Solve problems daily, starting with simpler ones and gradually increasing complexity.
- Include real-life problems where fractions are naturally used, like measuring ingredients or dividing a pizza.
- Engage in online fraction games or use math apps that provide interactive fraction practice.
To wrap up, understanding and mastering fraction operations can significantly enhance your mathematical proficiency, paving the way for algebra, calculus, and beyond. This guide has laid out a structured path through understanding, adding, subtracting, multiplying, and dividing fractions. With these steps and consistent practice, you’ll find that fractions become less daunting, opening up a world of mathematical exploration.
What is a fraction?
+
A fraction represents a part of a whole or a ratio between two numbers. It consists of a numerator (the top number) and a denominator (the bottom number). For example, (\frac{1}{2}) means one part of two equal parts.
Why do we need to find a common denominator?

+
Finding a common denominator is necessary when adding or subtracting fractions because it ensures that the fractions refer to the same unit or size of parts. This commonality allows for direct comparison and arithmetic operations between them.
Can you divide by a fraction?

+
Yes, you can divide by a fraction. You do this by multiplying by its reciprocal, which essentially inverts the fraction you are dividing by. So, dividing (\frac{a}{b}) by (\frac{c}{d}) is the same as multiplying (\frac{a}{b}) by (\frac{d}{c}).
How do I practice fractions?

+
Practicing fractions can be done through worksheets, online games, using fraction manipulatives, or by solving real-life problems. Consistency and varied practice methods enhance understanding.
What is the importance of simplifying fractions?

+
Simplifying fractions reduces them to their smallest, most reduced form, making them easier to work with and understand. It also helps in making calculations simpler and quicker, especially when dealing with larger numbers.