Polynomial Operations Worksheet Answers: Master Polynomials Easily

Polynomials, though often challenging, form the backbone of algebra and are pivotal in various fields like engineering, finance, computer science, and physics. Mastering polynomials not only enhances your mathematical skills but also equips you with tools to solve real-world problems. In this comprehensive blog post, we'll delve into polynomial operations, providing step-by-step guidance through problems and solutions to help you master this topic with ease.
Understanding Polynomials

Before we jump into operations, let’s ensure we have a solid grasp on what polynomials are:
- A polynomial is an expression consisting of variables and coefficients, involving only the operations of addition, subtraction, multiplication, and non-negative integer exponents of variables.
- Examples include (3x^2 + 2x + 1), (4a^3 - 2ab^2 + 6a), or even constants like (7).
Each part of the polynomial separated by addition or subtraction is called a term, and these terms can be classified as monomials, binomials, or trinomials based on the number of terms.
Polynomial Addition and Subtraction

Adding or subtracting polynomials involves combining like terms:
- Like terms are terms with the same variable raised to the same power.
| Example | Operation | Result |
|---|---|---|
| (3x^2 + 4x - 7) + (2x^2 - 5x + 3) | Add | 5x^2 - x - 4 |
| (6x^3 - x + 1) - (2x^3 + 4x - 5) | Subtract | 4x^3 - 5x + 6 |

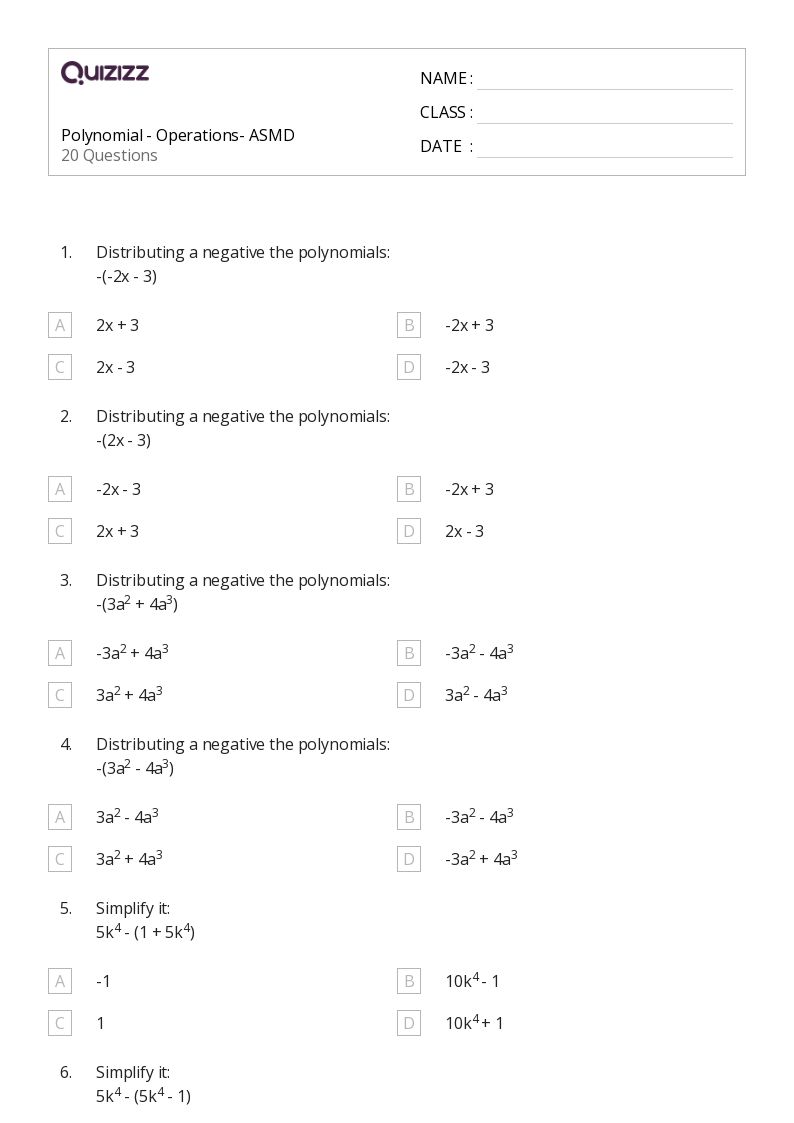
📝 Note: Always ensure to distribute the negative sign when subtracting polynomials.
Polynomial Multiplication

Multiplying polynomials involves using the distributive property (each term in one polynomial is multiplied by every term in the other):
- Use the FOIL method for binomials.
- For larger polynomials, distribute each term from one polynomial to every term of the other.
| Polynomials | Result |
|---|---|
| (x+2)(x-3) | x^2 - x - 6 |
| (2x^2 - 1)(3x - 2) | 6x^3 - 5x^2 - 3x + 2 |
Here, the FOIL method expands (First, Outer, Inner, Last), while for larger polynomials, you distribute each term individually:
- (2x^2)(3x) + (2x^2)(-2) + (-1)(3x) + (-1)(-2)
Polynomial Division

Polynomial division can be approached in two primary ways:
- Long Division: Similar to arithmetic division where you:
- Divide the leading term of the dividend by the leading term of the divisor.
- Multiply this result by the divisor.
- Subtract this product from the original dividend.
- Repeat until the degree of the remainder is less than the degree of the divisor or zero.
- Synthetic Division: A simplified method for dividing by binomials of the form x - c.
Example of Long Division

Divide 2x^4 + 3x^3 - 16x^2 + 17x - 6 by 2x^2 - x + 1
- Start by dividing 2x^4 by 2x^2 to get x^2 as the first term of the quotient.
- Multiply x^2 by 2x^2 - x + 1 to get 2x^4 - x^3 + x^2.
- Subtract this from the original polynomial to get 4x^3 - 17x^2 + 17x - 6.
- Repeat the process until the remainder is of a lower degree or zero:
The result would be x^2 + 2x - 9 + \frac{12x - 3}{2x^2 - x + 1}
📝 Note: The remainder in polynomial division often represents the incompleteness of the polynomial fit to the function.
Example of Synthetic Division

Divide (x^3 + 4x^2 + x - 6) by (x - 2)
- Set up your synthetic division with 2 as the root (since (x - 2 = 0) when (x = 2)).
- Bring down the leading coefficient, multiply by 2, add to the next coefficient, repeat.
The result would be (x^2 + 6x + 13 + \frac{20}{x-2}).
Factoring Polynomials
Factoring involves breaking down polynomials into products of factors, which can reveal useful properties about the polynomial:
- Use the greatest common factor (GCF) to factor out common terms.
- Factor binomials using special products or difference of squares.
- Group terms or use polynomial identities for complex factorization.
| Polynomial | Factored Form |
|---|---|
| x^2 - 9 | (x - 3)(x + 3) |
| x^2 - 5x + 6 | (x - 2)(x - 3) |
📝 Note: Factoring can significantly simplify solving equations or identifying roots.
Solving Polynomial Equations

Once you’ve factored a polynomial, solving it for its roots involves setting each factor to zero. Here’s how:
- Factor the polynomial completely.
- Set each factor equal to zero and solve for (x).
Consider the polynomial (x^3 - 3x^2 - 4x + 12):
- Factor to ((x - 2)(x - 3)(x + 2)).
- Set each factor to zero: (x - 2 = 0), (x - 3 = 0), (x + 2 = 0).
- The roots are (x = 2), (x = 3), and (x = -2).
In this journey through polynomial operations, we’ve covered:
- The basic structure and terminology of polynomials.
- Techniques for adding, subtracting, multiplying, and dividing polynomials.
- Approaches to factoring polynomials.
- Methods for solving polynomial equations.
To master polynomials, practice is crucial. Try to work through various problems, apply these techniques, and understand the underlying principles. Whether for academic excellence, competitive exams, or real-world problem solving, polynomial operations are indispensable. Remember, the elegance of mathematics often lies in its simplicity; even the most complex polynomial can be unraveled with patience and understanding.
What are the degrees of a polynomial?

+
The degree of a polynomial is the highest power of the variable in the polynomial. For example, in (2x^4 + 3x^2 - 5), the degree is 4 because the highest power of (x) is 4.
Can polynomials have non-integer exponents?

+
By definition, polynomials only involve variables with non-negative integer exponents. Expressions with non-integer exponents are part of more general algebraic expressions.
How do I know when to use synthetic division or long division?

+
Use synthetic division when dividing by a linear factor (polynomial of degree 1 like (x - c)). Long division is used for more general polynomial division or when the divisor is not in the form (x - c).