5 Ways to Master Operations With Fractions
Understanding Fractions: The Foundation of Mastering Operations

Fractions are a fundamental concept in mathematics, representing a part of a whole. They are used to describe proportions, ratios, and decimals, making them a crucial aspect of various mathematical operations. Mastering operations with fractions requires a solid understanding of their basics, which includes addition, subtraction, multiplication, and division. In this article, we will explore five ways to master operations with fractions, covering the essential concepts, rules, and tips to help you become proficient.
1. Simplifying Fractions: The Key to Efficient Operations

Simplifying fractions is the process of reducing a fraction to its lowest terms. This step is essential before performing any operation with fractions. To simplify a fraction, you need to find the greatest common divisor (GCD) of the numerator and denominator and divide both by the GCD.
Why Simplify Fractions?
- Simplifying fractions reduces the complexity of operations
- It helps to avoid errors in calculations
- Simplified fractions make it easier to compare and order fractions
Example:
Simplify the fraction 6⁄8
- Find the GCD of 6 and 8, which is 2
- Divide both the numerator and denominator by 2: 6 ÷ 2 = 3, 8 ÷ 2 = 4
- The simplified fraction is 3⁄4
💡 Note: Always simplify fractions before performing operations to ensure accuracy and efficiency.
2. Adding and Subtracting Fractions: Finding a Common Denominator
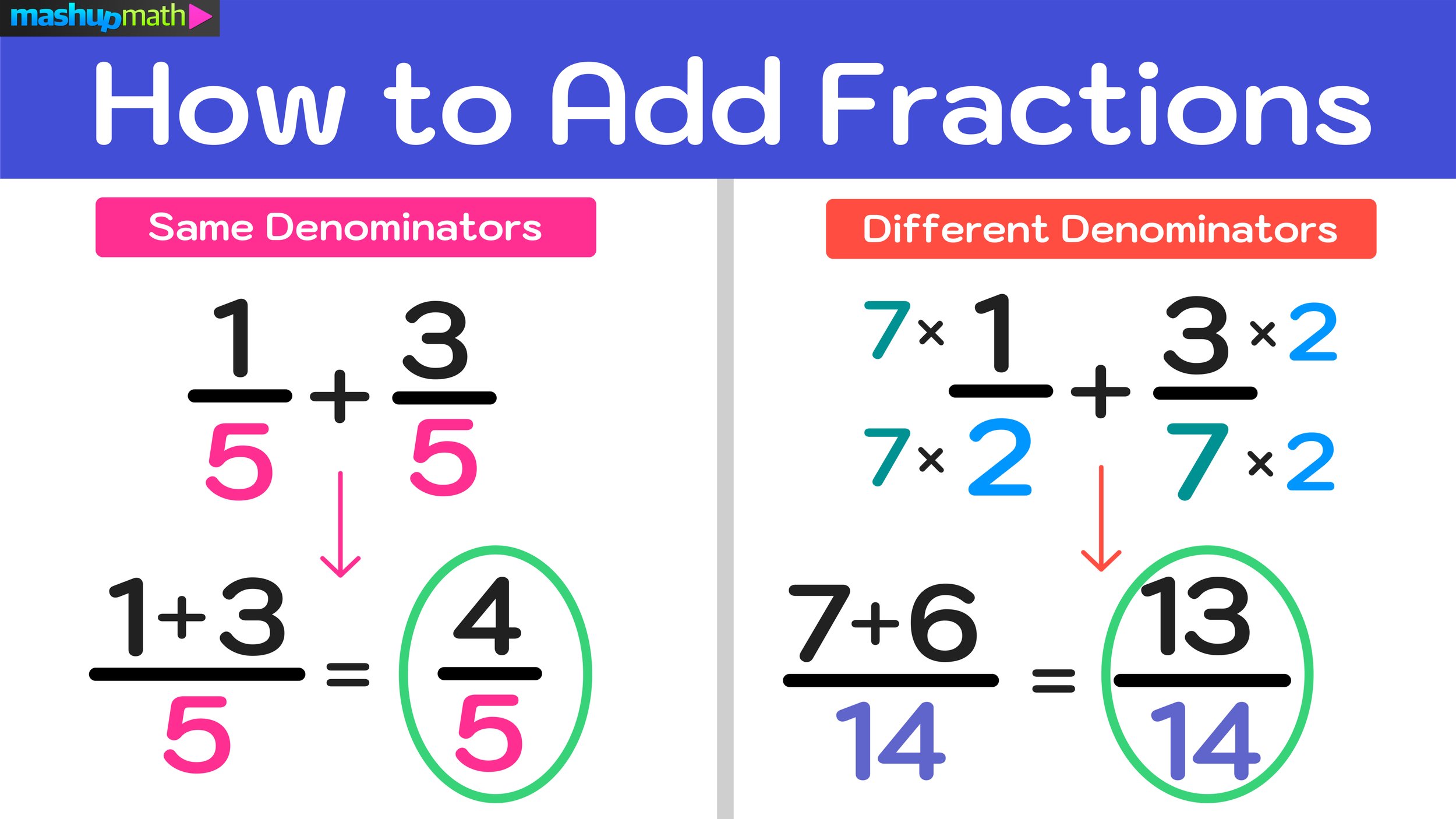
Adding and subtracting fractions require finding a common denominator, which is the least common multiple (LCM) of the denominators. Once you have the common denominator, you can add or subtract the numerators.
Rules for Adding and Subtracting Fractions:
- Find the LCM of the denominators
- Convert each fraction to have the LCM as the denominator
- Add or subtract the numerators
- Simplify the resulting fraction
Example:
Add 1⁄4 and 1⁄6
- Find the LCM of 4 and 6, which is 12
- Convert each fraction: 1⁄4 = 3⁄12, 1⁄6 = 2⁄12
- Add the numerators: 3 + 2 = 5
- The result is 5⁄12
📝 Note: When adding or subtracting fractions, make sure to find the LCM of the denominators to ensure accurate results.
3. Multiplying Fractions: The Rule of Multiply and Simplify

Multiplying fractions involves multiplying the numerators and multiplying the denominators. The resulting fraction can then be simplified.
Rules for Multiplying Fractions:
- Multiply the numerators
- Multiply the denominators
- Simplify the resulting fraction
Example:
Multiply 1⁄2 and 3⁄4
- Multiply the numerators: 1 × 3 = 3
- Multiply the denominators: 2 × 4 = 8
- The result is 3⁄8
💡 Note: When multiplying fractions, remember to multiply the numerators and denominators separately before simplifying the resulting fraction.
4. Dividing Fractions: Inverting and Multiplying

Dividing fractions involves inverting the second fraction (i.e., flipping the numerator and denominator) and then multiplying.
Rules for Dividing Fractions:
- Invert the second fraction
- Multiply the numerators
- Multiply the denominators
- Simplify the resulting fraction
Example:
Divide 1⁄2 by 3⁄4
- Invert the second fraction: 3⁄4 becomes 4⁄3
- Multiply the numerators: 1 × 4 = 4
- Multiply the denominators: 2 × 3 = 6
- The result is 4⁄6, which simplifies to 2⁄3
📝 Note: When dividing fractions, remember to invert the second fraction and then multiply to get the correct result.
5. Practicing Operations with Fractions: Building Proficiency

Mastering operations with fractions requires practice. Start with simple problems and gradually move on to more complex ones. You can use online resources, worksheets, or math games to build your proficiency.
Tips for Practicing Operations with Fractions:
- Start with simple problems and gradually increase the difficulty level
- Use visual aids like fraction strips or circles to help you understand the concepts
- Practice regularly to build your confidence and accuracy
- Use real-world examples to make fraction operations more meaningful
| Operation | Example | Rule |
|---|---|---|
| Addition | 1/4 + 1/6 | Find the LCM, add numerators, and simplify |
| Subtraction | 1/4 - 1/6 | Find the LCM, subtract numerators, and simplify |
| Multiplication | 1/2 × 3/4 | Multiply numerators, multiply denominators, and simplify |
| Division | 1/2 ÷ 3/4 | Invert second fraction, multiply, and simplify |

By following these five ways to master operations with fractions, you will become proficient in performing calculations with fractions. Remember to simplify fractions, find common denominators, multiply and simplify, invert and multiply, and practice regularly to build your skills.
In summary, mastering operations with fractions requires a solid understanding of the basics, including simplifying fractions, finding common denominators, multiplying and dividing fractions. By practicing regularly and using visual aids, you can build your proficiency and become confident in performing calculations with fractions.
What is the importance of simplifying fractions?

+
Simplifying fractions is essential to reduce the complexity of operations, avoid errors in calculations, and make it easier to compare and order fractions.
How do I add and subtract fractions?

+
To add and subtract fractions, find the least common multiple (LCM) of the denominators, convert each fraction to have the LCM as the denominator, add or subtract the numerators, and simplify the resulting fraction.
What is the rule for multiplying fractions?

+
The rule for multiplying fractions is to multiply the numerators, multiply the denominators, and simplify the resulting fraction.
Related Terms:
- Operations with fractions worksheet pdf
- Operations with Fractions Worksheet Kuta