5 Tips for Mastering Negative Exponents Quickly

Mathematics can often seem like an arcane language filled with symbols and rules that can be difficult to understand, especially when you dive into exponents. While mastering exponents might seem daunting, the field of negative exponents holds a special kind of magic. Negative exponents are not just another algebraic concept; they are a gateway to understanding division and fractions in a whole new light. In this detailed guide, we'll explore five actionable tips that can help you master negative exponents quickly and with confidence.
1. Understand the Definition of Negative Exponents

Before you can conquer any aspect of exponents, you must first grasp what they are and how they work. A negative exponent implies a reciprocal operation:
- Negative Exponent: For any non-zero number a and any integer n, a^{-n} = \frac{1}{a^n}.
Here's an example to illustrate:
If you have 5^{-2}, rather than an intimidating operation, you should see it as:
5^{-2} = \frac{1}{5^2} = \frac{1}{25}
💡 Note: Remember, any number raised to the power of zero equals 1 (a^0 = 1), even when dealing with negative exponents.
2. Practice with Flashcards and Apps

Utilizing modern educational tools can transform your learning experience. Flashcards are a tried and true method for memorizing formulas and rules. Use an app or create your own flashcards:
- Write a^{-n} = \frac{1}{a^n} on one side.
- On the other, provide an example like 2^{-3} = ?

Apps like Quizlet or Khan Academy can offer interactive practice sessions tailored to negative exponents, adjusting the difficulty as you progress.
🚫 Note: Avoid using apps that only teach rules without providing sufficient practice. The key to mastering negative exponents is consistent application of the rule.
3. Use Real-life Examples and Visualizations
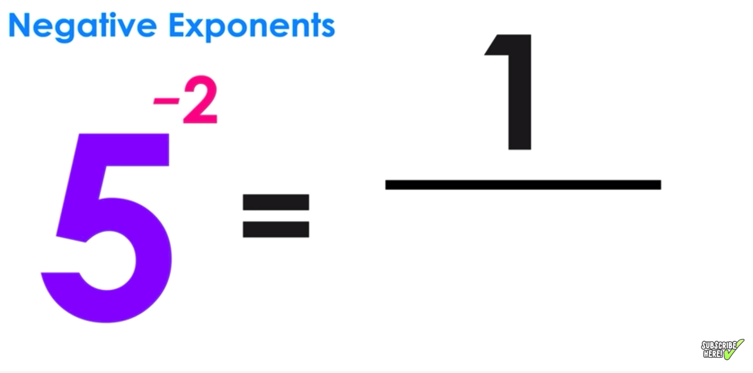
Mathematics becomes much clearer when grounded in real-life scenarios. Here's a visualization you might find helpful:
| Negative Exponent | Real-life Example |
|---|---|
| 10^{-1} | 1 cm = 0.1 meters or 10^{-1} |
| 10^{-2} | 1 mm = 0.01 meters or 10^{-2} |
| 10^{-3} | 1 ml = 0.001 liters or 10^{-3} |

Seeing how negative exponents relate to real-world measurements can demystify their utility and application.
🌍 Note: Understanding the concept of scale through these examples can make negative exponents less abstract and more approachable.
4. Simplify Expressions with Negative Exponents

The manipulation of negative exponents becomes particularly useful when simplifying algebraic expressions. Here's how:
- Simplification: \frac{5^{-1}}{3^2} = \frac{\frac{1}{5}}{9} = \frac{1}{5 \times 9} = \frac{1}{45}.
- Combining like terms: 7^{-2} \times 7^{3} = 7^{-2 + 3} = 7^1 = 7.
- Using quotient rule: \frac{10^{-2}}{10^{4}} = 10^{-2-4} = 10^{-6} = \frac{1}{1,000,000}.
This ability to simplify expressions can be a game-changer in calculus and advanced algebra, where complex expressions often need to be broken down into manageable parts.
📝 Note: Simplification is not just about reducing an expression; it's about understanding its value and making mathematical operations smoother.
5. Regular Drills and Assessments

Learning mathematics is like training for a marathon; regular practice and self-assessment are key. Set aside time each day for:
- Quick Drills: Solve 10-15 negative exponent problems daily to build speed and accuracy.
- Self-Tests: Create or find practice tests online that focus on negative exponents. Review your mistakes and learn from them.
- Peer Learning: Find a study partner or join a study group to discuss and learn from each other's insights on negative exponents.
Regular practice not only helps in reinforcing concepts but also in identifying areas that need more attention.
🧐 Note: Don't shy away from making mistakes; they are an integral part of the learning process.
In the end, mastering negative exponents isn't just about memorizing rules; it's about understanding how these rules apply in a broader context. With these five tips—understanding the definition, practice through technology, real-life application, simplifying expressions, and regular practice—you'll find yourself navigating through the sea of negative exponents with ease and confidence.
The beauty of mathematics lies in its consistency and the seamless way it integrates with real-life applications. Negative exponents, though initially appearing challenging, reveal themselves as powerful tools for understanding fractions, measurements, and complex algebraic expressions. By practicing regularly, using visual aids, and connecting with real-life scenarios, you'll not only master negative exponents but also develop a deeper appreciation for the logic and beauty of mathematics.
What is a negative exponent?

+
A negative exponent represents a number being raised to a power and then inverted, turning it into a fraction where the exponent becomes positive.
Why are negative exponents useful?

+
They’re extremely helpful for simplifying complex mathematical operations, particularly when dealing with fractions and division in algebra and calculus.
Can negative exponents result in zero or negative numbers?

+
Negative exponents only apply to non-zero numbers. When a negative exponent is applied to a base number, it results in a fraction (where the numerator is one), never zero or negative numbers.
How do I simplify an expression with negative exponents?

+
To simplify, rewrite the term with the negative exponent as a fraction, then follow the rules of exponents to combine like terms or perform operations.