Name That Circle Part Worksheet Explained

Understanding the various parts of a circle can often seem daunting at first, but with a bit of explanation, it becomes much more manageable. Circles are essential shapes in geometry, found everywhere from art and architecture to the design of modern technology. Whether you're a student learning about circles for the first time or an enthusiast revisiting the basics, this guide aims to clarify each part of a circle through a detailed analysis of the "Name That Circle Part Worksheet."
Anatomy of a Circle

A circle is defined as a set of all points in a plane that are equidistant from a given point, known as the center. Here’s a breakdown of the key elements:
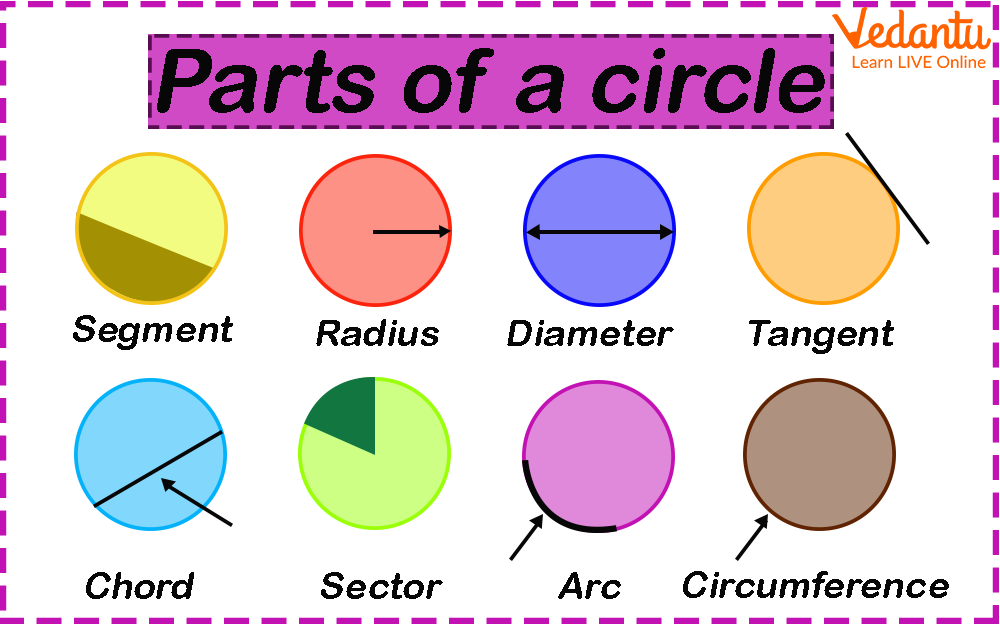
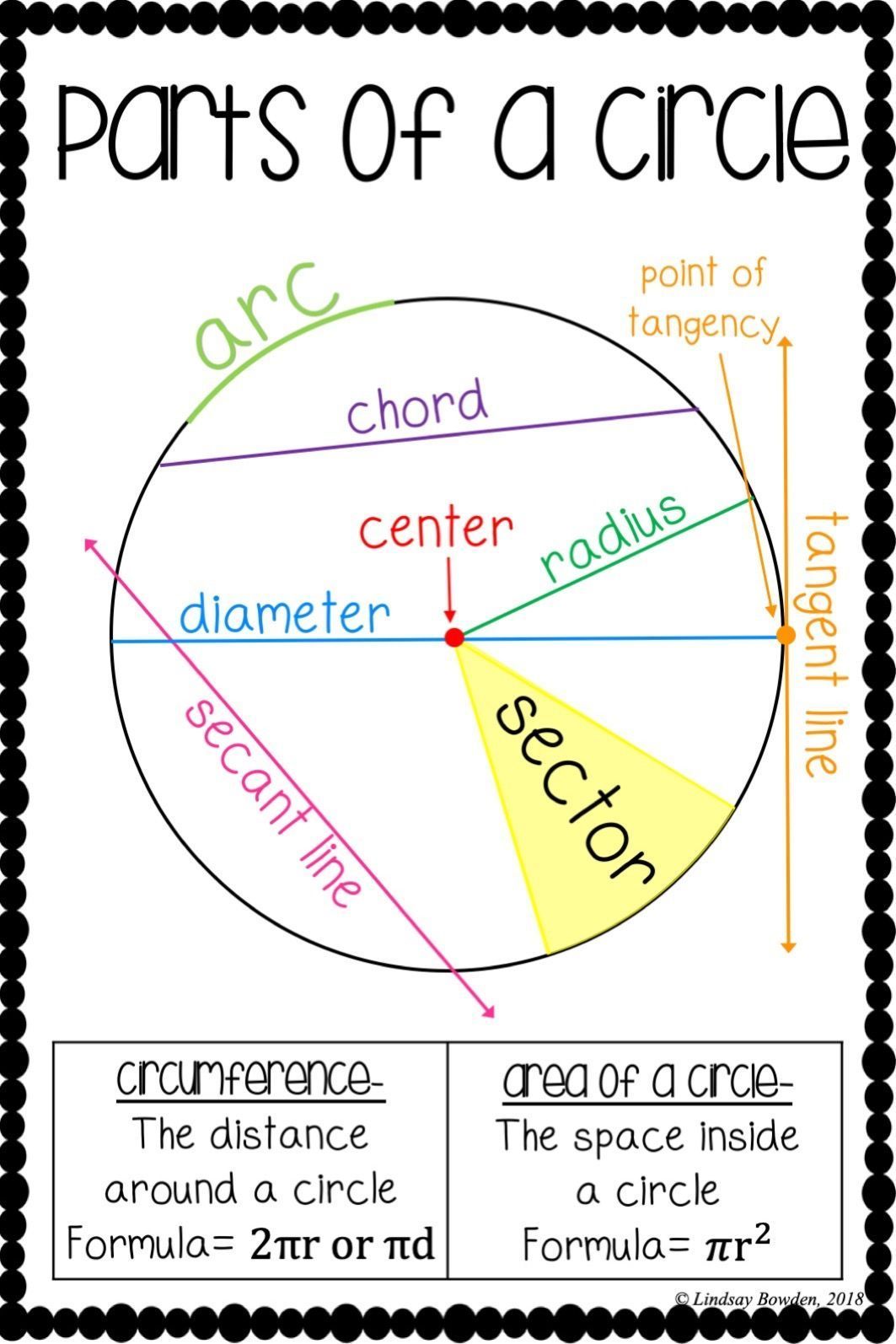
- Center: The central point that is equidistant from all points on the circle.
- Radius: The distance from the center to any point on the circle.
- Diameter: A line segment passing through the center, connecting two points on the circle's circumference; it's twice the length of the radius.
- Chord: A line segment whose endpoints lie on the circle, but unlike the diameter, does not necessarily pass through the center.
- Arc: A portion of the circumference of the circle.
- Sector: The area enclosed by two radii and the arc between them.
- Segment: The area enclosed by an arc and a chord.
- Tangent: A line that touches the circle at exactly one point.
- Secant: A line that intersects the circle at two points.
The Worksheet Approach

The “Name That Circle Part Worksheet” is designed to help learners identify and label these parts through visual aids and exercises. Here’s how a typical worksheet might look:
Circle Identification

Here, a simple circle will be presented. Students are tasked with:
- Marking the center.
- Measuring and labeling the radius.
- Finding and marking the diameter.
Labeling Chords, Arcs, Sectors, and Segments

After the basic parts:
- Students draw or identify multiple chords, labeling them.
- Arcs are identified, with distinctions between minor and major arcs explained.
- Sectors and segments are marked, helping to understand the different areas within a circle.
Working with Tangents and Secants

Advanced parts include:
- Drawing tangents to the circle and marking the point of tangency.
- Secants intersecting with the circle at two points, sometimes creating chords or dividing the circle into segments.
Understanding Formulas

While not always part of every worksheet, some include calculations such as:
- Area: A = \pi r^2
- Circumference: C = 2\pi r \text{ or } \pi d
🔍 Note: Pi (π) is approximately 3.14159 and is used in these formulas to calculate the circle's properties.
Strategies for Teaching and Learning
When using the "Name That Circle Part Worksheet":
- Visual Aids: Use diagrams to make abstract concepts more tangible.
- Hands-on Activities: Draw circles, measure with physical tools, or use manipulatives to understand spatial relationships.
- Real-life Examples: Point out circles in everyday objects (wheels, coins, pizza) to reinforce the concept's application.
- Group Work: Collaborative learning can enhance understanding through discussion and peer teaching.
🔍 Note: Engaging with circles in real life can make learning more relatable and less abstract.
Recap

Delving into the “Name That Circle Part Worksheet” offers a structured way to understand the circle’s anatomy, from the central point to the tangent and secant lines. By working through these exercises, students not only learn to label and calculate, but they also develop a deeper appreciation for the circular geometry that pervades our environment. This methodical approach promotes a clear understanding of each component’s role within the whole, ensuring a firm foundation for further exploration into the mathematical world or practical applications in design and engineering.
What is the difference between an arc and a chord in a circle?
+
An arc is a portion of the circumference of a circle, whereas a chord is a line segment whose endpoints are on the circle itself. While an arc is curved, a chord is straight.
Why is the diameter important?

+
The diameter is significant because it is the longest possible chord of a circle and also defines the circle’s width. It is twice the length of the radius and plays a key role in calculating the circle’s circumference and area.
Can a tangent be both a straight line and an arc?

+
No, a tangent to a circle is always a straight line that touches the circle at exactly one point, the point of tangency. An arc, on the other hand, is part of the circumference and not a line.