Answer Key: Colorful Angle Pair Names Worksheet Fun
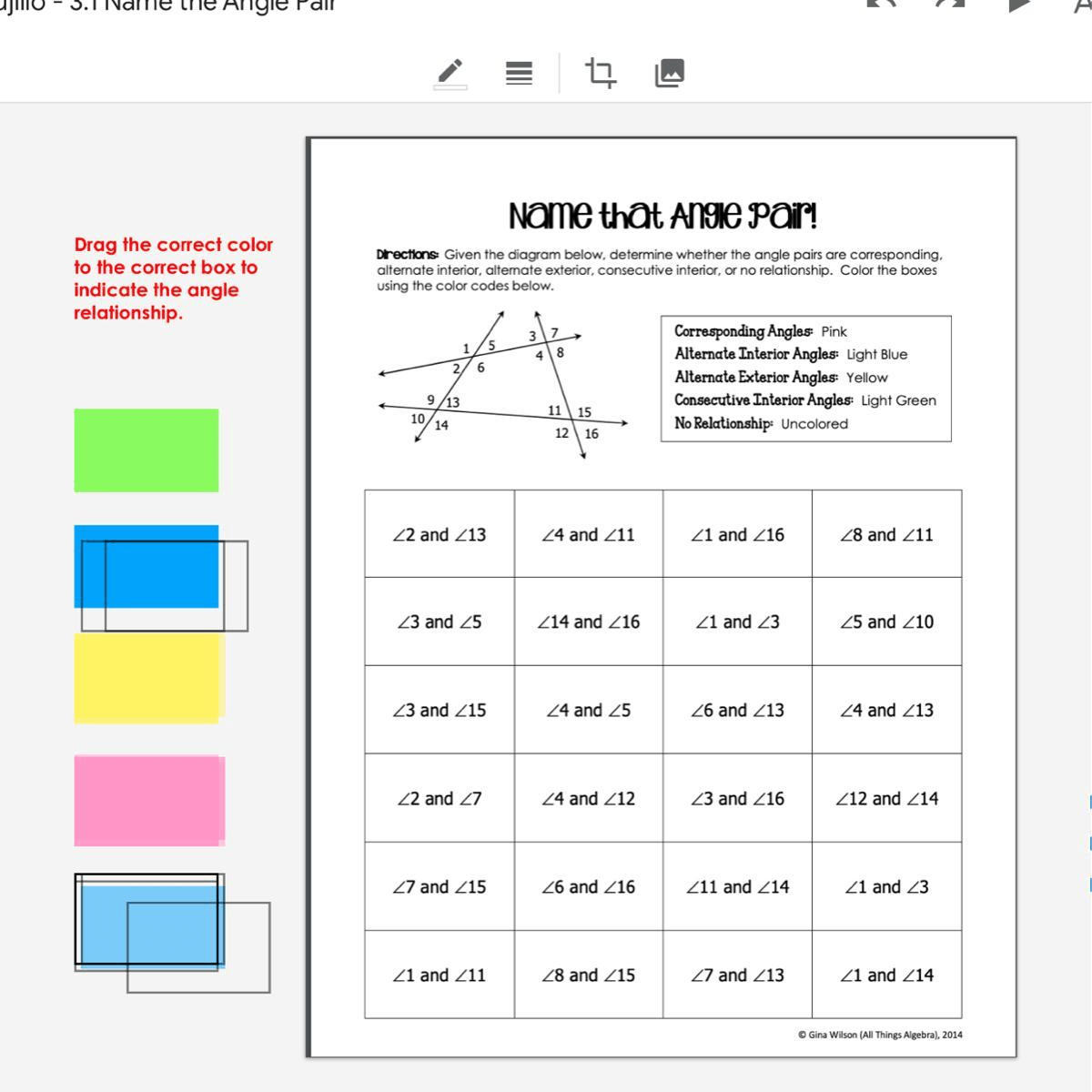
Understanding Complementary Angles

Complementary angles are a fundamental concept in geometry, especially when you’re starting to explore angle relationships. Here’s how you can think of them:
- Definition: Two angles are complementary if the sum of their measures equals 90 degrees.
- Visual Representation: Picture a right angle split into two parts, each angle being less than 90 degrees.
- Examples:
- Angles that are 30 degrees and 60 degrees.
- Angles that are 45 degrees and 45 degrees.
Remember, if you have an angle, you can find its complement by subtracting its measure from 90 degrees.

💡 Note: Complementary angles do not need to be adjacent. They can be anywhere, as long as their angles sum to 90 degrees.
Exploring Supplementary Angles

Next up, let’s talk about supplementary angles:
- Definition: Two angles are supplementary when their measures sum to 180 degrees.
- Visual Representation: Imagine a straight line, where one angle forms a part of this line, and the other completes it.
- Examples:
- An angle of 120 degrees with an angle of 60 degrees.
- Two right angles forming a straight line.
Keep in mind, like complements, supplementary angles don’t have to be adjacent. The key is the sum of their measures.

Linear Pairs and Vertical Angles

Now, let’s dive into some more complex angle pairs:
Linear Pairs

- Definition: A linear pair is a pair of adjacent angles on a straight line whose non-shared sides form a line.
- Characteristics: They always add up to 180 degrees, making them supplementary by definition.
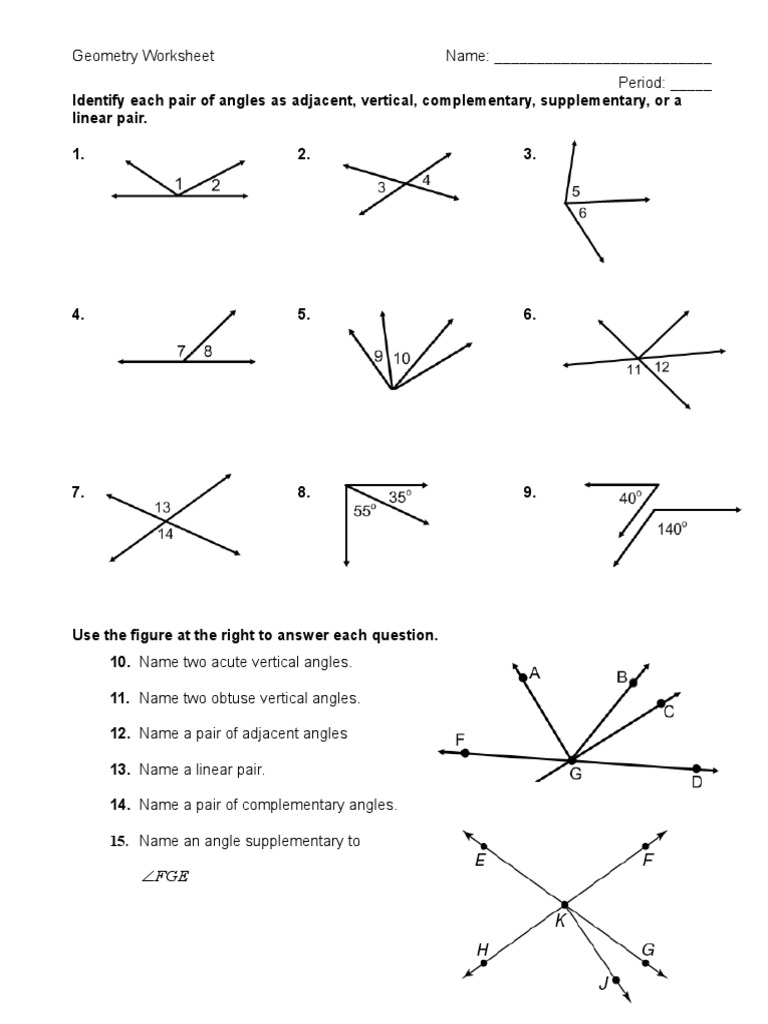
Vertical Angles

- Definition: Vertical angles are formed by two intersecting lines. They are the opposite angles created by these lines.
- Properties: Vertical angles are equal in measure because they are formed by the intersection.
Examples: - If you have two intersecting lines, the angles opposite each other will be equal. - This concept is often used to find missing angles in geometric figures.

🌟 Note: Vertical angles are an excellent way to find unknown angles, as they are always congruent.
Angle Chasers and Adjacent Angles
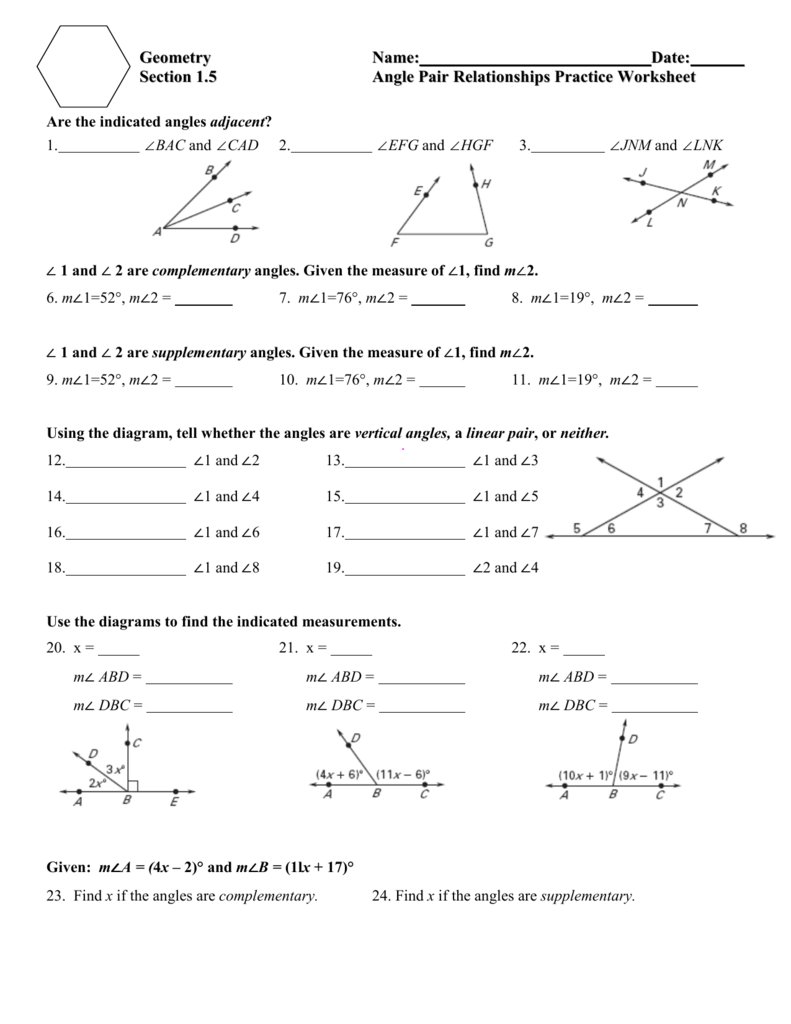
When dealing with angles, you’ll often come across these terms:
Angle Chasers

- Concept: Imagine you’re chasing the missing angles around geometric figures. This is where you apply all the rules about complementary, supplementary, linear, and vertical angles to solve problems.
Adjacent Angles

- Definition: Adjacent angles share a common vertex and a common side but do not overlap.
- Example: Think of two angles on a straight line where one angle forms the line, and the other completes it, but they share one side.
| Angle Type | Description |
|---|---|
| Complementary | Sum to 90 degrees |
| Supplementary | Sum to 180 degrees |
| Linear Pair | On a straight line, sum to 180 degrees |
| Vertical Angles | Opposite each other, equal in measure |
| Adjacent Angles | Share a common vertex and side, but not overlapping |

These relationships are not only foundational in understanding geometry but also help in problem-solving in various real-world applications.
In summary, the world of angle pairs is vibrant and full of interconnected rules and patterns. From complementary to supplementary, linear pairs to vertical angles, each type has its unique properties that can help you navigate through geometric problems. Remember:
- Complementary angles add up to 90 degrees.
- Supplementary angles sum to 180 degrees.
- Linear pairs are supplementary by their very nature.
- Vertical angles are congruent, providing a quick way to find unknown angles.
- Angle chasers use these relationships to solve for missing angles in complex figures.
How do you differentiate between complementary and supplementary angles?

+
Complementary angles sum to 90 degrees, while supplementary angles sum to 180 degrees.
Why are vertical angles always equal?
+
Vertical angles are formed by intersecting lines and are opposite each other, which inherently makes them equal in measure.
Can two adjacent angles be both complementary and supplementary?

+
No, two angles can be either complementary or supplementary, not both. They are different by definition.