5 Steps to Multiply Monomials Easily

Multiplying monomials might seem like a complex task at first, but with a structured approach, it becomes straightforward. Whether you're a student learning algebra or someone looking to refresh your math skills, understanding how to multiply monomials can simplify many mathematical operations. This guide will walk you through the 5 essential steps to master this operation with ease.
Understanding Monomials

Before diving into the multiplication process, it’s crucial to understand what monomials are:
- A monomial is an algebraic expression consisting of one term only, where the term can include coefficients, variables, and exponents.
- Examples: 5x, 3y², -2ab³, or 10 (where 10 is a constant considered as a monomial with a coefficient of 10 and no variables).
Step 1: Identify the Components

To multiply monomials, first:
- Identify the coefficients (the numerical parts).
- Identify the variables.
- Identify the exponents associated with each variable.
Step 2: Multiply the Coefficients

The multiplication begins with:
- Multiplying the numerical coefficients of the monomials directly. For example, if you have 4a and -2b, multiply 4 and -2 to get -8.
Step 3: Multiply the Variables
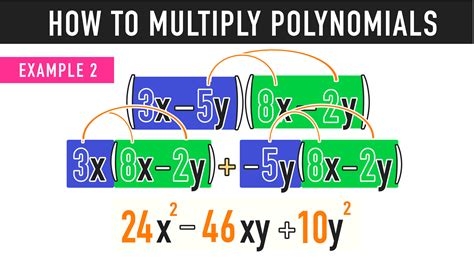
For the variable parts:
- Multiply the same variables together. For instance, if you’re multiplying x and y, you keep them as xy without changing their form.
- If there are multiple of the same variable, combine them by adding the exponents, as per the exponent rules.
Step 4: Apply Exponent Rules

When dealing with exponents:
- Add the exponents if the bases are the same. For example, x² * x³ = x^(2+3) = x⁵.
- Ensure that you only add exponents of variables with the same base. If variables are different, multiply them as they are.
Step 5: Combine and Simplify

After multiplying the components:
- Combine the results from Step 2, 3, and 4.
- Write down the product, ensuring all variables are in alphabetical order to keep it standardized.
✏️ Note: Always pay attention to the signs when multiplying coefficients, especially if they are negative.
Mastering the multiplication of monomials not only helps in solving algebraic equations but also sets the foundation for more complex polynomial operations. Remember that consistency in applying these steps will lead to accuracy and speed in your calculations. Whether for academic purposes or practical applications in fields like physics or engineering, these steps are indispensable for efficient problem-solving.
What is the difference between a monomial, binomial, and trinomial?

+
A monomial has one term, a binomial has two terms, and a trinomial has three terms. For example, 3x is a monomial, 2x + y is a binomial, and x² + 5x + 6 is a trinomial.
Can monomials have negative exponents?

+
Yes, monomials can have negative exponents. For instance, 3x⁻² is still considered a monomial. However, in standard form, negative exponents usually indicate division, so 3x⁻² would be equivalent to 3 / x².
How do you handle variables that appear in one monomial but not in the other?

+
If a variable appears in one monomial but not in the other, you simply include that variable with its exponent in the result of the multiplication. For example, if you multiply 2x by 5y, the result would be 10xy.