5 Ways to Simplify Multiplying Fractions Instantly

Multiplying fractions is one of the fundamental arithmetic operations, often encountered in school mathematics, daily life calculations, and advanced mathematical scenarios. Despite its apparent simplicity, many find themselves grappling with the basic steps involved. This blog post explores five effective methods to simplify multiplying fractions, ensuring the process is not only fast but also intuitive for readers of all skill levels.
Understanding Fraction Multiplication

Fraction multiplication involves multiplying the numerators together and the denominators together. The formula is straightforward:
(numerator of fraction 1) × (numerator of fraction 2) / (denominator of fraction 1) × (denominator of fraction 2)
However, before diving into the methods, let's ensure you understand the basic principles of fractions:
- Fractions represent parts of a whole, where the top number (numerator) indicates how many parts are taken and the bottom number (denominator) tells you how many equal parts the whole is divided into.
- The product of two fractions can often be simplified to a fraction in its lowest terms by dividing both the numerator and denominator by their greatest common divisor (GCD).
🤓 Note: Mastering the basics of fractions is crucial for efficiently understanding multiplication.
Method 1: Cross Multiplication

Cross multiplication simplifies the multiplication process by visually reorganizing the problem:
| Step | Action |
|---|---|
| 1 | Write the first fraction on the left and the second fraction on the right. |
| 2 | Multiply the numerator of the first fraction by the denominator of the second (this will be the new numerator). |
| 3 | Multiply the numerator of the second fraction by the denominator of the first (this will be the new denominator). |
This method reduces the number of steps and visualizes the multiplication better:
💡 Note: Cross multiplication is particularly helpful for visual learners who prefer a graphical approach.
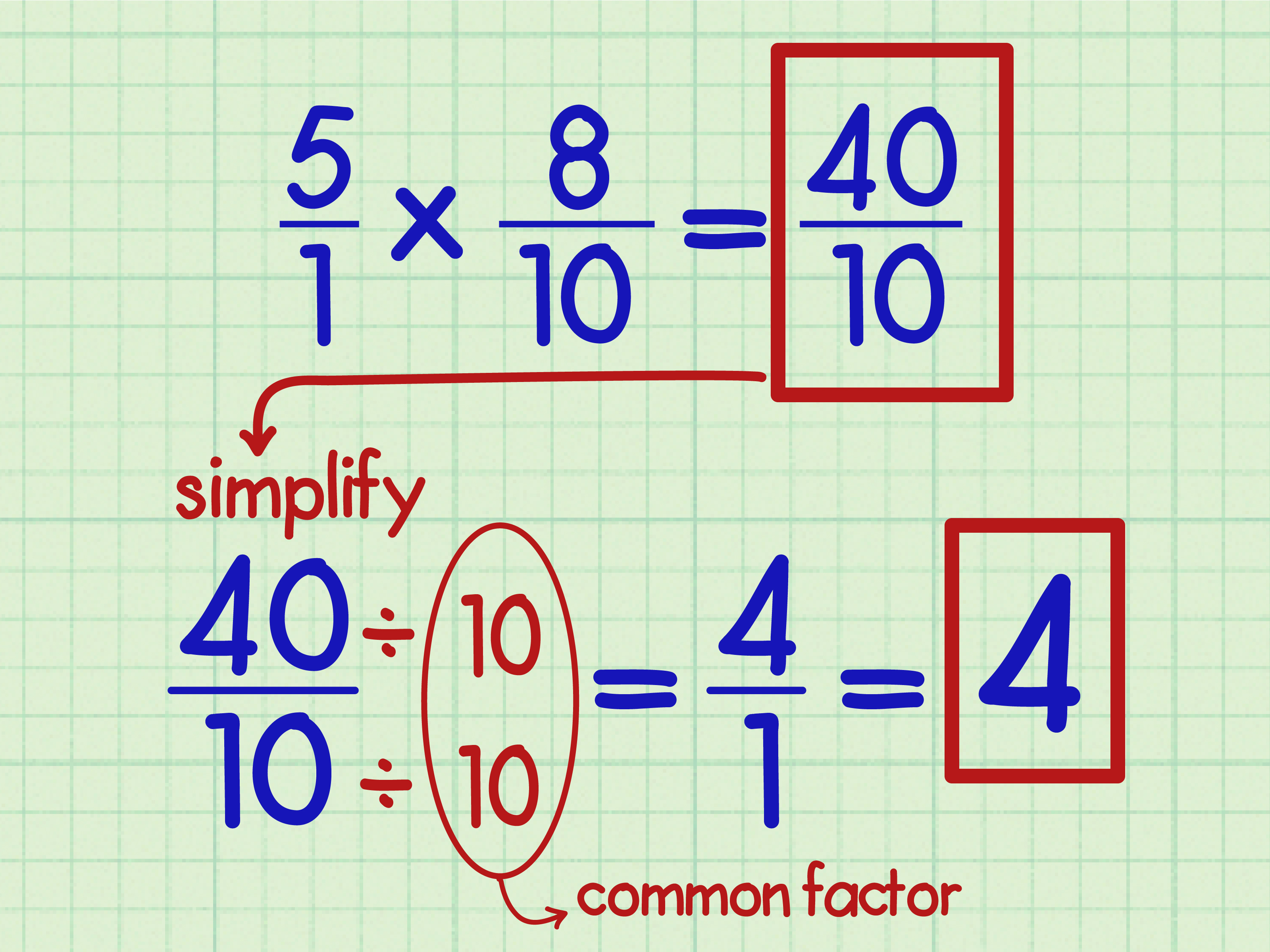
Method 2: Simplifying Before Multiplication

Before multiplying fractions, it's beneficial to simplify:
- Find the greatest common divisor (GCD) between the numerator and the denominator of one or both fractions.
- Divide both the numerator and the denominator of each fraction by their GCD before multiplying.
Simplification reduces the magnitude of the numbers being multiplied, making the subsequent calculation easier.
Method 3: Using the Fraction Diamond

The fraction diamond is a diagrammatic representation that:
- Positions the numerator of one fraction at the top left and the denominator at the bottom left.
- Places the second fraction similarly on the right.
- The product is found where the two diagonals intersect.
This method aids in visualizing the multiplication process:

🌟 Note: The Fraction Diamond method works particularly well for those who understand visual cues.
Method 4: Applying Greatest Common Factors

When multiplying more than two fractions:
- Identify the common factors among all numerators and denominators.
- Use these to simplify all the fractions before multiplying.
This technique not only reduces the numbers involved but also ensures the product is in its simplest form.
Method 5: The LCM and GCD Method

Here, you:
- Find the least common multiple (LCM) of the denominators to simplify the process.
- Identify the greatest common divisor (GCD) between the numerators and denominators for simplification.
- Multiply the simplified fractions together.
This method minimizes the numbers you work with:
🔍 Note: Using LCM and GCD ensures the product is as simple as possible, reducing potential errors in subsequent steps.
These five methods not only simplify the process of multiplying fractions but also enhance understanding by offering visual and numerical shortcuts. Each method has its advantages, depending on the fractions involved and the individual's learning style.
By practicing these methods, one can become adept at fraction multiplication, turning what many see as a chore into an engaging mental exercise. The key is to practice regularly, understand the underlying principles of fractions, and find which method resonates with your way of learning and thinking. Whether you're a student revisiting basic math or an adult looking to refresh your arithmetic skills, these techniques can make multiplying fractions not only more intuitive but also, dare we say, fun.
Why is it important to simplify fractions?

+
Simplifying fractions reduces the complexity of calculations, making it easier to work with smaller numbers, and ensures the fraction is in its lowest terms, which is critical in many mathematical operations and real-world applications.
Can I use a calculator to multiply fractions?

+
Yes, you can use a calculator that has fraction capabilities. However, understanding the manual methods is beneficial for problem-solving and mental agility.
What if I encounter improper fractions?

+
Improper fractions (where the numerator is greater than the denominator) can be multiplied just like proper fractions. However, after multiplication, you might want to convert the product back to a mixed number for clarity.