5 Steps to Master Multiplying Fractions and Mixed Numbers

Multiplying fractions and mixed numbers can often seem like a daunting task for many students, yet with the right techniques and understanding, it can become a straightforward process. In this detailed guide, we will explore the essential steps to master multiplying fractions and mixed numbers, ensuring you can tackle any problem with confidence. From simplifying to avoiding common mistakes, we've got you covered.
Step 1: Understanding Fractions and Mixed Numbers

Before we delve into multiplication, let’s review what we mean by fractions and mixed numbers:
- Fractions are numbers that represent part of a whole. They consist of a numerator (the top number) and a denominator (the bottom number), e.g., 3⁄4.
- Mixed Numbers combine whole numbers and fractions. For instance, 1 3⁄4 is a mixed number because it comprises the whole number “1” and the fraction “3⁄4”.

Step 2: Converting Mixed Numbers to Improper Fractions
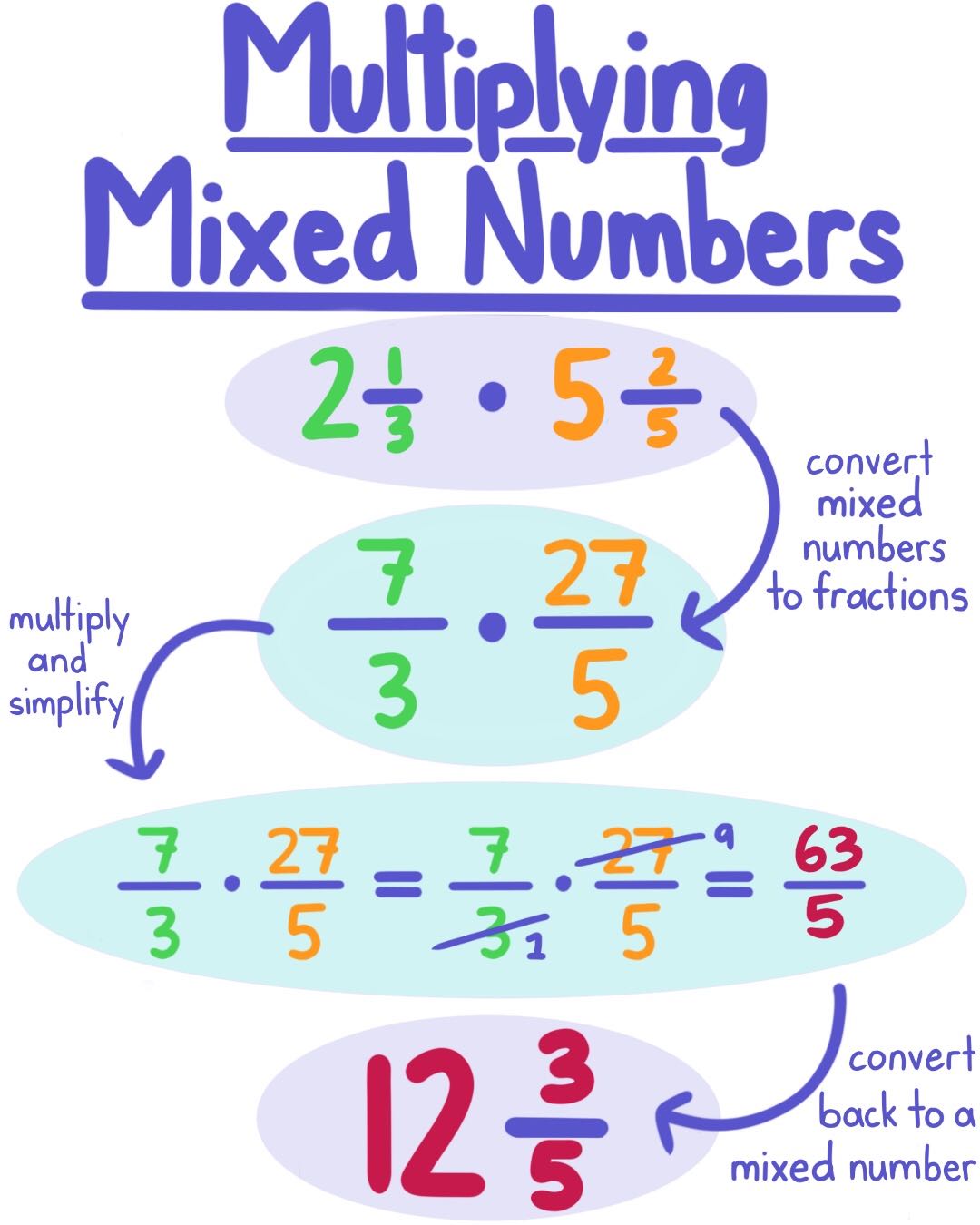
To multiply mixed numbers with fractions, we need to convert them to improper fractions:
- Take the whole number and multiply it by the denominator of the fraction.
- Add this product to the numerator to get the new numerator.
- Keep the original denominator.
Here’s how to convert 1 3⁄4 to an improper fraction:
- 1 * 4 = 4 (denominator * whole number)
- 4 + 3 = 7 (new numerator)
- 7⁄4 (our improper fraction)

📝 Note: When converting mixed numbers to improper fractions, ensure the fractions are reduced to their simplest form if possible before multiplication.
Step 3: Multiplying Fractions

After converting, multiply the fractions:
- Multiply the numerators together.
- Multiply the denominators together.
- The product of these two steps gives you the result in fraction form.
For example, multiplying 3⁄4 by 7⁄4:
- Numerators: 3 * 7 = 21
- Denominators: 4 * 4 = 16
- Result: 21⁄16

📝 Note: Remember to simplify the result if possible. Here, 21⁄16 is already in its simplest form.
Step 4: Converting Back to Mixed Numbers (If Necessary)

After multiplication, you might want to convert the improper fraction back to a mixed number:
- Divide the numerator by the denominator.
- Write the quotient as the whole number, the remainder as the new numerator, and keep the original denominator.
Let’s take 21⁄16 from the previous step:
- 21 ÷ 16 = 1 (quotient) with a remainder of 5
- The mixed number is 1 5⁄16

Step 5: Review and Practice

Practicing these steps ensures you master multiplying fractions and mixed numbers:
- Understand the concept of fractions and mixed numbers thoroughly.
- Convert mixed numbers to improper fractions before multiplying.
- Multiply the numerators and denominators separately.
- Convert back to mixed numbers if necessary.
Regular practice and understanding these key points will help you master this mathematical operation:
| Step | Description |
|---|---|
| 1 | Understand fractions and mixed numbers |
| 2 | Convert mixed numbers to improper fractions |
| 3 | Multiply fractions |
| 4 | Convert back to mixed numbers if necessary |
| 5 | Regular practice |

📝 Note: Multiplying fractions and mixed numbers can seem intimidating, but with consistent practice, you’ll see how intuitive it can be.
To summarize, mastering the multiplication of fractions and mixed numbers involves understanding basic concepts, converting between forms, performing straightforward multiplication, and converting back when needed. By following these steps, not only will you excel in this area of mathematics, but you'll also build confidence in your problem-solving abilities, enhancing your overall mathematical competence.
Why do we convert mixed numbers to improper fractions before multiplying?

+
Mixed numbers are not directly multiplicable with standard fractions. Converting them to improper fractions allows for a uniform approach to multiplication, making the process simpler and more consistent.
Can I multiply fractions with whole numbers directly?

+
Yes, you can. Whole numbers can be thought of as fractions with a denominator of 1, so you can multiply them directly with fractions by treating the whole number as a fraction. For example, 3 * 1⁄2 = 3⁄1 * 1⁄2 = 3⁄2 or 1 1⁄2.
What’s the importance of simplifying the result?

+
Simplifying ensures the fraction is in its most reduced form, making it easier to understand and work with. This step avoids dealing with unnecessarily large numbers, simplifying calculations, and enhancing clarity.