Master Scientific Notation: Multiply and Divide Practice

Understanding scientific notation is not just about grasping a mathematical concept; it's about comprehending a tool used across various scientific disciplines. Scientific notation offers a way to handle very large or very small numbers with ease, making calculations in chemistry, physics, astronomy, and many other fields straightforward and manageable. This guide aims to demystify how to multiply and divide numbers expressed in scientific notation, ensuring you not only understand the principles but can apply them effectively.
The Basics of Scientific Notation

Before we dive into operations, let’s refresh the essentials of scientific notation:
- Form: A number is written as a x 10b, where 1 ≤ a < 10, and b is an integer.
- Why Use It: It simplifies numbers like 0.000045 or 45,000,000 to 4.5 x 10-5 or 4.5 x 107 respectively, making them easier to compare, read, and calculate with.
Multiplying Numbers in Scientific Notation
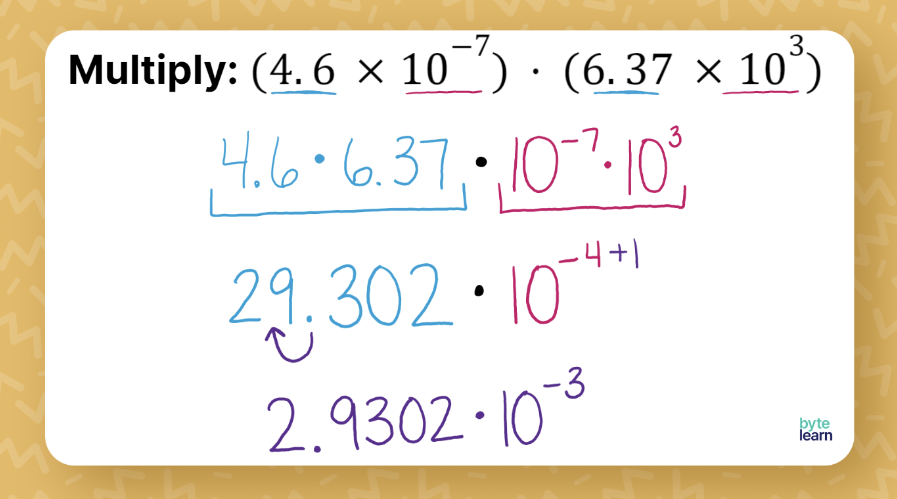
Multiplying in scientific notation involves:
- Step 1: Multiply the mantissas (the numbers).
- Step 2: Add the exponents of the base (10).
- Step 3: Convert the result back to standard scientific notation if necessary.
Let's consider an example:
- Example: Multiply 3.2 x 104 by 5.6 x 106
- 3.2 * 5.6 = 17.92
- 4 + 6 = 10
- 17.92 x 1010 = 1.792 x 1011
🔎 Note: Ensure your result is in proper scientific notation, adjusting the decimal point and exponent as needed.
Dividing Numbers in Scientific Notation

Dividing in scientific notation involves:
- Step 1: Divide the mantissas.
- Step 2: Subtract the exponent of the denominator from the exponent of the numerator.
- Step 3: Again, convert back to standard scientific notation if necessary.
Here's an example:
- Example: Divide 8.4 x 108 by 2.1 x 103
- 8.4 ÷ 2.1 = 4
- 8 - 3 = 5
- The result is 4 x 105
📌 Note: Always keep track of the base 10 when handling exponents in division.
Tips for Mastering Scientific Notation

- Practice: Regularly work through exercises to solidify your understanding.
- Use Tools: Calculators with scientific notation functions can be useful for verification.
- Conversion Skill: Develop quick mental conversion from regular numbers to scientific notation and vice versa.
- Understand Significance: Know how many significant figures your answers should retain.
🎓 Note: Learning to convert between scientific notation and regular numbers quickly is vital for exams and practical applications.
Understanding the mechanics of multiplying and dividing in scientific notation can significantly enhance your proficiency in scientific calculations. Here are some key points to remember:
- Multiplying involves multiplying the mantissas and adding the exponents.
- Dividing involves dividing the mantissas and subtracting the exponent of the denominator from that of the numerator.
- Conversion to standard scientific notation is crucial after performing these operations.
Having a clear grasp of these concepts allows you to tackle complex scientific problems with confidence. From measuring microscopic phenomena in physics to calculating astronomical distances, scientific notation remains an indispensable tool for scientists and students alike.
Why do we use scientific notation?

+
Scientific notation is used to express very large or very small numbers in a way that’s easier to handle and understand, making mathematical operations simpler and reducing the likelihood of errors.
How do you convert from standard notation to scientific notation?

+
To convert from standard notation to scientific notation, move the decimal point until the number is between 1 and 10. Count how many places you moved the decimal point, and this will be the exponent of 10. If the decimal is moved to the left, the exponent is positive; if to the right, it’s negative.
What are significant figures and why are they important in scientific notation?

+
Significant figures indicate the precision of a number. When multiplying or dividing numbers in scientific notation, the result should have no more significant figures than the number with the least significant figures involved in the calculation.