Mastering Multiplication: Scientific Notation Worksheet

Scientific notation is a powerful tool used to represent very large or very small numbers in a more manageable way. Whether you're a student grappling with math homework or a scientist dealing with complex calculations, understanding how to use and manipulate numbers in scientific notation is crucial. Today, we delve into the specifics of creating and using scientific notation worksheets for multiplication, offering you a step-by-step guide to mastering this essential skill.
Why Scientific Notation?

Scientific notation simplifies the task of dealing with numbers of vastly different scales. Here’s why it’s invaluable:
- Efficiency: It’s quicker and less error-prone to write 3.5 × 108 than 350000000.
- Comparability: Numbers in scientific notation can be easily compared, as they all have a similar form.
- Accuracy: Calculations with numbers that differ by orders of magnitude become more precise.
- Universal Language: Scientists worldwide use it for consistency and clarity in communication.
Understanding Multiplication in Scientific Notation

Multiplying numbers in scientific notation involves three main steps:
- Multiply the Coefficients: Treat the numbers as regular decimals or integers.
- Add the Exponents: Since you’re dealing with powers of 10, you add the exponents directly.
- Normalize the Result: Ensure your result is in scientific notation by adjusting the decimal point and exponent if necessary.
Creating Your Scientific Notation Worksheet

Let’s walk through the process of creating a worksheet that not only teaches but also reinforces the concept of multiplication using scientific notation:
Step 1: Setting the Foundation

Begin with basic multiplication examples:
- (3.0 × 103) × (2.0 × 102)
- (4.5 × 10-6) × (7.0 × 10-5)
💡 Note: Start with positive integers for coefficients to ease into the concept.
Step 2: Progressing to Mixed Numbers

Introduce examples with negative exponents or fractional coefficients:
- (3.0 × 103) × (4.0 × 10-1)
- (2.45 × 102) × (3.0 × 10-1)
Step 3: Challenging with Real-World Applications

Use numbers from actual scientific or engineering applications:
- The speed of light (approximately 3 × 108 meters per second) × The distance from Earth to Sun (1.5 × 1011 meters).
- Planck’s constant (6.626 × 10-34 J·s) × 2.45 × 103 (frequency in Hz).
Step 4: Interactive Elements

Incorporate interactive tasks where students:
- Match answers with scientific notation problems.
- Convert from standard form to scientific notation before multiplying.
- Estimate the product before calculating precisely.
Advanced Topics

Once your students are comfortable with basic multiplication, introduce more complex scenarios:
Negative and Fractional Exponents

Introduce problems like:
- (4.0 × 10-2) × (3.0 × 10-3)
- (1.2 × 10-4) × (3.5 × 101)
🧮 Note: Emphasize how adding negative exponents results in a smaller number, but still in scientific notation form.
Working with Units

Incorporate units to make problems more realistic:
- (2.0 × 104 meters) × (3.5 × 102 meters/second) = ? Joules
Worksheet Examples
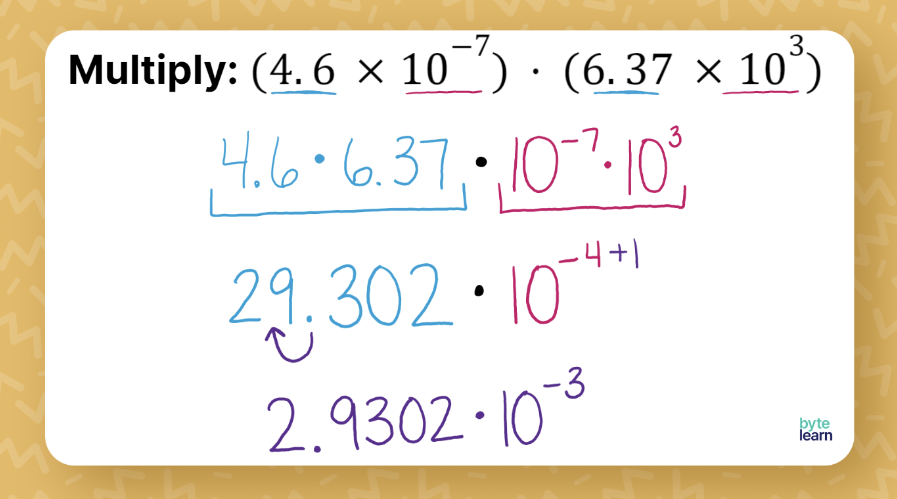
Here’s a table to help you create or visualize your own worksheet:
| Problem | Solution |
|---|---|
| (5.0 × 105) × (3.0 × 104) | 1.5 × 1010 |
| (1.5 × 103) × (2.0 × 10-2) | 3.0 × 101 |
| (4.5 × 10-6) × (7.0 × 10-5) | 3.15 × 10-10 |
| The mass of the Sun (1.989 × 1030 kg) × The gravitational constant (6.674 × 10-11 m³·kg-1·s-2) = ? | 1.327 × 1020 N |

Conclusion

By following this structured approach to creating and using scientific notation multiplication worksheets, you set up an engaging learning environment for students to understand and appreciate the utility of scientific notation. Through practical examples, real-world applications, and interactive tasks, learners can internalize these concepts. The journey from basic multiplication to handling complex scenarios with ease not only boosts confidence but also lays a solid foundation for further mathematical and scientific exploration.
Why do we use scientific notation?

+
Scientific notation helps in dealing with extremely large or small numbers efficiently, making them easier to compare, calculate, and communicate.
How do you add exponents in scientific notation multiplication?

+
In scientific notation multiplication, you add the exponents of the numbers’ powers of 10. For example, (3.0 × 104) × (2.0 × 103) results in an exponent of 4 + 3 = 7, giving you (6.0 × 107).
Can you multiply negative exponents in scientific notation?

+
Yes, you can multiply negative exponents in scientific notation just like you would with positive ones. Add the exponents, keeping track of the signs. If both exponents are negative, their sum will be negative, resulting in a smaller number.