5 Tricks to Master 2-Digit by 1-Digit Multiplication Fast

Have you ever been in a situation where you're trying to crunch numbers quickly but find yourself stuck? Maybe it's calculating change at a store, estimating project costs, or simply doing mental arithmetic faster than your calculator-loving friends. If the answer is yes, then learning to master 2-digit by 1-digit multiplication can be your secret weapon. Here, we'll explore five clever tricks to help you multiply numbers like a pro, enhancing your mental math skills significantly.
1. The Break-and-Multiply Technique

This method breaks the larger number into tens and units, making multiplication much simpler. Here’s how you do it:
- Break the 2-digit number into its tens and units.
- Multiply each part by the 1-digit number.
- Add the results together.
Let’s take an example: Multiplying 34 by 5
- Break: 34 becomes 30 and 4
- Multiply: 30 x 5 = 150, 4 x 5 = 20
- Add: 150 + 20 = 170
💡 Note: This trick works great when you want to multiply larger numbers by a small 1-digit number quickly.
2. The Finger Multiplication Method

If you’re more of a visual learner, the Finger Multiplication Method might be perfect for you. This is especially useful for people who like to have a tangible way to visualize multiplication:
- Hold up your hands with fingers spread.
- Assign numbers to each finger, starting with 6 on your left thumb up to 10 on your right little finger.
- To multiply a 1-digit number with a 2-digit number that’s greater than 10, use the fingers to represent the units place of the number:
- For the 1-digit number, let’s say 8, raise the left thumb (since it represents 6, add 2 to get 8) and the left index finger (since it represents 8, so we know it corresponds to 8).
- For the 2-digit number, like 13, where the units place is 3, raise the right ring finger (3rd finger) to represent 9.
- Multiply the number represented by the raised fingers, which are 8 (from left thumb and index) and 9 (from right ring). That’s 72.
- Count how many fingers are raised before the right ring finger. In this case, there are 3 fingers (since we’ve raised 6 and 8 from the left hand and 9 from the right hand).
- Add these two numbers: 72 + 30 = 102
3. The Compensation Method

When one of the numbers ends in a 9 or an 8, you can use this trick to simplify:
- If the 1-digit number is 9, add 1 to the other number and then subtract the 1-digit number from the result.
- If the 2-digit number ends in 9, round it to the next multiple of 10, multiply, and then subtract the 1-digit number times the ones place.
Let’s take an example: Multiplying 48 by 9
- Round: 48 rounded up to 50
- Multiply: 50 x 9 = 450
- Compensate: Subtract 450 - (9 x 2) = 450 - 18 = 432
4. Using Algebraic Magic

Algebra can be a handy tool even in mental math. Here’s how:
- Let x be the 2-digit number and y be the 1-digit number.
- The product is xy = (10a + b) * y, where a and b are the tens and units digits of x.
- Simplify: (10a + b) * y = 10ay + by.
- Example: Multiplying 23 by 7
- Here, x = 23 and y = 7.
- So, (10 * 2 + 3) * 7 = (20 + 3) * 7 = 23 * 7
- The product is 20*7 + 3*7 = 140 + 21 = 161
5. The Double-Digit Shortcut

Sometimes, using known facts can speed up the process:
- If the 2-digit number ends in 5, multiply the tens place by one more than the 1-digit number and then add half of the 1-digit number.
Let’s take an example: Multiplying 45 by 6
- Multiply: 4 (tens place) by (6 + 1) = 4 * 7 = 28.
- Add: Add 280 + 30 = 310. (28 * 10 since we're dealing with tens place, plus half of 6, which is 3, times 10).
💡 Note: This trick leverages the rule of 5 multiplication, making complex multiplication simpler.
These tricks and methods aren’t just about making multiplication faster; they're also about understanding the underlying mathematics, which can boost your confidence in handling numbers in everyday scenarios or in more complex calculations. By practicing these techniques, you'll find that your ability to perform 2-digit by 1-digit multiplication mentally will improve significantly, and you might even surprise yourself with your newfound math prowess.
Can these multiplication tricks be applied to larger numbers?

+
Yes, while these tricks are primarily designed for 2-digit by 1-digit multiplication, the underlying principles can be adapted for larger numbers with some practice.
What if the 1-digit number is larger than 9?
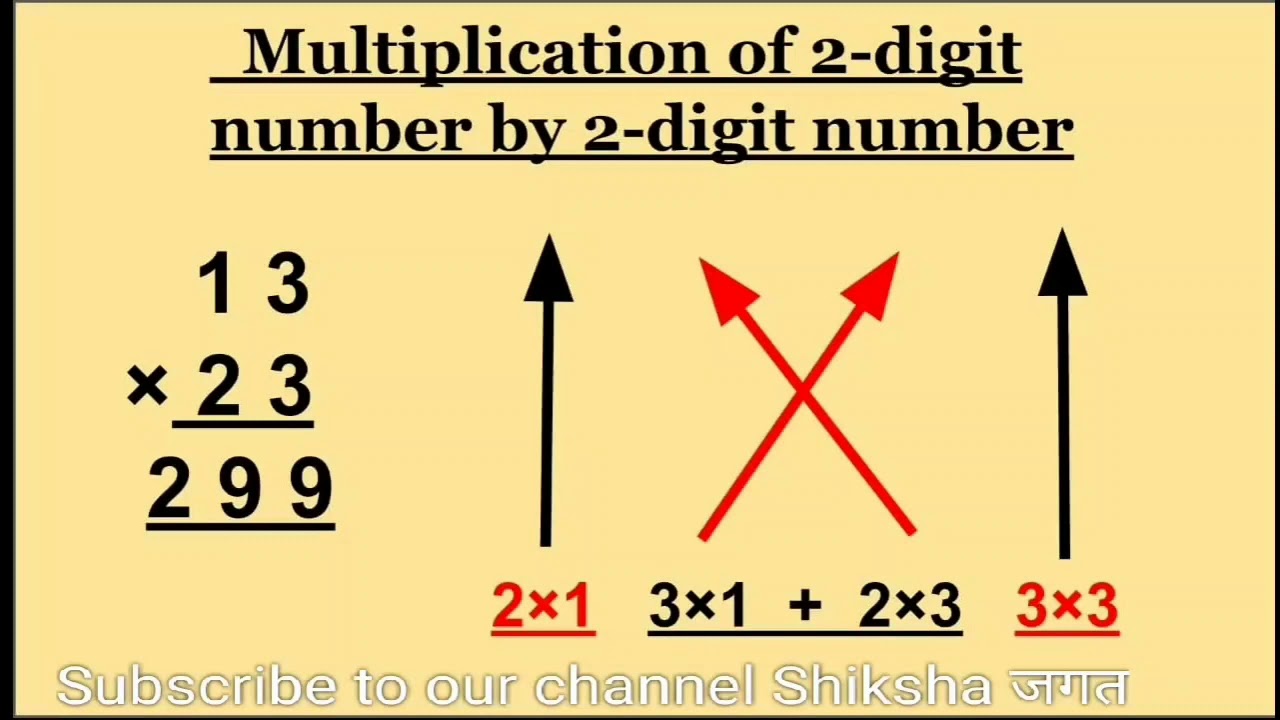
+
These tricks are less efficient when the 1-digit number is greater than 9. However, you can decompose the number into two digits and apply these methods separately.
How long does it take to master these techniques?
+
It varies from person to person, but with consistent practice, most people can start seeing improvements within a week.
Are there any digital tools to help practice these methods?
+
Yes, there are various mental math apps and websites that offer interactive exercises specifically for these types of multiplication techniques.