5 Tips for Solving Multi-Step Equations Easily

Mastering multi-step equations is crucial for students at the middle and high school levels. Understanding these equations can simplify more advanced mathematical concepts and improve problem-solving skills. Here, we'll delve into five effective tips that will not only make solving multi-step equations easier but also boost your confidence in tackling algebra.
Tip 1: Start with the Simplest Steps
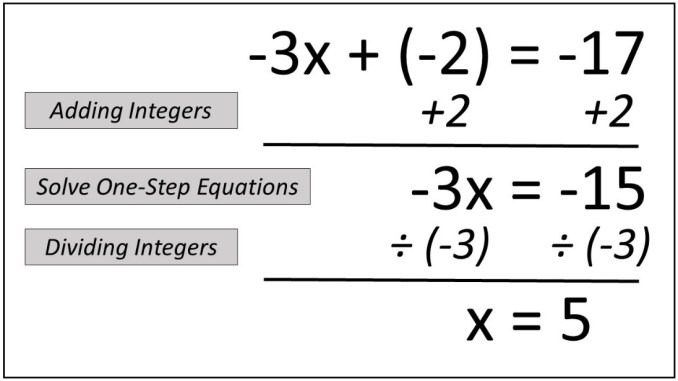
When faced with a multi-step equation, begin by focusing on the simplest operations you can perform:
- Combine like terms on both sides of the equation to reduce complexity.
- Isolate variables by removing constants or like terms using addition or subtraction.
- Eliminate coefficients by dividing or multiplying both sides by the same number.

💡 Note: This approach reduces the cognitive load by breaking down the equation into more manageable parts.
Tip 2: Keep Both Sides Balanced

A fundamental rule of algebra is to maintain the equation’s balance:
- If you add or subtract something from one side, do the same on the other side.
- Multiplication or division also needs to be consistent across both sides of the equation.
- Double-check your work to ensure both sides remain equal after each step.
Tip 3: Use the Distributive Property Wisely

The distributive property can be a powerful tool:
- Distribute the multiplication or division to every term inside parentheses.
- Identify when to use the property to simplify complex terms.
- After distribution, combine like terms to further simplify the equation.

Tip 4: Check Your Work

Accuracy in algebra is paramount:
- Plug your solution back into the original equation to verify its correctness.
- Review each step to ensure no mistakes were made in simplifying or solving.
- Look out for common errors like sign mistakes or overlooking like terms.
Tip 5: Practice with Real-World Problems

Applying equations to real-world scenarios can:
- Enhance understanding of how equations model real situations.
- Improve your ability to set up and solve practical problems.
- Make abstract algebra concepts more tangible and relatable.

🔍 Note: Real-world applications help bridge the gap between theory and practice, making algebra more engaging.
In summary, mastering multi-step equations involves starting with the simplest steps, maintaining balance, using the distributive property efficiently, double-checking your work, and applying these skills to real-world problems. By implementing these tips, you'll not only solve equations with ease but also develop a deeper understanding of algebra, which can be incredibly useful in various academic and professional fields.
What are common mistakes in solving multi-step equations?

+
Frequent errors include forgetting to perform the same operation on both sides, misapplying the distributive property, or making sign mistakes during simplification.
How can I become better at solving these equations quickly?

+
Regular practice, understanding the underlying principles, and applying shortcuts like recognizing patterns in equations will help increase your speed.
Is it necessary to check my work after solving an equation?

+
Yes, checking your solution back in the original equation ensures accuracy and helps catch any algebraic errors or oversights.