5 Steps to Solve Multi-Step Equations Easily

Introduction to Multi-Step Equations

Have you ever struggled to solve equations with multiple steps? Fear not! Solving multi-step equations can be as straightforward as piecing together a puzzle. Understanding how to approach these problems not only simplifies them but also enhances your problem-solving skills. Let’s delve into the five key steps you can use to tackle these equations with ease.
Step 1: Clear Fractions or Decimals

The first step in solving multi-step equations is to clear any fractions or decimals, which can complicate your calculations. Here’s how you do it:
- Identify all fractions or decimals in the equation.
- To clear fractions, multiply both sides of the equation by the least common denominator (LCD). This makes the fractions disappear, allowing you to work with whole numbers.
- If decimals are present, multiply by a power of 10 to convert them into whole numbers. For example, to remove two decimal places, multiply by 100.
⚠️ Note: Remember, what you do to one side of the equation, you must do to the other to maintain equality.
Step 2: Use the Distributive Property

If your equation includes parentheses, use the distributive property to simplify:
- Distribute any numbers outside the parentheses to each term inside.
- This step helps in combining like terms and reducing the complexity of your equation.
| Expression | Action | Result |
|---|---|---|
| 3(x + 2) | Distribute 3 | 3x + 6 |
| -2(3y - 7) | Distribute -2 | -6y + 14 |

Step 3: Combine Like Terms

After distributing, you’ll often find multiple terms that can be combined:
- Add or subtract the like terms on each side of the equation.
- Look for variables with the same exponent or constants that can be merged together.
✨ Note: If you have terms like x, 2x, and 3x on the same side, these can be combined to make 6x.
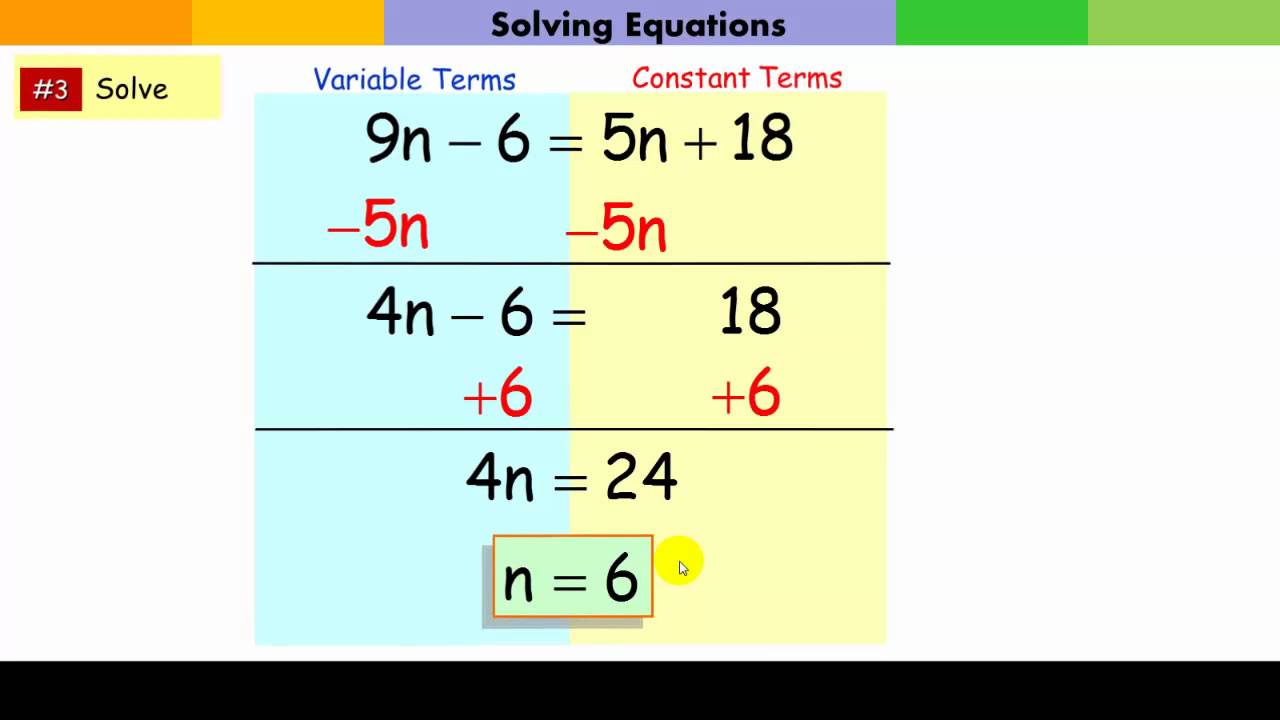
Step 4: Isolate the Variable

The next step involves isolating the variable on one side of the equation:
- If you have a variable on both sides, add or subtract the variable to eliminate it from one side.
- Once you have the variable isolated, perform inverse operations to solve for it. For instance, if x is multiplied by 5, divide by 5 to find x.
Step 5: Check Your Solution

Verification is crucial in mathematical problem-solving:
- Substitute the value you found for x back into the original equation.
- If both sides of the equation balance out, your solution is correct. If not, you might need to recheck your steps or review the problem for possible errors.
The process of solving multi-step equations might seem daunting at first, but breaking it down into these five steps makes it manageable. Each step builds on the previous, leading you through a logical path to the solution. Whether you're dealing with basic algebra or more complex problems, this approach ensures you cover all the necessary bases.
In wrapping up, remember that practice is the key to proficiency in mathematics. The more you practice solving multi-step equations, the more intuitive the process will become. Keep these steps in mind, and you’ll not only solve equations faster but also with greater accuracy. Happy problem-solving!
Why is it important to clear fractions or decimals first?

+
Clearing fractions or decimals simplifies the equation, making it easier to perform operations like addition or subtraction, which are critical in later steps.
What is the distributive property and why is it useful?

+
The distributive property allows you to distribute a number or variable across terms inside parentheses, simplifying complex expressions and aiding in the combination of like terms.
Can I skip any of these steps if my equation is simpler?

+
Yes, if your equation does not require clearing fractions or decimals, or if it already has no parentheses, you might skip these steps, but always ensure you follow the logic of the equation to avoid errors.
Why do I need to check the solution?
+
Checking the solution confirms that the value you found for the variable makes the original equation true, ensuring your math is accurate and your problem-solving approach was correct.



