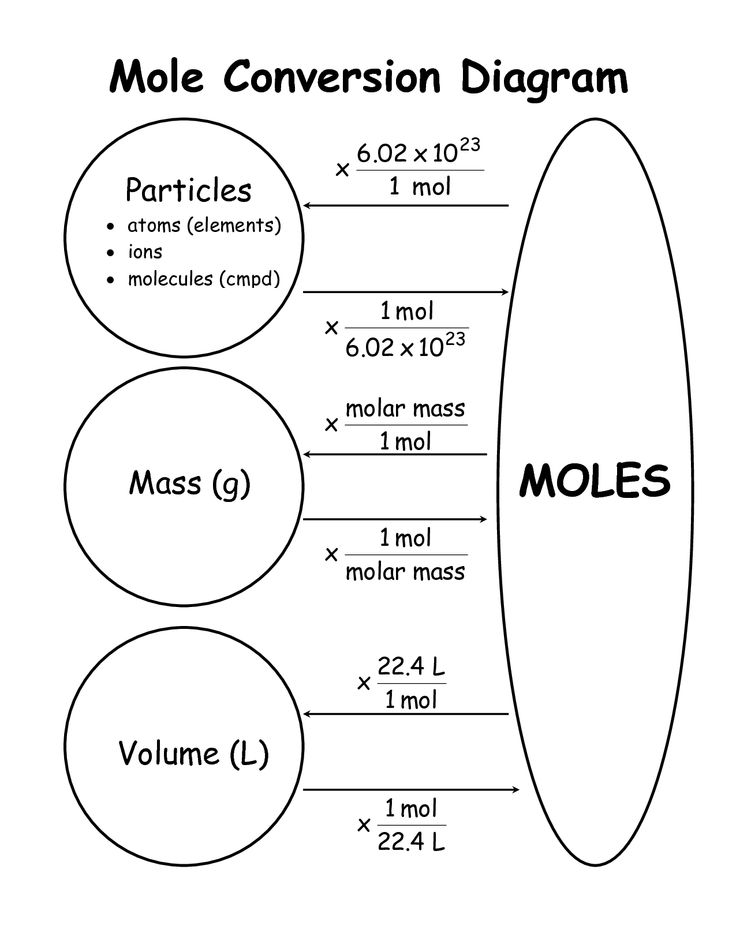
5 Easy Mole Conversion Problems Solved With Work

In the realm of chemistry, understanding the principles of moles is akin to having a universal translator for chemical quantities. Moles bridge the gap between the macroscopic, tangible world of substances we handle daily and the microscopic, atomic level where reactions occur. This article focuses on five easy mole conversion problems, providing a clear pathway to understanding and calculating moles in different scenarios. Whether you're a student grappling with stoichiometry or someone curious about how chemicals are measured, these problems will demystify mole conversions.
Problem 1: Converting Mass to Moles


Let’s start with a fundamental question:
Given 34 grams of sodium (Na), how many moles are there?
- Step 1: Find the atomic mass of sodium from the periodic table. Sodium (Na) has an atomic mass of approximately 22.99 g/mol.
- Step 2: Use the formula: [ \text{moles} = \frac{\text{mass}}{\text{atomic mass}} ]
- Step 3: Plug in the values: [ \text{moles} = \frac{34 \text{ grams}}{22.99 \text{ g/mol}} \approx 1.479 \text{ moles} ]
This approach works not just for atoms but also for molecules by considering their molecular mass.
📝 Note: Always ensure you use the most precise value for atomic masses available in your periodic table or reference material for accurate results.
Problem 2: Converting Moles to Mass

If you have 0.5 moles of calcium (Ca), what is its mass in grams?
- Step 1: Retrieve the atomic mass of calcium. Calcium (Ca) has an atomic mass of approximately 40.08 g/mol.
- Step 2: Apply the formula: [ \text{mass} = \text{moles} \times \text{atomic mass} ]
- Step 3: Calculate: [ \text{mass} = 0.5 \text{ moles} \times 40.08 \text{ g/mol} = 20.04 \text{ grams} ]
Problem 3: Moles from Gas Volume at STP


Determine the number of moles of oxygen gas (O2) at Standard Temperature and Pressure (STP) with a volume of 22.4 liters.
- Step 1: Understand that one mole of any ideal gas occupies 22.4 liters at STP.
- Step 2: Since O2 is diatomic, each molecule counts for two atoms, but gas law calculations do not directly depend on this fact here: [ \text{moles} = \frac{\text{volume (L)}}{22.4 \text{ L/mol}} ]
- Step 3: Plug in the values: [ \text{moles} = \frac{22.4 \text{ L}}{22.4 \text{ L/mol}} = 1 \text{ mole} ]
💡 Note: Ideal gas behavior at STP simplifies mole calculations, but real gases may deviate from these ideal conditions.
Problem 4: Moles in Compounds

What is the number of moles of hydrogen atoms in 2 moles of glucose (C6H12O6)?
- Step 1: Identify the molecular formula and count the hydrogen atoms in one glucose molecule. In C6H12O6, there are 12 hydrogen atoms.
- Step 2: Use the molar ratio to determine moles of hydrogen: [ \text{moles of hydrogen} = 2 \text{ moles of glucose} \times 12 \text{ hydrogen atoms per glucose molecule} ]
- Step 3: Calculate: [ \text{moles of hydrogen} = 24 \text{ moles} ]
Problem 5: Converting Avogadro’s Number


How many atoms are present in 0.75 moles of aluminum (Al)?
- Step 1: Use Avogadro’s number, which represents the number of entities in one mole: [ \text{Avogadro’s number} = 6.022 \times 10^{23} \text{ atoms/mol} ]
- Step 2: Multiply the moles by Avogadro’s number: [ \text{number of atoms} = 0.75 \text{ moles} \times 6.022 \times 10^{23} \text{ atoms/mol} ]
- Step 3: Compute: [ \text{number of atoms} \approx 4.5165 \times 10^{23} \text{ atoms} ]
The beauty of mole conversions lies in their ability to link the measurable world with the atomic and molecular realms. Understanding moles provides chemists and students alike with a critical tool for quantifying reactions, making predictions, and understanding the atomic nature of matter. From these basic calculations, one can venture into stoichiometry, reaction balancing, and even more complex chemical applications.
Why do we use moles in chemistry?

+
Moles are a fundamental unit in chemistry that allows us to count atoms, molecules, or ions in a way that’s scalable from the microscopic to the macroscopic level. They are crucial for understanding and quantifying chemical reactions, ensuring accurate stoichiometry, and simplifying complex calculations in chemical equations.
What is the difference between molar mass and atomic mass?

+
Atomic mass refers to the mass of a single atom of an element in atomic mass units (amu), while molar mass is the mass of one mole of a substance in grams per mole (g/mol). Molar mass incorporates atomic mass but is the sum of all atoms’ masses in a molecule, adjusted for the proportions in which they exist in a compound.
How do temperature and pressure affect gas calculations?

+
Temperature and pressure can significantly affect gas calculations because they alter the volume a gas occupies. At Standard Temperature and Pressure (STP), these variables are standardized to simplify calculations. However, real gases under different conditions can deviate from ideal gas law predictions due to molecular interactions.
Can you have a fraction of a mole?
+
Yes, a fraction of a mole is quite common in chemistry. It represents a proportion of Avogadro’s number of entities, whether atoms, molecules, or ions. For instance, 0.5 moles of any substance still contains half of Avogadro’s number of particles, maintaining the principle of counting at the molecular level.