Mixed Numbers to Improper Fractions: Free Worksheet

Understanding how to convert mixed numbers to improper fractions is a fundamental math skill that builds a strong foundation for more complex arithmetic. Whether you're preparing for a math test, helping a student with homework, or just refreshing your own knowledge, this process is both simple and practical. In this guide, we will walk through the steps to convert mixed numbers into improper fractions, provide examples, and offer a worksheet for practice.
The Basics of Mixed Numbers and Improper Fractions
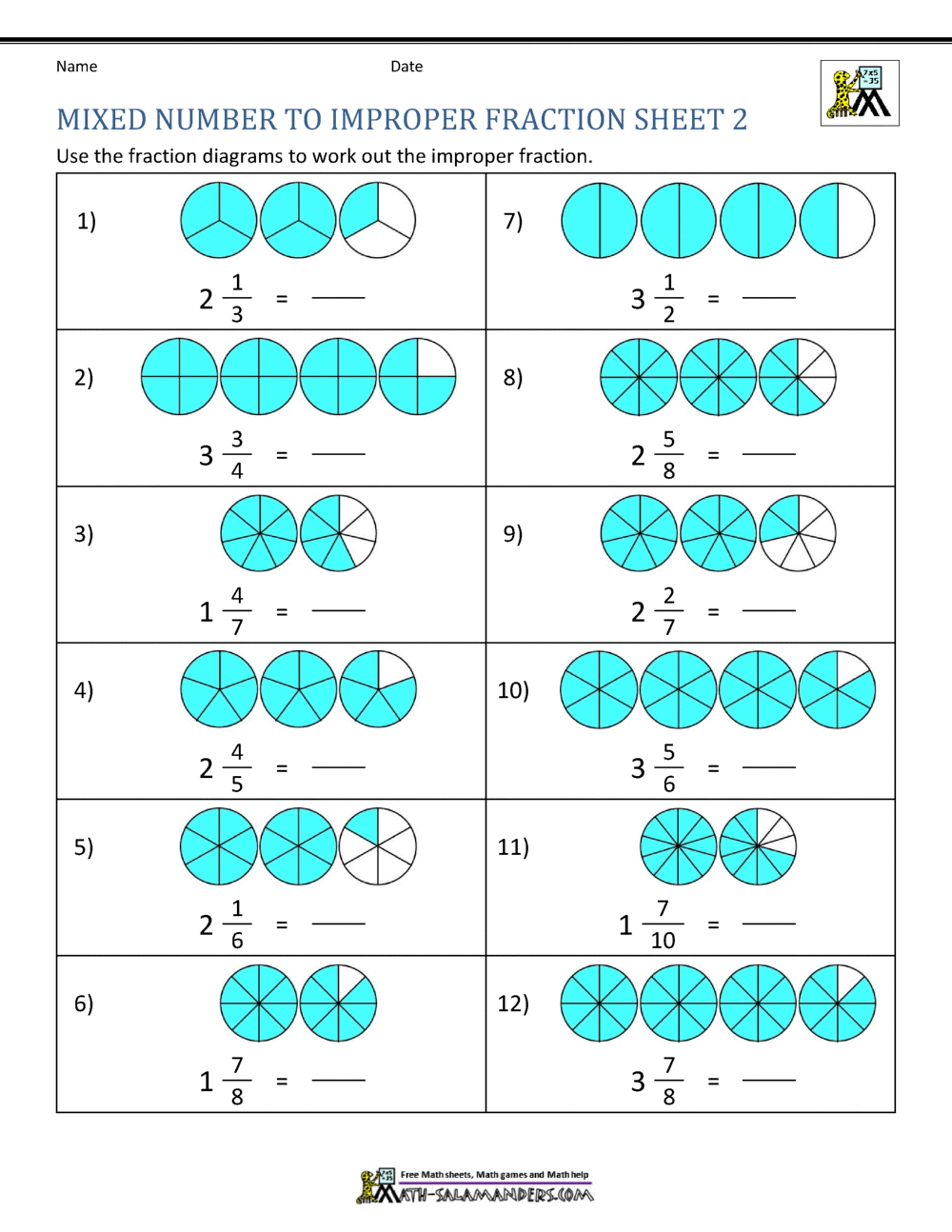

A mixed number is a combination of a whole number and a proper fraction (less than one). For instance, 3 1⁄2 is a mixed number where 3 is the whole number and 1⁄2 is the fraction part. On the other hand, an improper fraction is a fraction where the numerator is greater than or equal to the denominator, like 5⁄2.
Step-by-Step Conversion Process

- Step 1: Identify the Whole Number
Let’s take the mixed number 3 1⁄2 as an example. The whole number here is 3.
- Step 2: Multiply the Whole Number by the Denominator
Here, we multiply 3 (the whole number) by 2 (the denominator of the fraction part). This gives us 6.
- Step 3: Add the Numerator
We add the numerator from the fractional part (1) to the result from Step 2 (6). This sum gives us 7.
- Step 4: Place the Sum over the Original Denominator
Now, we have the improper fraction with the numerator 7 and the denominator 2, which is 7⁄2.
Let’s Practice with Examples

Here are a few examples to solidify your understanding:
- Example 1: Convert 2 3⁄4 to an improper fraction.
- Whole number (2) × Denominator (4) = 8
- 8 + Numerator (3) = 11
- Answer: 11⁄4
- Example 2: Convert 5 2⁄3 to an improper fraction.
- Whole number (5) × Denominator (3) = 15
- 15 + Numerator (2) = 17
- Answer: 17⁄3
💡 Note: Remember, the key to conversion is multiplication and addition!
Conversion Worksheet

Practice makes perfect, and here’s a worksheet to help you cement this skill:
| Mixed Number | Improper Fraction |
|---|---|
| 1 1/2 | ___/___ |
| 2 2/3 | ___/___ |
| 4 1/4 | ___/___ |
| 3 3/5 | ___/___ |
| 5 1/3 | ___/___ |

In summary, converting mixed numbers to improper fractions involves a straightforward process of multiplication and addition. This skill not only enhances your understanding of fractions but also facilitates solving more complex mathematical problems. The provided worksheet will help you practice until the conversion becomes second nature. Keep practicing to make this math operation intuitive.
Why do we convert mixed numbers to improper fractions?
+
Converting mixed numbers to improper fractions simplifies arithmetic operations like addition, subtraction, division, and even solving algebra equations involving fractions. It makes the calculation more uniform, reducing the need for separate operations on whole numbers and fractions.
Can improper fractions always be converted back to mixed numbers?

+
Yes, an improper fraction can be converted back into a mixed number by dividing the numerator by the denominator. The quotient will be the whole number, and the remainder will be the numerator of the fraction, with the original denominator unchanged.
Are improper fractions and mixed numbers equivalent in value?

+
Absolutely. Converting between mixed numbers and improper fractions doesn’t change the value of the number; it only changes the way it is represented mathematically.