5 Ways to Master Mixed Fractions with Worksheets

Understanding Mixed Fractions: A Comprehensive Guide

Mixed fractions are a fundamental concept in mathematics that can be challenging for students to grasp. A mixed fraction is a combination of a whole number and a proper fraction. For instance, 2 1⁄2 is a mixed fraction that represents 2 whole units and 1⁄2 of another unit. Mastering mixed fractions is essential for solving various mathematical problems, and with the right approach, students can develop a deep understanding of this concept.
Breaking Down Mixed Fractions

To understand mixed fractions, it’s essential to break them down into their components. A mixed fraction consists of three parts:
- Whole number: The whole number part represents the number of complete units.
- Numerator: The numerator is the number of equal parts that the whole is divided into.
- Denominator: The denominator represents the total number of equal parts that the whole is divided into.
For example, in the mixed fraction 3 3⁄4, 3 is the whole number, 3 is the numerator, and 4 is the denominator.
Method 1: Visualizing Mixed Fractions

One effective way to master mixed fractions is to visualize them using real-life objects or diagrams. For instance, consider a pizza that is divided into 8 equal slices. If you eat 3 slices, you can represent this as a mixed fraction: 3 3⁄8. This visualization technique helps students understand the concept of mixed fractions and how they can be used to represent real-world problems.
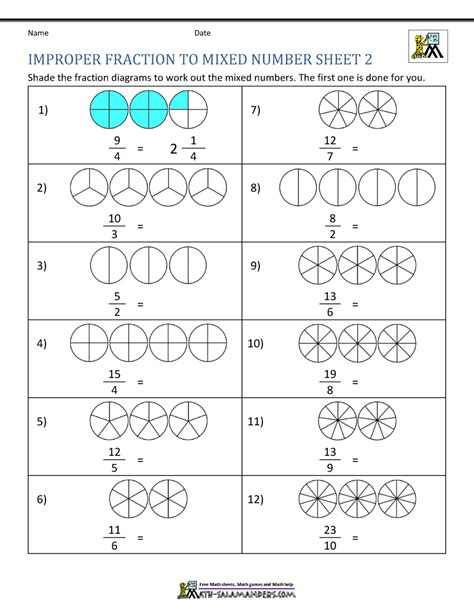
Method 2: Converting Improper Fractions to Mixed Fractions

Another method to master mixed fractions is to convert improper fractions to mixed fractions. An improper fraction is a fraction where the numerator is greater than the denominator. To convert an improper fraction to a mixed fraction, you need to divide the numerator by the denominator and find the remainder.
For example, consider the improper fraction 11⁄4. To convert this to a mixed fraction, divide 11 by 4, which gives you 2 with a remainder of 3. Therefore, the mixed fraction equivalent of 11⁄4 is 2 3⁄4.
Method 3: Adding and Subtracting Mixed Fractions
Adding and subtracting mixed fractions is another essential skill that students need to master. To add or subtract mixed fractions, you need to follow these steps:
- Add or subtract the whole number parts.
- Add or subtract the fraction parts.
- Simplify the fraction parts, if necessary.
For example, consider the following problem: 2 1⁄2 + 1 3⁄4. To solve this problem, add the whole number parts: 2 + 1 = 3. Then, add the fraction parts: 1⁄2 + 3⁄4 = 5⁄4. Finally, simplify the fraction part: 5⁄4 = 1 1⁄4. Therefore, the answer is 3 1 1⁄4 + 1 3⁄4 = 4 2 1⁄4.
Method 4: Multiplying and Dividing Mixed Fractions

Multiplying and dividing mixed fractions is another critical skill that students need to master. To multiply mixed fractions, follow these steps:
- Convert the mixed fractions to improper fractions.
- Multiply the numerators and denominators.
- Simplify the resulting fraction, if necessary.
For example, consider the following problem: 2 1⁄2 × 3 3⁄4. To solve this problem, convert the mixed fractions to improper fractions: 2 1⁄2 = 5⁄2 and 3 3⁄4 = 15⁄4. Then, multiply the numerators and denominators: 5⁄2 × 15⁄4 = 75⁄8. Finally, simplify the resulting fraction: 75⁄8 = 9 3⁄8.
Method 5: Using Mixed Fraction Worksheets

Finally, using mixed fraction worksheets is an excellent way to practice and reinforce students’ understanding of mixed fractions. Worksheets provide a variety of problems that cater to different learning styles and abilities. By practicing with worksheets, students can develop their problem-solving skills and build their confidence in working with mixed fractions.
📝 Note: You can find a variety of mixed fraction worksheets online that cater to different grade levels and learning styles.
In conclusion, mastering mixed fractions requires a combination of understanding, visualization, and practice. By using the methods outlined above, students can develop a deep understanding of mixed fractions and become proficient in solving problems that involve this concept.
What is a mixed fraction?

+
A mixed fraction is a combination of a whole number and a proper fraction. For example, 2 1⁄2 is a mixed fraction that represents 2 whole units and 1⁄2 of another unit.
How do I convert an improper fraction to a mixed fraction?

+
To convert an improper fraction to a mixed fraction, divide the numerator by the denominator and find the remainder. The quotient is the whole number part, and the remainder is the numerator of the fraction part.
How do I add or subtract mixed fractions?

+
To add or subtract mixed fractions, add or subtract the whole number parts, add or subtract the fraction parts, and simplify the fraction parts, if necessary.
Related Terms:
- Mixed fractions worksheets pdf
- Mixed fractions worksheets with answers
- Fractions worksheets with answers PDF
- Multiplying fractions worksheets
- Free mixed fractions worksheets