5 Simple Steps to Convert Mixed Fractions to Improper Fractions

Converting mixed fractions to improper fractions might seem daunting initially, but with a clear understanding and the right approach, it can become straightforward. This conversion is not only a fundamental skill in mathematics but also essential for simplifying algebraic expressions, solving equations, and understanding ratios in more complex mathematical contexts. Here are five simple steps to help you master the conversion of mixed fractions to improper fractions effectively.
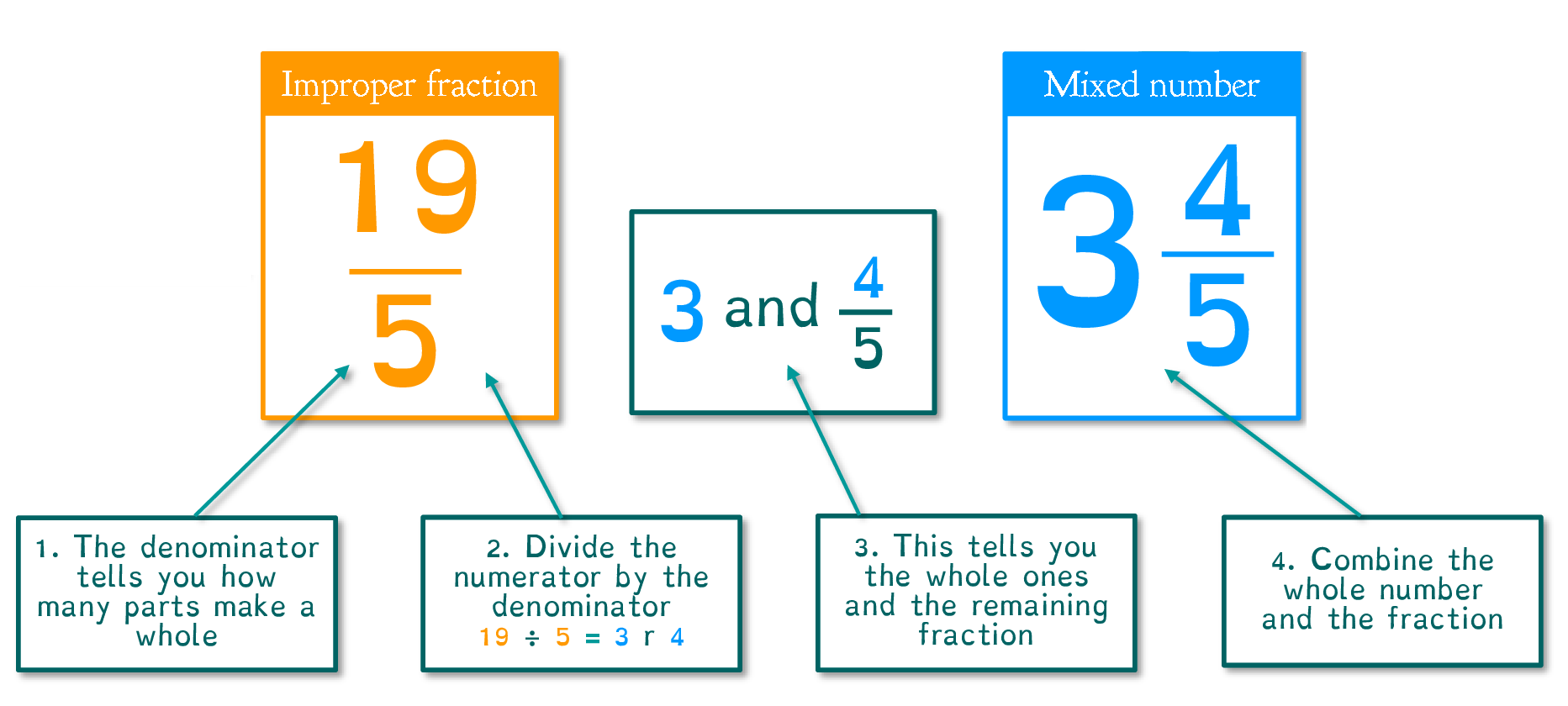
Understanding Mixed and Improper Fractions

Before delving into the conversion process, let's define what we mean by mixed fractions and improper fractions:
- Mixed Fraction: This consists of a whole number combined with a proper fraction (e.g., 1 2/3, where 1 is the whole number and 2/3 is the fraction).
- Improper Fraction: Here, the numerator is equal to or greater than the denominator (e.g., 5/3, where 5, the numerator, is greater than 3, the denominator).
Step 1: Identifying the Components

The first step in converting a mixed fraction to an improper fraction is to identify its components:
- The whole number part
- The numerator of the fractional part
- The denominator of the fractional part
For example, in 2 3/4:
- 2 is the whole number
- 3 is the numerator
- 4 is the denominator
Step 2: Multiply the Whole Number by the Denominator

Take the whole number and multiply it by the denominator of the fractional part. This step essentially converts the whole number into the same fractional units as the numerator of the fraction:
- 2 x 4 = 8
⚠️ Note: Remember to keep the denominator from the original fraction.
Step 3: Add the Numerator to the Result

Now, take the product from Step 2 and add it to the numerator of the fractional part:
- 8 + 3 = 11
Step 4: Form the Improper Fraction

Combine the new numerator (from Step 3) with the original denominator to form your improper fraction:
- New Numerator: 11
- Denominator: 4
The resulting improper fraction is 11⁄4.
Step 5: Simplification (Optional)

Although not mandatory, you can simplify the improper fraction if possible. To simplify, you’ll divide both the numerator and the denominator by their greatest common divisor (GCD):
- For 11⁄4, the GCD is 1, so it remains unchanged.
Now that we've walked through the process, let's summarize the conversion with a table:
| Step | Description | Example (2 3/4) |
|---|---|---|
| 1 | Identify Components | Whole Number: 2, Numerator: 3, Denominator: 4 |
| 2 | Multiply Whole Number by Denominator | 2 x 4 = 8 |
| 3 | Add Result to Numerator | 8 + 3 = 11 |
| 4 | Form Improper Fraction | 11/4 |
| 5 | Simplify (if possible) | 11/4 (unchanged) |

Converting mixed fractions to improper fractions is a core arithmetic skill that aids in solving more complex mathematical problems. Understanding this conversion opens up numerous applications in algebra, physics, and beyond. Through these five steps, you now have a methodical approach to perform this conversion with confidence and ease.
Why convert mixed fractions to improper fractions?

+
Converting mixed fractions to improper fractions allows for easier manipulation in mathematical operations like addition, subtraction, multiplication, and division, as well as in solving equations or working with rational expressions.
Can an improper fraction be simplified further?

+
Yes, if the numerator and denominator share common factors other than 1, you can simplify the fraction by dividing both by their greatest common divisor.
Is it necessary to simplify improper fractions?
+
While simplification is not strictly necessary for every problem, it does make the fraction easier to work with and interpret, especially in further calculations or comparisons.