5 Ways to Solve Missing Angles Fast

Geometry can often present puzzles that test not just our knowledge of shapes and properties but also our ability to solve problems quickly and accurately. Among these challenges, finding missing angles in various geometric figures is quite common. Today, we will explore five efficient techniques to solve missing angles faster, making geometry not just manageable but also fun.
Understanding Basic Geometric Properties

Before diving into the methods, let’s establish some basic geometric properties:
- Sum of angles in a triangle: The total of all interior angles equals 180°.
- Angles around a point: The sum of all angles at a single point is 360°.
- Complementary angles: Two angles whose measures add up to 90°.
- Supplementary angles: Two angles whose measures add up to 180°.
📐 Note: Knowing these properties by heart will significantly speed up your angle calculations.
Method 1: Using Triangle Sum Property

The simplest way to find a missing angle in a triangle is by using the fact that the sum of its interior angles is always 180°:
- Identify two known angles.
- Subtract the sum of these two angles from 180° to get the third angle.

Let’s say, if in triangle ABC, ∠A = 30° and ∠B = 50°, then:
- Missing angle © = 180° - (30° + 50°) = 100°
Method 2: Utilizing Parallel Lines

When you’re dealing with angles formed by parallel lines and a transversal:
- If two lines are parallel, corresponding angles are equal.
- Alternate interior angles are also equal.
- Same-side interior angles are supplementary (add up to 180°).

Example: Given ∠F = 60°, since F is corresponding to G, we know ∠G also equals 60°.
Method 3: Applying the Exterior Angle Theorem

This theorem is particularly useful in problems involving triangles with external angles:
- The measure of an exterior angle of a triangle is equal to the sum of the two non-adjacent interior angles.
If ∠A and ∠B are the non-adjacent interior angles to an exterior ∠X, then:
- ∠X = ∠A + ∠B
Method 4: Using Angle Bisectors
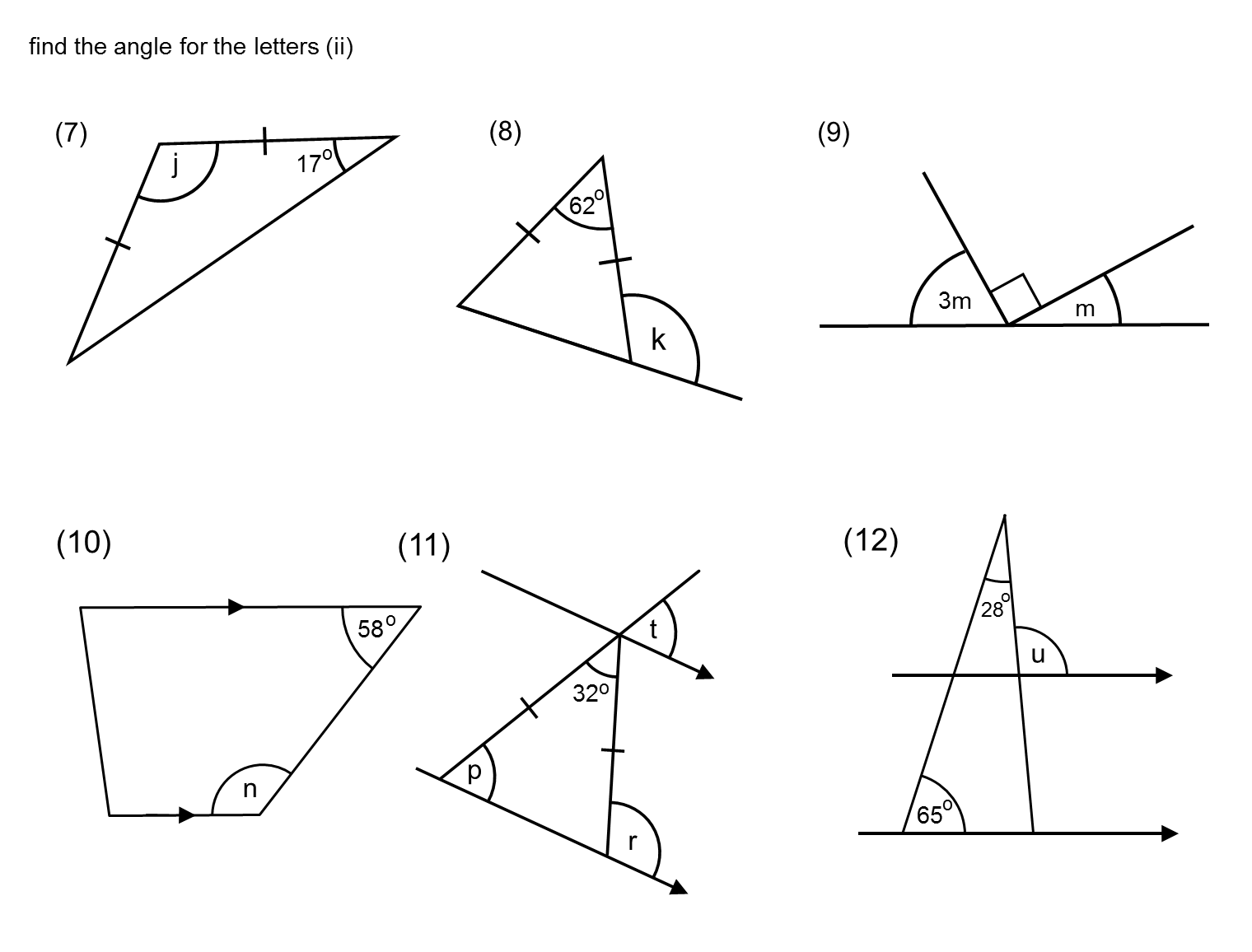
An angle bisector divides an angle into two equal smaller angles. Here’s how you can use it to find missing angles:
- If you know one part of an angle, divide it by 2 to find the bisector angle.
- Use this to calculate or confirm other angles in the figure.

If ∠P = 90° and it’s bisected, each angle will be 45°.
Method 5: Employing Polygons

For figures other than triangles, we can use the formula for the sum of interior angles of a polygon:
- Sum of Interior Angles = 180° (n - 2), where n is the number of sides.
Once you know the sum, divide by the number of angles to find each interior angle, or subtract known angles from the sum to find the unknown one.
Here’s an example for a pentagon (n=5):
- Sum = 180° (5 - 2) = 540°
- If four angles are 110°, 90°, 130°, and 110°, the missing angle would be 540° - (110° + 90° + 130° + 110°) = 100°.
To sum up these techniques, mastering these methods will not only make solving for missing angles easier but will also enhance your overall geometric reasoning skills. Geometry, with its precise rules and relationships, becomes less daunting when you have these tools in your mental toolkit.
What if I encounter a shape I don’t know how to solve?
+
When you encounter an unfamiliar shape, break it down into known shapes, or look for symmetrical or repeating patterns that can simplify the problem.
Can these methods apply to 3D shapes as well?

+
Yes, many of these methods can be extended to 3D shapes. For example, the sum of angles in a pyramid’s base will still add up to 180° if it’s triangular, or you can use projections to solve problems.
How accurate do these methods need to be?
+
These methods provide theoretical solutions; however, in practical applications, consider the precision required. For example, in construction or navigation, rounding and measurement errors must be accounted for.