Solve the Missing Angle Puzzle: Worksheet Answers Revealed

Understanding angles and their relationships within triangles is a fundamental aspect of geometry. Whether you are a student striving to conquer your geometry homework, or a teacher looking to assist your students, this long-form guide will walk you through the process of solving puzzles involving missing angles. In this post, we'll reveal answers for a typical worksheet focused on this intriguing topic.
Basic Principles of Triangles and Angles

Before diving into the worksheet answers, let's establish some ground rules:
- Sum of Angles in a Triangle: The sum of all interior angles in a triangle is always 180°.
- Isosceles Triangles: If a triangle has at least two equal sides, it has at least two equal angles.
- Equilateral Triangles: All sides and angles are equal (60°).
Types of Triangles and Their Angles

Here's a brief overview:
| Triangle Type | Properties |
|---|---|
| Scalene | All sides and angles are different. |
| Isosceles | Two sides and their opposite angles are equal. |
| Equilateral | All sides and angles are equal to 60°. |
| Right Triangle | Contains one 90° angle. |

Solving for Missing Angles in Triangles

To solve for missing angles, use the principles above:
- Identify the type of triangle if possible.
- Apply the sum of angles rule for a triangle.
- Use any given angles to find the missing ones.
Worksheet Example #1:
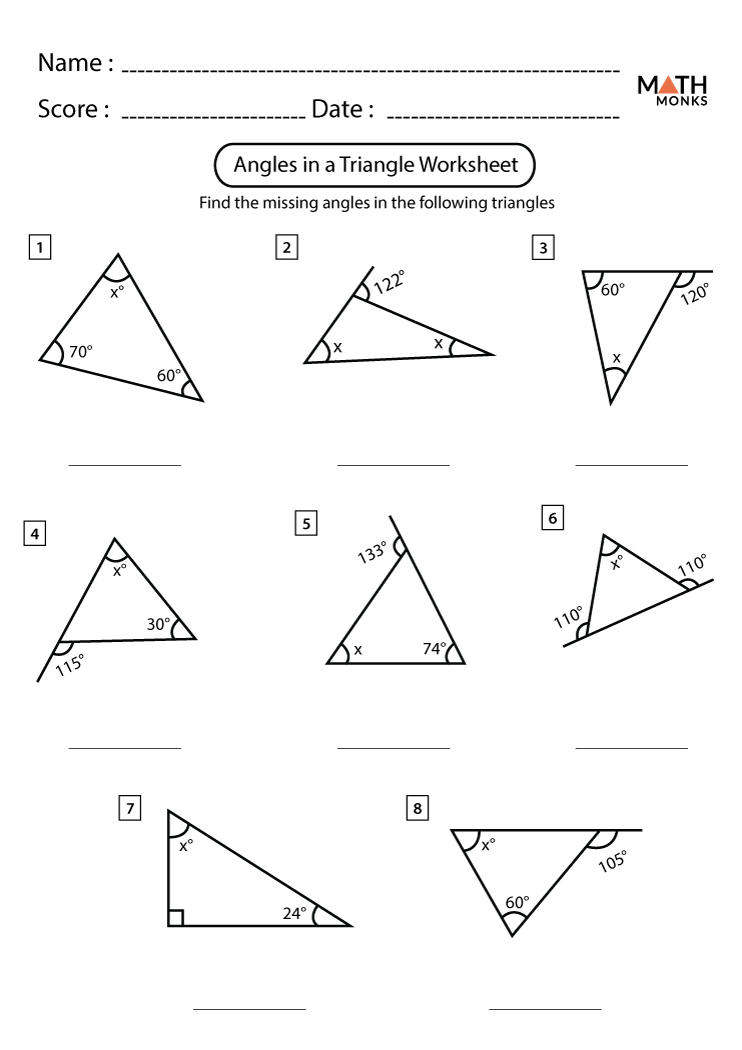
Find the missing angle x in a triangle where two angles are 50° and 70°.
- Step 1: Sum of angles = 180°
- Step 2: Solve for x: 180° - 50° - 70° = 60°
📐 Note: Make sure to label the triangle's sides and angles clearly on your worksheet for easy reference.
Worksheet Example #2:

In an isosceles triangle, one base angle is 45°, what are the other angles?
- Step 1: If the triangle is isosceles, the two base angles are equal.
- Step 2: x + x + 45° = 180°
- Step 3: Solve for x: 2x + 45° = 180°, so 2x = 135°, x = 67.5°
By understanding these basic principles and following the steps, you'll be able to tackle even the trickiest of missing angle problems. Remember to always double-check your work to avoid common errors like forgetting to account for all angles or mislabeling angles.
Further Considerations

When dealing with complex triangles or when angles need to be found in sets of triangles:
- Use exterior angle theorems, which state that the exterior angle equals the sum of the two non-adjacent interior angles.
- Apply the angle sum property of polygons when triangles are part of larger figures.
🔹 Note: Sometimes a problem may require you to solve for an angle in a larger shape by considering it as a combination of triangles.
Worksheet Answers Summary
In closing, by applying the principles of angles in triangles, we’ve successfully navigated through common puzzles encountered in geometry worksheets. Here’s a quick summary:
- The sum of the interior angles of any triangle is 180°.
- Isosceles and equilateral triangles provide shortcuts in solving for angles due to their symmetrical properties.
- Exterior angles and angle sums in polygons can also be vital in solving complex problems.
Embrace these core concepts, practice them, and you’ll find yourself solving missing angle puzzles with ease.
Can all angles in a triangle be acute?

+
Yes, all angles in a triangle can be acute, forming an acute triangle.
What is the difference between an exterior and interior angle?
+
An exterior angle of a triangle is formed by one side of the triangle and the extension of an adjacent side, whereas an interior angle is the angle inside the triangle at any vertex.
What is a supplementary angle?

+
Supplementary angles are two angles whose measures add up to 180°. In a triangle, the exterior angle is supplementary to the adjacent interior angle.