Midpoint of Line Segment: Engaging Worksheet with Answers

In the study of geometry, one of the foundational concepts is understanding how to find the midpoint of a line segment. This skill is not just a stepping stone for students learning coordinate geometry; it is pivotal in real-world applications like engineering, navigation, and even animation. This worksheet is designed to engage students in exploring the concept of the midpoint through a series of exercises, discussions, and visual aids.
Understanding Midpoints

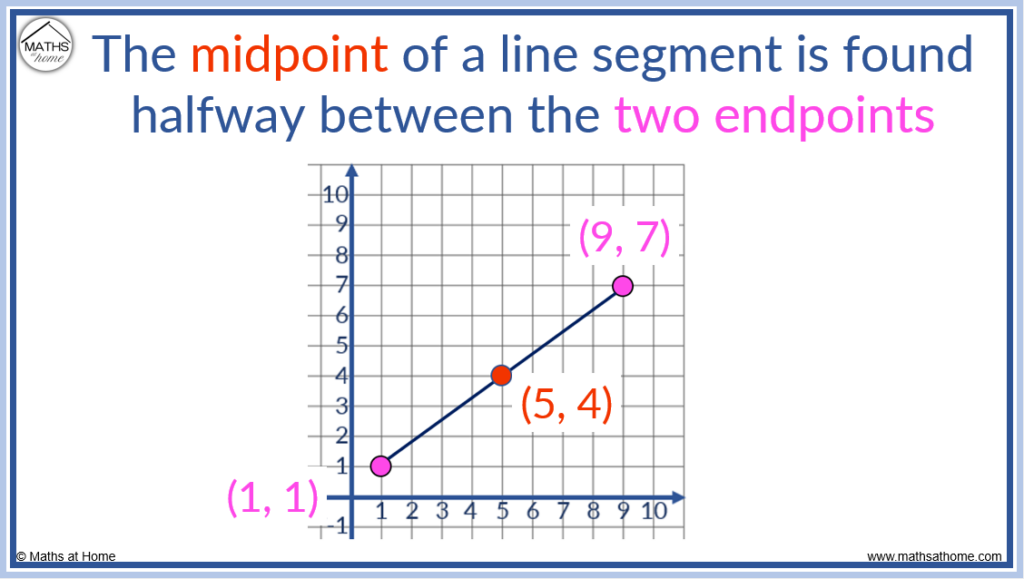
Let’s start by defining what a midpoint is. The midpoint of a line segment is the point exactly halfway between the segment’s endpoints. If you have two points, (A(x_1, y_1)) and (B(x_2, y_2)), the formula to find the midpoint (M) is:
M = \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right)Here's a visual representation:
🌐 Note: This image is for illustrative purposes; actual placement of images should be right after primary headings.
Interactive Exercises

Below are several exercises to help you practice calculating the midpoints:
Exercise 1: Basic Calculation
Find the midpoint of a line segment with endpoints at (2, 3) and (6, 9).
Steps:
- Identify the coordinates: A(2, 3) and B(6, 9)
- Use the formula for the midpoint M: \[ M = \left( \frac{2 + 6}{2}, \frac{3 + 9}{2} \right) \]
- Calculate the x and y coordinates for the midpoint: \[ M = \left( \frac{8}{2}, \frac{12}{2} \right) = (4, 6) \]
Exercise 2: Algebraic Expression

Given points A(a, b) and B(c, d), find the midpoint M in terms of variables.
Solution:
- The midpoint M will be: \[ M = \left( \frac{a + c}{2}, \frac{b + d}{2} \right) \]
Exercise 3: Solving for Endpoint

If the midpoint of a segment is (1, 1) and one endpoint is (4, 5), what are the coordinates of the other endpoint?
Steps:
- Let the unknown endpoint be C(x, y).
- The midpoint formula gives us two equations: \[ 1 = \frac{4 + x}{2} \quad \text{and} \quad 1 = \frac{5 + y}{2} \]
- Solving these equations: \[ 4 + x = 2 \Rightarrow x = 2 - 4 = -2 \] \[ 5 + y = 2 \Rightarrow y = 2 - 5 = -3 \]
- Therefore, the other endpoint is (-2, -3).
| Exercise | Endpoint A | Endpoint B | Midpoint |
|---|---|---|---|
| 1 | (2, 3) | (6, 9) | (4, 6) |
| 2 | (a, b) | (c, d) | ( \frac{a + c}{2}, \frac{b + d}{2} ) |
| 3 | (4, 5) | Unknown | (1, 1) |

💡 Note: This table summarizes the results from our exercises, aiding in quick reference.
Visual and Conceptual Understanding

Visual aids can significantly enhance understanding. Here are some insights:
- Geometric Meaning: The midpoint divides a line segment into two equal parts. This can be visualized by folding a straight line in half where the fold line represents the midpoint.
- Vector Interpretation: The midpoint can also be seen as the average of two vectors pointing to the endpoints, which leads to discussions about vector addition in higher-level math.
Practical Applications

Midpoints have numerous applications:
- Computer Graphics: When drawing lines in digital art or game development, understanding midpoints helps in implementing algorithms like the midpoint circle algorithm or line-drawing algorithms.
- Navigation: GPS systems often use midpoint calculations to find the center point between multiple locations for efficient route planning.
To summarize, finding the midpoint of a line segment is a simple yet powerful concept in geometry, with applications ranging from coordinate algebra to advanced graphics programming. Through these exercises, you've not only practiced calculating midpoints but also explored the geometry's visual and conceptual aspects. This understanding equips you to solve more complex problems in your mathematical journey and to think more critically about spatial relationships.
Why is finding the midpoint of a line segment important?

+
Understanding midpoints is crucial for applications in coordinate geometry, computer graphics, navigation, and more, where dividing a line or space into equal parts is necessary for calculations and design.
Can you find the midpoint of a line segment in 3D space?

+
Yes, the formula extends to 3D with ( M = \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}, \frac{z_1 + z_2}{2} \right) ).
What if one endpoint of a segment is unknown?

+
You can use the midpoint formula to solve for the unknown endpoint, as shown in Exercise 3.
