Midpoint and Distance Formula Worksheet Answers: 5 Essential Tips

In the realm of mathematics, especially in geometry, understanding how to calculate distances and midpoints between two points is foundational. This blog post explores the Midpoint and Distance Formula worksheet answers, offering five essential tips to improve your grasp on these crucial concepts. Whether you're a student, teacher, or math enthusiast, these insights will provide clarity and facilitate a deeper understanding of coordinate geometry.
Understanding the Basics of Midpoint and Distance Formulas

Before we delve into our essential tips, let’s recap the fundamental formulas:
- Distance Formula: The distance d between two points ((x_1, y_1)) and ((x_2, y_2)) is given by:
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}- Midpoint Formula: The midpoint M of a line segment with endpoints ((x_1, y_1)) and ((x_2, y_2)) is:
M = \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right)
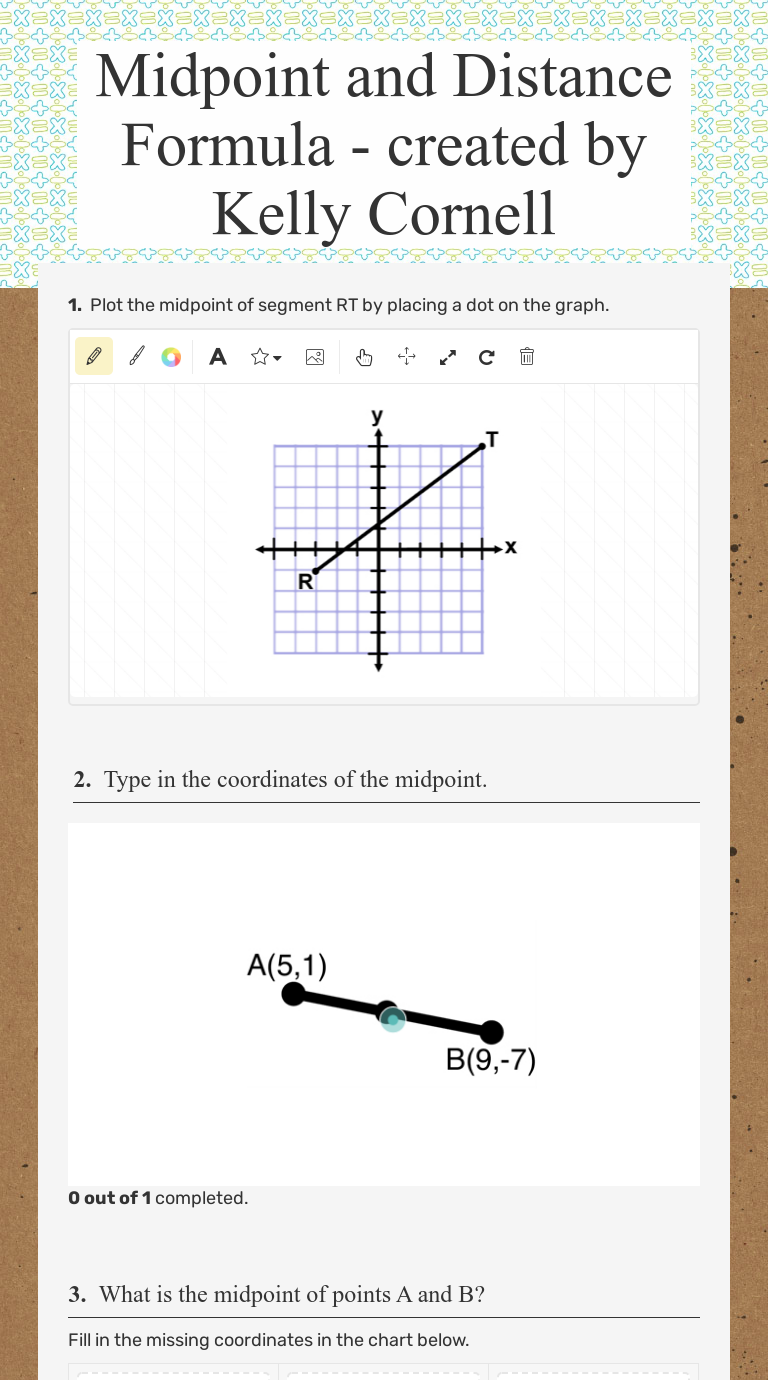
Tip 1: Visualize the Coordinate Grid


Visualizing the problem on a coordinate plane can make calculations more intuitive:
- Plot the given points on a grid.
- Observe how the distance forms a right triangle, where the distance is the hypotenuse.
- Draw lines to connect the points and the midpoint to better conceptualize the relationships.
Tip 2: Simplify Your Calculations

When finding distances, especially in problems where large numbers are involved:
- Consider rounding to the nearest whole number if the final result requires it.
- Use the Pythagorean theorem directly to estimate distances before applying the formula.
- Pay attention to the signs of coordinates to avoid unnecessary errors in algebraic manipulation.
Tip 3: Practice with Real-World Scenarios

Applying these formulas to real-world scenarios can enhance your understanding:
- Calculate the distance between two cities on a map.
- Determine the midpoint of a journey between two landmarks.
- Use coordinates in sports to analyze player movements or ball trajectory.
🎨 Note: Incorporating real-life applications helps in contextualizing mathematical concepts, making them easier to remember.
Tip 4: Use Technology for Validation

Modern technology provides tools to verify calculations:
- Graphing calculators or software like GeoGebra can visualize and calculate distances/midpoints.
- Use online distance calculators to check your work.
- Try different online platforms to understand different teaching methods.
Tip 5: Breakdown the Steps for Complex Problems

Complex problems often involve several steps. Here’s a table to guide you through breaking down these steps:
| Step | Description |
|---|---|
| 1. Identify Points | Clearly label the coordinates of the points given in the problem. |
| 2. Calculate Differences | Find the difference in x and y coordinates for distance calculation. |
| 3. Apply Formula | Use either the distance or midpoint formula based on the question’s requirement. |
| 4. Simplify | Perform algebraic manipulations, simplifying as much as possible. |
| 5. Solve | Finalize the calculation to obtain the distance or midpoint coordinates. |

Breaking down problems into these steps not only makes them manageable but also reduces the chance of errors.
By following these essential tips, you're well on your way to mastering the midpoint and distance formula concepts. Remember, consistent practice, visualization, real-world application, and validation through technology are key to deepening your understanding. Mathematics, particularly in areas like coordinate geometry, isn't just about memorizing formulas; it's about understanding the logic and beauty behind each calculation. Keep exploring, practicing, and applying these tips to solidify your knowledge.
What are the common mistakes students make with midpoint and distance formulas?
+
Students often confuse the signs when subtracting coordinates, forget to square the differences before summing them, or miss out on simplifying the square root or fractions properly.
How can I remember the formulas better?

+
Linking the formulas to visual or real-life contexts, such as the Pythagorean theorem for distance, helps in memorizing. Also, practicing them in different scenarios strengthens memory.
Is there any shortcut for calculating distances?

+
While there’s no universal shortcut, if points form a right angle or lie on the same axis, simpler methods like direct subtraction can be used, but always ensure these shortcuts are valid for the problem at hand.
How do these formulas help in navigation?

+
These formulas are the basis for calculating distances in GPS navigation systems, helping to find the shortest path between locations or the midpoint of a journey for stops.