5 Fun Ways to Measure Angles in Triangles

The Practical Art of Measuring Angles

Measuring angles in triangles is not only a fundamental part of geometry but also an engaging way to learn about shapes, symmetry, and balance. Whether you’re a student trying to understand the basics, an enthusiast exploring mathematical art, or a professional needing precision, there are several fun methods to make this learning process both effective and entertaining. Here are five creative ways to measure angles in triangles:
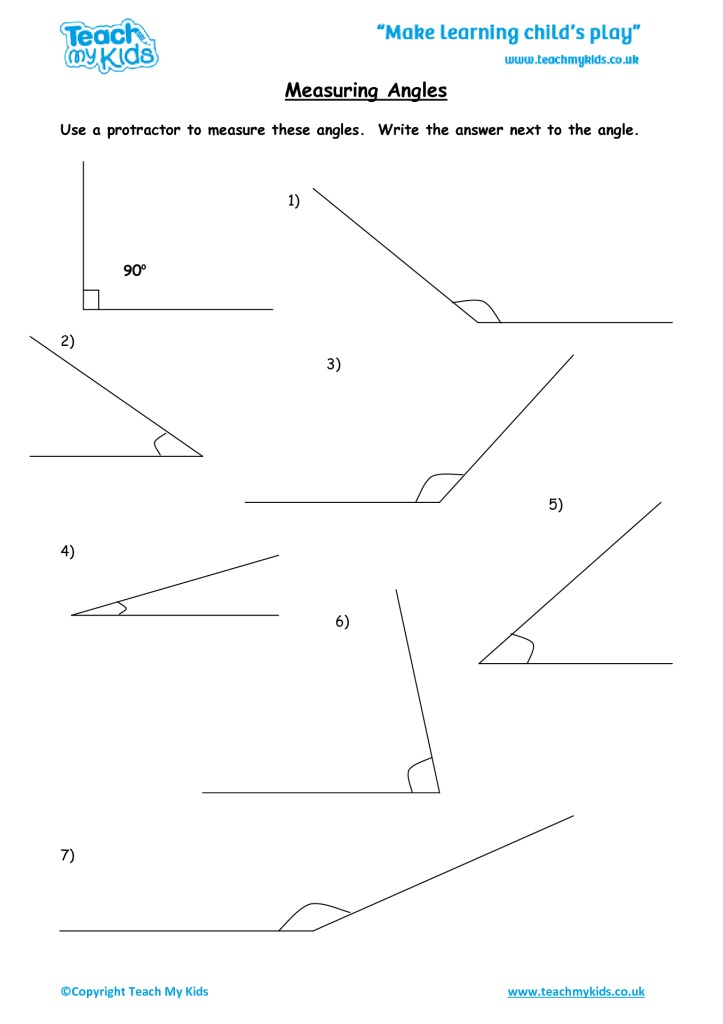
1. Using a Protractor
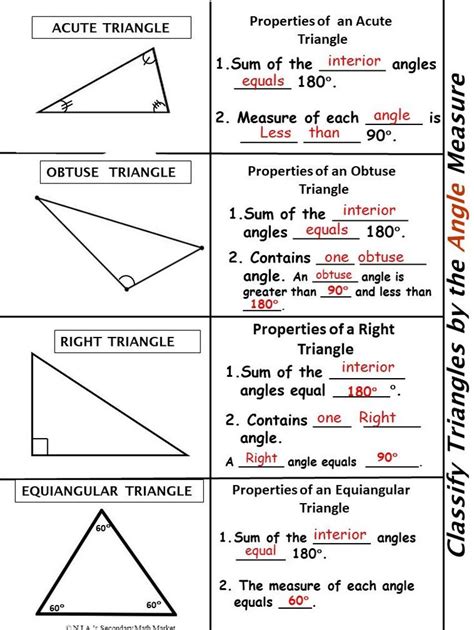
The traditional method for measuring angles in triangles is the use of a protractor. This tool is straightforward and effective for beginners:
- Step 1: Place the center of the protractor at one of the triangle’s vertices where two sides meet.
- Step 2: Align the protractor’s baseline with one of the sides of the triangle.
- Step 3: Read the angle where the other side crosses the protractor’s scale.
✏️ Note: Ensure the protractor is flat against the triangle to avoid mismeasurement.
2. Leveraging Paper or Sticks

For an interactive approach, you can use everyday items like paper or sticks:
- Paper Method: Fold the paper into an angle, cut along the fold line, and compare it to the angles in the triangle.
- Stick Method: Use three sticks to form a triangle. Measure angles by comparing their relative lengths.
| Method | Tools | Description |
|---|---|---|
| Paper | Origami or scrap paper | Fold, cut, and compare angles by matching paper edges. |
| Sticks | Small sticks or skewers | Form a triangle and estimate angles based on side lengths. |

3. Digital Apps and Software

Technology has made it easier to explore geometry with various apps and software:
- Geometry Apps: Use apps like GeoGebra or AngleBot to visualize and measure angles in 3D or virtual environments.
- Augmented Reality (AR): AR tools let you measure angles in real life by pointing your device’s camera at an object.
🌟 Note: Digital tools can make learning fun, but accuracy depends on calibration.
4. Constructing Angles with a Compass

For those who enjoy hands-on geometry, using a compass can be both educational and entertaining:
- Step 1: Fix the compass to a radius and draw an arc from the triangle’s vertex.
- Step 2: From the points where the arc intersects the sides, draw two more arcs with the same radius.
- Step 3: Connect the new points where the arcs intersect to create an angle bisector.
This method not only measures angles but also introduces the concept of angle bisectors.
5. Use of Gnomons or Sundials

Incorporating ancient methods, you can measure angles by observing shadows:
- Step 1: Use a gnomon (a straight vertical object) or sundial. Place it so that its shadow falls on the triangle.
- Step 2: Mark the point where the shadow touches one side of the triangle.
- Step 3: Measure the angle between the direction of the shadow and the sides of the triangle.
Wrapping Up the Geometric Exploration
Measuring angles in triangles is more than just a mathematical exercise; it’s a gateway to understanding spatial relationships, symmetry, and the art of shapes. Whether through traditional methods like a protractor, creative hands-on techniques using paper or sticks, or modern digital tools, each method brings its unique flavor to the learning experience. These techniques enhance visual literacy and encourage a deeper appreciation for geometry. As we’ve seen, from the precise measurements with compasses to the historical methods of gnomons, there’s a rich tapestry of approaches to explore.
This exploration not only enriches our knowledge but also instills a lifelong curiosity for the beauty in numbers and patterns. Triangles are ubiquitous in both nature and design, and understanding their angles can unlock a world of creativity and precision in your projects or explorations.
Why is measuring angles in triangles important?

+
Understanding angles in triangles allows for practical applications in fields like architecture, engineering, and design, where exact measurements are crucial for stability and balance.
How do I check the accuracy of my angle measurements?

+
Use multiple methods to cross-verify your measurements. Also, remember that the sum of the angles in any triangle should always be 180 degrees, providing an additional check for accuracy.
Can I measure angles in other shapes with these methods?

+
Absolutely, most of these methods can be adapted to measure angles in polygons or any geometric shapes, although some adjustments might be necessary for more complex figures.